RNN介绍及梯度详细推导
- 1. RNN简介
- 2. RNN的几种常见结构
- 结构一
- 结构二
- 结构三
- 3. RNN的梯度推导
1. RNN简介
RNN(Recurrent Neural Network, 循环神经网络)算得上是极具魅力的一类神经网络。同经典的前馈神经网络相比较(如多层感知器、深度置信网络、卷积神经网络等),RNN允许网络隐层(hidden layer)的输出再以输入的形式作用于该隐层自己。假设一个文本序列“I have a pen”,我们可以用一些方法将其中的每个单词进行向量化,如采用one-hot编码、ti-idf、词嵌入等方法。再假设我们有一个计算单元,它有两个输入。一个输入是上述提到的单词的向量,另一个输入是一个大小为m的向量。该计算单元的输出也是一个大小为m的向量。首先,我们随机初始化一个大小为m的向量,并将该向量和上述文本序列的第一个词“I”的词向量输入给计算单元。计算单元输出一个大小为m的向量。接着我们又将这个刚得到的大小为m的向量和第二个词“have”的向量输入给计算单元,又得到一个大小为m的向量。如此重复,直至对文本序列“I have a pen”进行了一次完整遍历,最终得到一个大小为m的向量。这个最终得到的向量就可以作为对原文本序列的一个表征,用于后续任务。例如,接一个输出层再加softmax用来做文本分类。
上述的计算单元有两个重要性质。首先,不论上述文本序列的长度如何变化,只要完成对该文本进行一次遍历,最终的输出向量大小均为m。因此它非常有利于处理不同长度的序列数据。其次,当前词总是伴随着前一个词的输出一起作为输入参与计算(递归),这就意味这序列本身的顺序能够被计算单元很好的捕捉到。因此,这样的计算单元特别适合于对序列顺序敏感的任务,如时序预测、词性标注等任务。
RNN的基本构成就是这样的计算单元。
从理论上看,RNN的一系列后续变体(如GRU、LSTM等)在设计上非常经验(实际上,必须承认目前大多数的网络在设计上都很经验),但却很容易被人们所接受。这些接受绝不仅仅是因为它们强大的性能表现,也包含其背后设计思路的“合理性”(符合直觉)。而经验式的合理,往往会催生大量后续更加“合理”的设计,这直接导致了一个研究领域的迅速崛起。RNN是这样,CNN是这样,Deep Learning也是这样。从实践上看,RNN在涉及到序列或自然语言的任务上获得了前所未有的成功,圈粉无数。本文的目的是详细介绍RNN的梯度推导过程,便于读者对RNN形成更加理性的认识。在正式进入推导之前,先简单介绍一下RNN的三种常见结构。
2. RNN的几种常见结构
为了方便表述,我们把一个序列中的数据以时刻(time stamp)来进行划分。简单来讲,我们可以认为时刻0对应的就是序列中第一个元素;时刻1对应的是第2个元素,以此类推。如果将之前的递归计算方式用时刻的概念来表述,便能更加容易地对网络进行理解。下面我们采用这种方法来介绍RNN的三种常见结构。
结构一
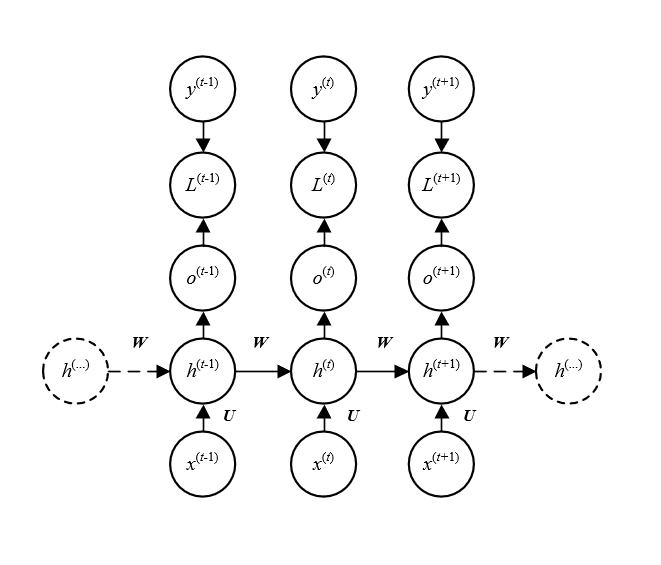
上图所示的RNN结构中,输入序列为
X
=
(
x
0
,
x
1
,
.
.
.
,
x
l
−
1
)
X=(x^{0}, x^{1}, ...,x^{l-1} )
X=(x0,x1,...,xl−1)。对于任意时刻
t
t
t,
h
t
h^t
ht由
h
t
−
1
h^{t-1}
ht−1和
x
t
x^t
xt决定。同时,时刻
t
t
t对应于目标输出(target)
y
t
y^t
yt。这样的结构很适合时间序列预测类的任务,因为模型能够通过之前的信息
h
t
−
1
h^{t-1}
ht−1和当前的输入
x
t
x^t
xt来预测当前时刻的输出
y
^
t
hat y^t
y^t。该结构最大的问题是时刻
t
t
t的损失
L
t
L^{t}
Lt与所有之前时刻的状态
h
t
−
1
,
h
t
−
2
,
.
.
.
,
h
0
h^{t-1}, h^{t-2},... ,h^{0}
ht−1,ht−2,...,h0都相关。这意味着要求得
h
t
h^{t}
ht,首先需要求
h
t
−
1
h^{t-1}
ht−1;而要求
h
t
−
1
h^{t-1}
ht−1,又首先得求出
h
t
−
2
h^{t-2}
ht−2,以此类推。我们知道,在使用BP(Back Propagation,反向传播)求梯度的时候,对每一个输入需要一次前向传播过程来计算网络中的activation。而上述RNN是顺序计算的,难以并行化,因此其训练过程通常比较耗时。
结构二
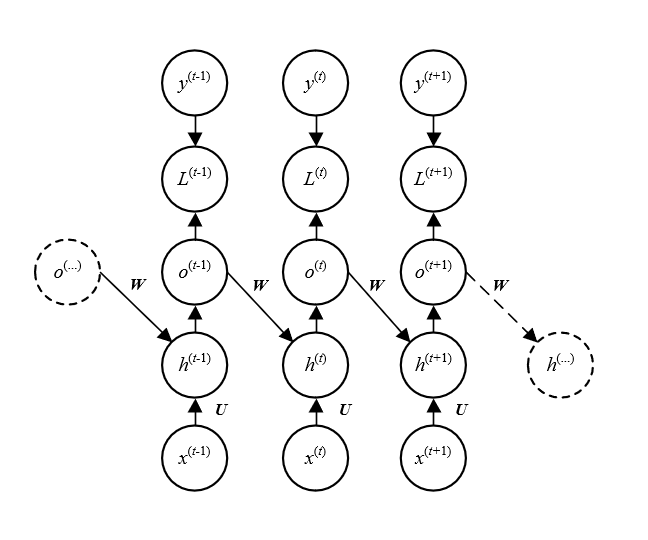
与前文介绍的第一种RNN结构的区别在于:这种结构取消了相邻时刻间状态
h
h
h之间 的连接。取而代之的是前一时刻的输出
o
t
−
1
o^{t-1}
ot−1与当前时刻的状态
h
t
h^t
ht之间的连接。采用与结构一中类似的分析可知,该RNN结构仍是顺序执行的,似乎除了训练参数可能减少(输出
o
{ o}
o的维度通常比
h
h
h要小),没有其它任何区别。不过实际上,这种网络可以采用名为teacher forcing的方法来训练。简单来讲,既然
h
t
h^t
ht的输入部分来自
o
t
−
1
o^{t-1}
ot−1,而
o
t
−
1
o^{t-1}
ot−1本身在训练过程中受
y
t
−
1
y^{t-1}
yt−1约束(
o
t
−
1
o^{t-1}
ot−1要尽可能逼近
y
t
−
1
y^{t-1}
yt−1),因此可以直接使用
y
t
−
1
y^{t-1}
yt−1来代替
o
t
−
1
o^{t-1}
ot−1作为
h
t
h^t
ht的输入。而任意时刻的
y
t
y^{t}
yt在训练集中已经被提供,所以网络在训练过程中不再需要顺序执行!
不过,这样做的缺点就是 y t y^{t} yt中通常包含的信息远少于 h t h^{t} ht,因此模型对历史信息的学习能力远不如结构一。
结构三
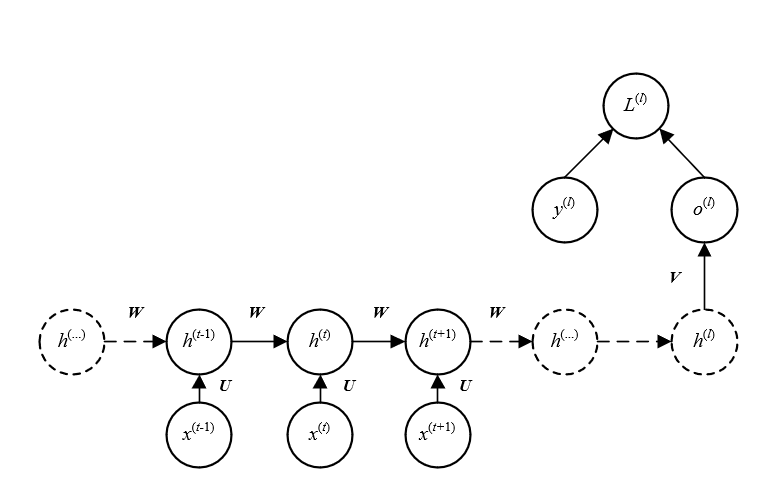
与结构一的唯一区别是:该结构的RNN仅在最后一个时刻
l
l
l时才会有输出
o
l
o^l
ol。显然,这种结构的典型应用就是分本分类。
3. RNN的梯度推导
就求解梯度而言,上述介绍的三种结构的异同如下:
- 在结构一中,当前状态 h t h^t ht不但会影响当前时刻的损失 l t l^t lt,也会影响所有后续时刻的损失;
- 在结构二中,如果采用teacher forcing的训练方法,当前时刻的状态 h t h^t ht只会影响当前时刻的损失 l t l^t lt,并不影响后续时刻的损失;
- 在结构三中,所有时刻的状态均只影响最后的损失(因为只有这一个损失)。
由上述分析可知,结构一的梯度求解是最复杂的。因此,本文仅给出结构一的梯度推导,其它两种结构读者可以自行推导。
我们首先假定输出 y ^ ( t ) hat y^{(t)} y^(t)是一个经softmax得到的概率分布。可以把这样的结构想象成一个词性标注问题,即对于每一个输入的词 x ( t ) x^{(t)} x(t),需要将其标注为“名词”、“动词”、“数量词”等有限的词性集合中的一个。那么,softmax得到的概率分布中的每一个概率对应于一个词性。在此假设下,给出结构一的形式化定义:
(1) h ( t ) = t a n h ( b + W h ( t − 1 ) + U x ( t ) ) , pmb h^{(t)}=mathtt{tanh}(pmb b + pmb W pmb h^{(t-1)} + pmb U pmb x^{(t)}), tag{1} hhh(t)=tanh(bbb+WWWhhh(t−1)+UUUxxx(t)),(1)
(2) y ^ ( t ) = s o f t m a x ( c + V h ( t ) ) . hat y^{(t)}=mathtt{softmax}(pmb c + pmb V pmb h^{(t)}).tag{2} y^(t)=softmax(ccc+VVVhhh(t)).(2)
我们首先来梳理一下上述各矩阵的大小。观察公式(1),假设输入 x ( t ) x^{(t)} x(t)是大小为n的向量(向量均指列向量;即可以看作是大小为(n,1)的矩阵);状态 h ( t ) pmb h^{(t)} hhh(t)和 h ( t − 1 ) pmb h^{(t-1)} hhh(t−1)是大小为k的向量。约定 t a n h mathtt {tanh} tanh作用于矩阵时相当于对矩阵中的每一个元素 x i , j x_{i,j} xi,j分别执行 t a n h ( x i , j ) mathtt {tanh}(x_{i,j}) tanh(xi,j)。
因为矩阵加法和 t a n h mathtt {tanh} tanh函数均不会影响矩阵的大小,故可知公式(1)中的 b pmb b bbb、 W h ( t − 1 ) pmb W pmb h^{(t-1)} WWWhhh(t−1)和 U x ( t ) pmb U pmb x^{(t)} UUUxxx(t)均与 h ( t ) {pmb h^{(t)}} hhh(t)具有相同的大小,即(k, 1)。那么, U pmb U UUU的大小为(k, n), W pmb W WWW的大小为(k, k), b pmb b bbb的大小为(k, 1)。
类似的,公式(2)中的softmax也不会改变它输入矩阵的大小。那么假设 y ^ ( t ) hat y^{(t)} y^(t)的大小为(m, 1),可知 c pmb c ccc的大小为(m, 1), V { pmb V} VVV的大小为(m, n)。为了方便后续推导,将公式(1)和公式(2)进行如下改写:
(3) a ( t ) = b + W h ( t − 1 ) + U x ( t ) , pmb a^{(t)}=pmb b + pmb W pmb h^{(t-1)} + pmb U pmb x^{(t)}, tag{3} aaa(t)=bbb+WWWhhh(t−1)+UUUxxx(t),(3)
(4) h ( t ) = t a n h ( a ( t ) ) , pmb h^{(t)}=mathtt{tanh}(pmb a^{(t)}), tag{4} hhh(t)=tanh(aaa(t)),(4)
(5) o ( t ) = c + V h ( t ) , pmb o^{(t)}=pmb c + pmb V pmb h^{(t)}, tag{5} ooo(t)=ccc+VVVhhh(t),(5)
(6)
y
^
(
t
)
=
s
o
f
t
m
a
x
(
o
(
t
)
)
.
hat y^{(t)}=mathtt{softmax}(pmb o^{(t)}). tag{6}
y^(t)=softmax(ooo(t)).(6)
(抱歉公式(2)和(6)中的
y
^
(
t
)
hat y^{(t)}
y^(t)没有用加粗斜体,因为MathJax的渲染真的太难看!!!)
假设单个时刻的损失函数定义为交叉熵(Cross-entropy):
(7)
L
(
t
)
=
l
o
s
s
(
y
^
(
t
)
,
y
(
t
)
)
=
−
∑
i
y
i
(
t
)
l
o
g
(
y
^
i
(
t
)
)
,
L^{(t)}=loss(hat y^{(t)}, y^{(t)})=-sum_{i}y^{(t)}_i log (hat y^{(t)}_i), tag{7}
L(t)=loss(y^(t),y(t))=−i∑yi(t)log(y^i(t)),(7)
其中
y
(
t
)
y^{(t)}
y(t)表示真实的标签分布;下标
i
i
i表示对应向量的第
i
i
i个分量。那么总体损失即为:
(8)
L
=
∑
t
=
0
l
−
1
L
(
t
)
,
L= sum_{t=0}^{l-1}L^{(t)}, tag{8}
L=t=0∑l−1L(t),(8)
其中 l l l为序列长度。
我们需要求解的梯度为 ∇ c L nabla_c L ∇cL、 ∇ b L nabla_b L ∇bL、 ∇ U L nabla_U L ∇UL、 ∇ V L nabla_V L ∇VL和 ∇ W L nabla_W L ∇WL (因为渲染问题,下标未使用加粗斜体)。
我们首先求解
∇
V
L
nabla_V L
∇VL。由链式法则可知:
(9)
∇
V
L
=
∑
t
=
0
l
−
1
∂
L
∂
L
(
t
)
∂
L
(
t
)
∂
y
^
(
t
)
∂
y
^
(
t
)
∂
o
(
t
)
∂
o
(
t
)
∂
V
.
nabla_V L= sum_{t=0}^{l-1} frac{partial L}{partial L^{(t)}} frac{partial L^{(t)}}{partial hat y^{(t)}} frac{partial hat y^{(t)}}{partial pmb o^{(t)}} frac{partial pmb o^{(t)}}{partial pmb V}. tag{9}
∇VL=t=0∑l−1∂L(t)∂L∂y^(t)∂L(t)∂ooo(t)∂y^(t)∂VVV∂ooo(t).(9)
由公式(8)可得:
(10)
∂
L
∂
L
(
t
)
=
1.
frac{partial L}{partial L^{(t)}}=1. tag{10}
∂L(t)∂L=1.(10)
接着考察第二项
∂
L
(
t
)
∂
y
^
(
t
)
frac{partial L^{(t)}}{partial hat y^{(t)}}
∂y^(t)∂L(t):
(11)
(
∂
L
(
t
)
∂
y
^
(
t
)
)
i
=
(
∇
y
^
(
t
)
L
(
t
)
)
i
=
−
∂
y
i
(
t
)
l
o
g
y
^
i
(
t
)
∂
y
^
i
(
t
)
=
−
y
i
(
t
)
y
^
i
(
t
)
.
(frac{partial L^{(t)}}{partial hat y^{(t)}})_i=(nabla_{hat y^{(t)}}L^{(t)})_i=-frac{partial y_i^{(t)}log hat y_i^{(t)}}{partial hat y_i^{(t)}} = -frac{y_i^{(t)}}{hat y_i^{(t)}}.tag{11}
(∂y^(t)∂L(t))i=(∇y^(t)L(t))i=−∂y^i(t)∂yi(t)logy^i(t)=−y^i(t)yi(t).(11)
再来看第三项
∂
y
^
(
t
)
∂
o
(
t
)
frac{partial hat y^{(t)}}{partial o^{(t)}}
∂o(t)∂y^(t)。由公式(6)知,
(12)
y
^
i
(
t
)
=
e
(
o
i
(
t
)
)
∑
k
e
(
o
k
(
t
)
)
.
hat y^{(t)}_i = frac{e^{(o^{(t)}_i)}}{sum_{k}e^{(o^{(t)}_k)}}.tag{12}
y^i(t)=∑ke(ok(t))e(oi(t)).(12)
注意到在公式(12)中,
o
(
t
)
o^{(t)}
o(t)的每一分量都在分母中出现,而只有一个分量在分子中出现,且该分量的下标
i
i
i对应于所求
y
^
(
t
)
hat y^{(t)}
y^(t)的下标。因此,在求解偏导数
∂
y
^
i
(
t
)
∂
o
j
(
t
)
frac{partial hat y_i^{(t)}}{partial o^{(t)}_j}
∂oj(t)∂y^i(t)时,需要考虑
i
i
i和
j
j
j是否相等。
若
i
i
i与
j
j
j不相等,
(13)
∂
y
^
i
(
t
)
∂
o
j
(
t
)
=
∂
∂
o
j
(
t
)
(
e
(
o
i
(
t
)
)
∑
k
e
(
o
k
(
t
)
)
)
=
−
e
(
o
i
(
t
)
)
e
(
o
j
(
t
)
)
(
∑
k
e
(
o
k
(
t
)
)
)
2
=
−
y
^
i
(
t
)
y
^
j
(
t
)
.
frac{partial hat y_i^{(t)}}{partial o^{(t)}_j}= frac{partial}{partial o^{(t)}_j} (frac{e^{(o^{(t)}_i)}}{sum_{k}e^{(o^{(t)}_k)}})=-frac{e^{(o^{(t)}_i)}e^{(o^{(t)}_j)}}{(sum_{k}e^{(o^{(t)}_k)})^2}=-hat y^{(t)}_i hat y^{(t)}_j.tag{13}
∂oj(t)∂y^i(t)=∂oj(t)∂(∑ke(ok(t))e(oi(t)))=−(∑ke(ok(t)))2e(oi(t))e(oj(t))=−y^i(t)y^j(t).(13)
若
i
i
i与
j
j
j相等(都记为
i
i
i),则有:
(14)
∂
y
^
i
(
t
)
∂
o
i
(
t
)
=
∂
∂
o
i
(
t
)
(
e
(
o
i
(
t
)
)
∑
k
e
(
o
k
(
t
)
)
)
=
−
e
(
o
i
(
t
)
)
∑
k
e
(
o
k
(
t
)
)
−
e
(
o
i
(
t
)
)
e
(
o
i
(
t
)
)
(
∑
k
e
(
o
k
(
t
)
)
)
2
=
e
(
o
i
(
t
)
)
∑
k
e
(
o
k
(
t
)
)
−
(
e
(
o
i
(
t
)
)
∑
k
e
(
o
k
(
t
)
)
)
2
=
y
^
i
(
t
)
(
1
−
y
^
i
(
t
)
)
.
frac{partial hat y_i^{(t)}}{partial o^{(t)}_i}= frac{partial}{partial o^{(t)}_i} (frac{e^{(o^{(t)}_i)}}{sum_{k}e^{(o^{(t)}_k)}})=-frac{e^{(o^{(t)}_i)}sum_{k}e^{(o^{(t)}_k)}-e^{(o_i^{(t)})}e^{(o_i^{(t)})}}{(sum_{k}e^{(o^{(t)}_k)})^2}=frac{e^{(o_i^{(t)})}}{sum_{k}e^{(o^{(t)}_k)}} - (frac{e^{(o_i^{(t)})}}{sum_{k}e^{(o^{(t)}_k)}})^2\ =hat y_i^{(t)}(1-hat y_i^{(t)}).tag{14}
∂oi(t)∂y^i(t)=∂oi(t)∂(∑ke(ok(t))e(oi(t)))=−(∑ke(ok(t)))2e(oi(t))∑ke(ok(t))−e(oi(t))e(oi(t))=∑ke(ok(t))e(oi(t))−(∑ke(ok(t))e(oi(t)))2=y^i(t)(1−y^i(t)).(14)
根据上述推导,我们来梳理一下
∂
L
(
t
)
∂
y
^
(
t
)
∂
y
^
(
t
)
∂
o
(
t
)
frac{partial L^{(t)}}{partial hat y^{(t)}} frac{partial hat y^{(t)}}{partial o^{(t)}}
∂y^(t)∂L(t)∂o(t)∂y^(t)的结果究竟是什么。因为
L
(
t
)
L^{(t)}
L(t) 是标量,
y
^
(
t
)
hat y^{(t)}
y^(t)是大小为m的向量,因此
∂
L
(
t
)
∂
y
^
(
t
)
frac{partial L^{(t)}}{partial hat y^{(t)}}
∂y^(t)∂L(t)同样是一个大小为m的向量(记该向量为
M
pmb M
MMM),该向量第
i
i
i个元素的值是
−
y
i
(
t
)
y
^
i
(
t
)
-frac{y_i^{(t)}}{hat y_i^{(t)}}
−y^i(t)yi(t)(参见公式(11))。因为
y
^
(
t
)
hat y^{(t)}
y^(t)是大小为m的向量,
o
(
t
)
o^{(t)}
o(t)也是大小为m的向量,所以
∂
y
^
(
t
)
∂
o
(
t
)
frac{partial hat y^{(t)}}{partial o^{(t)}}
∂o(t)∂y^(t)的结果是大小为(m, m)的矩阵(记该矩阵为
N
pmb N
NNN)。矩阵的第
i
i
i列为
∂
y
^
(
t
)
∂
o
i
(
t
)
frac{partial hat y^{(t)}}{partial o^{(t) }_i}
∂oi(t)∂y^(t)。那么
(
M
T
×
N
)
T
(M^T times N)^T
(MT×N)T为大小为m的向量,向量的每一个值为
∂
L
(
t
)
∂
o
i
(
t
)
frac{partial L^{(t)}}{partial o^{(t)}_i}
∂oi(t)∂L(t),且这个值的大小为:
(15)
∑
j
,
i
≠
j
(
y
j
(
t
)
y
^
i
(
t
)
)
−
y
i
(
t
)
(
1
−
y
^
i
(
t
)
)
=
−
y
i
(
t
)
+
y
^
i
(
t
)
∑
j
y
j
(
t
)
.
sum_{j,i neq j}(y_j^{(t)}hat y_i^{(t)}) - y_i^{(t)}(1-hat y_i^{(t)})=-y_i^{(t)}+hat y_i^{(t)}sum_j y_j^{(t)}.tag{15}
j,i̸=j∑(yj(t)y^i(t))−yi(t)(1−y^i(t))=−yi(t)+y^i(t)j∑yj(t).(15)
这里需要注意两点。首先, ∂ y ^ ( t ) ∂ o ( t ) frac{partial hat y^{(t)}}{partial o^{(t)}} ∂o(t)∂y^(t)是列向量对列向量求导,其计算结果虽然也为矩阵,但是行列的关系没有明确定义,即谁作为行和谁作为列不明确。因此通常需要结合实际情况来确定计算规则。上述的 ( M T × N ) T (M^T times N)^T (MT×N)T就是为了保证计算的实际意义来设立的计算规则。它将 ∂ L ( t ) ∂ y ^ ( t ) frac{partial L^{(t)}}{partial hat y^{(t)}} ∂y^(t)∂L(t)和 ∂ y ^ ( t ) ∂ o ( t ) frac{partial hat y^{(t)}}{partial o^{(t)}} ∂o(t)∂y^(t)的计算结构进行合并成 ∂ L ( t ) ∂ o ( t ) frac{partial L^{(t)}}{partial o^{(t)}} ∂o(t)∂L(t)的结果。其次,在做推导时,请特别注意 i i i和 j j j在不同公式中对应的对象的差别。例如,在公式(11)中, i i i对应的是 y ^ ( t ) hat y^{(t)} y^(t),而在公式(15)中, i i i对应的是 o ( t ) o^{(t)} o(t)。
通常,
y
(
t
)
y^{(t)}
y(t)中仅有一个分量为1,表示真实类别,而其它分量都为0。因此,
(16)
∑
j
y
j
(
t
)
=
1.
sum_j y_j^{(t)}=1.tag{16}
j∑yj(t)=1.(16)
公式(15)就简化为:
(17)
−
y
i
(
t
)
+
y
^
i
(
t
)
.
-y_i^{(t)}+hat y_i^{(t)}.tag{17}
−yi(t)+y^i(t).(17)
至此,我们把公式(9)中求和符号内的前三项的结果记为:
(18)
∂
L
∂
L
(
t
)
∂
L
(
t
)
∂
y
^
(
t
)
∂
y
^
(
t
)
∂
o
(
t
)
=
∇
o
(
t
)
L
,
frac{partial L}{partial L^{(t)}} frac{partial L^{(t)}}{partial hat y^{(t)}} frac{partial hat y^{(t)}}{partial pmb o^{(t)}}=nabla_{o^{(t)}}L,tag {18}
∂L(t)∂L∂y^(t)∂L(t)∂ooo(t)∂y^(t)=∇o(t)L,(18)
该列向量的第
i
i
i个分量的值为
−
y
i
(
t
)
+
y
^
i
(
t
)
-y_i^{(t)}+hat y_i^{(t)}
−yi(t)+y^i(t)。
最后考察公式(9)中求和符号内的最后一项
∂
o
(
t
)
∂
V
frac{partial o^{(t)}}{partial V}
∂V∂o(t)。由公式(5)和矩阵求导公式可知:
(19)
∂
o
(
t
)
∂
V
=
(
h
(
t
)
)
T
.
frac{partial pmb o^{(t)}}{partial pmb V}=(h^{(t)})^{T}.tag{19}
∂VVV∂ooo(t)=(h(t))T.(19)
因此,我们要求的第一个梯度
∇
V
L
nabla_V L
∇VL的结果为:
(20)
∇
V
L
=
∑
t
=
0
l
−
1
∇
o
(
t
)
L
(
h
(
t
)
)
T
.
nabla_V L=sum_{t=0}^{l-1} nabla_{o^{(t)}}L(h^{(t)})^T.tag{20}
∇VL=t=0∑l−1∇o(t)L(h(t))T.(20)
(先到这,空了继续码)
最后
以上就是精明小蚂蚁最近收集整理的关于RNN介绍及梯度详细推导1. RNN简介2. RNN的几种常见结构3. RNN的梯度推导的全部内容,更多相关RNN介绍及梯度详细推导1.内容请搜索靠谱客的其他文章。








发表评论 取消回复