内容

• Legendre 多项式
  • Legendre 多项式的完备正交归一性
  • 对 Legendre 级数展开
  • Legendre 多项式的生成函数
• 连带 Legendre 多项式
• 球谐函数

---

正交曲面坐标系下的 Helmholtz 方程

$$({\nabla }^2+k^2)u=0$$

Legendre 多项式

引入

在球坐标系中对 Helmholtz 方程 $({\nabla }^2+k^2)u(r,\theta ,\phi )=0$ 分离变量，得到

$$u(r,\theta ,\phi )=R(r)\Theta (\theta )\Phi (\phi )\Rightarrow \{\begin{array}{l}\frac{1}{r^2}\frac{\mathrm{d}}{\mathrm{d}r}\left(r^2\frac{\mathrm{d}R(r)}{\mathrm{d}r}\right)+\left(k^2-\frac{\lambda }{r^2}\right)R(r)=0\\ \frac{1}{\sin \theta }\frac{\mathrm{d}}{\mathrm{d}\theta }\left(\sin \theta \frac{\mathrm{d}\Theta (\theta )}{\mathrm{d}\theta }\right)+\left(\lambda -\frac{\mu }{{\sin }^2\theta }\right)\Theta (\theta )=0\\ \frac{{\mathrm{d}}^2\Phi (\phi )}{\mathrm{d}{\phi }^2}+\mu \Phi (\phi )=0\end{array}$$
其中 $\lambda ,\mu$ 是在分离变量过程中产生的参数。
对 $\Theta (\theta )$ 的方程作换元 $x=\cos \theta$ ，从而 $y(x)=\Theta (\theta )$ ， $\frac{\mathrm{d}}{\mathrm{d}x}=-\frac{1}{\sin \theta }\frac{\mathrm{d}}{\mathrm{d}\theta }$ 。方程变为

$$\frac{\mathrm{d}}{\mathrm{d}x}\left[(1-x^2)\frac{\mathrm{d}}{\mathrm{d}x}y(x)\right]+\left[\lambda -\frac{\mu }{1-x^2}\right]y=0$$
称为 连带 Legendre 方程 。如果 $\mu =0$ 就简化为 Legendre 方程 。
首先讨论 Legendre 方程。为了求解，先研究方程和解 $w(z)$ 在复数域上的性质。

$$\frac{\mathrm{d}}{\mathrm{d}z}\left[(1-z^2)\frac{\mathrm{d}}{\mathrm{d}z}w\right]+\lambda w=0,\lambda =l(l+1)$$
方程有 正则奇点 $\pm 1$ 和 $\infty$ 。

Legendre 方程的级数解

根据以上奇点分析知道，方程的解在 $|z|=1$ 内部解析，可以在 $z=0$ 展成 Taylor 级数。存在两个线性无关的解

$$\begin{array}{rl}w(z)& =c_0{w}_1(z)+c_1{w}_2(z)\\ w_1(z)& =\sum _{n=0}^{\infty }\frac{2^{2n}}{(2n)!}\frac{\Gamma \left(n-\frac{l}{2}\right)}{\Gamma \left(-\frac{l}{2}\right)}\frac{\Gamma \left(n+\frac{l+1}{2}\right)}{\Gamma \left(\frac{l+1}{2}\right)}{z}^{2n}\\ w_2(z)& =\sum _{n=0}^{\infty }\frac{2^{2n}}{(2n+1)!}\frac{\Gamma \left(n-\frac{l-1}{2}\right)}{\Gamma \left(-\frac{l-1}{2}\right)}\frac{\Gamma \left(n+\frac{l}{2}+1\right)}{\Gamma \left(\frac{l}{2}+1\right)}{z}^{2n+1}\end{array}$$
可以估计 $z\to \pm 1$ 时（详见吴崇试. 数学物理方法-第三版, pp. 250 ~ 251）

$$\begin{array}{rl}{w}_1(z)& \sim O\left(\sum _{n=1}^{\infty }\frac{z^{2n}}{n}\right)\sim O\left(\ln \frac{1}{1-z^2}\right)\\ w_2(z)& \sim O\left(\sum _{n=1}^{\infty }\frac{z^{2n+1}}{2n+1}\right)\sim O\left(\ln \frac{1+z}{1-z}\right)\end{array}$$
它们都 在 $\pm 1$ 对数发散 。
进一步知道 $z=\pm 1$ 还是 $w_{1,2}(z)$ 的枝点。对 $w_{1,2}(z)$ 向全平面的解析延拓必然导致多值性。

$z=\pm 1$ 是方程的正则奇点。可以在 $0<|z-1|<2$ 环域作 Laurent 展开 求级数解，结果是：

$$\begin{array}{rl}{P}_l(z)& =\sum _{n=0}^{\infty }\frac{1}{(n!{)}^2}\frac{\Gamma (l+n+1)}{\Gamma (l-n+1)}{\left(\frac{z-1}{2}\right)}^n\\ Q_l(z)& =\frac{1}{2}{P}_l(z)\left[\ln \frac{z+1}{z-1}-2\gamma -2\psi (l+1)\right]+\sum _{n=0}^{\infty }\frac{1}{(n!{)}^2}\frac{\Gamma (l+n+1)}{\Gamma (l-n+1)}\left(1+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}\right){\left(\frac{z-1}{2}\right)}^n\end{array}$$
其中 $P_l(z)$ 称为 $l$ 阶第一类 Legendre 函数 。第二类 Legendre 函数 $Q_l(z)$ 是多值函数，其中 $\psi (z)=(\ln \Gamma (z){)}^{\prime }$ ， $\gamma$ 是欧拉常数。
也可以类似地求出 Legendre 方程在 $z=-1$ 、 $z=\infty$ 邻域内的级数解。

发散问题和解决

回到实际的物理问题。虽然 Legendre 函数是在 Helmholtz 方程本征问题角向问题中导出的，对于 Laplace 方程本征问题，分离变量后 $\Theta (\theta )$ 也满足相同的常微分方程。

Laplace 算子 ${\nabla }^2$ 在球坐标系下在 $\theta =0,\pi$ 和 $r=0$ 处都没有定义，这是 $(r,\theta ,\phi )$ 定义域的规定导致的。需要添加有界性条件：
$y(\pm 1)$ 表示球的南北两极，在物理上没有特殊性。应当要求 $y(\pm 1)=\Theta (0)or\Theta (\pi )$ 有界。

但根据前面的结果，两个解在 $\pm 1$ 一般是对数发散的。考虑这样的可能，即 $w_{1,2}(z)$ 分别发散，但是某些特殊的参数 $l$ 可以使 $w=c_0{w}_1+c_1{w}_2$ 在 $\pm 1$ 发散性抵消而有界。

更直接的是考察 $w(z)=c_1{P}_l(z)+c_2{Q}_l(z)=c{P}_l(z)$ 。在 $z=1$ 收敛首先要求 $c_2=0$ 。
此时 $w(z)\sim P_l$ ，注意到 $P_l(1)=1$ 。然而不幸地，对于一般 $l$ 值，只要 $P_l(z)$ 还是无穷级数，$P_l(-1)$ 就对数发散。如何才能符合物理实际？

其实，若令 级数 $P_l(z)$ 截断为多项式，即在某一项之后为零 ，即可解决 $P_l(-1)$ 处的有界性。
亦即 求 $l$ 使得 $\forall n\in \mathbb{N}$ ：

$$\frac{\Gamma (l+n+1)}{\Gamma (l-n+1)}=\frac{\cdots }{\infty }=0\Rightarrow \{\begin{array}{ll}l+n+1>0,& \forall n\ge 0,\\ l-n+1=0,-1,\cdots & \exists N\in {\mathbb{Z}}^{+},\forall n>N\end{array}$$
推出 $l$ 为自然数，即 $l\in \mathbb{N}$ 。此时

$$P_l(z)=\sum _{n=0}^{\infty }\frac{1}{(n!{)}^2}\frac{(l+n{)}^2}{(l-n{)}^2}{\left(\frac{z-1}{2}\right)}^n=\sum _{n=0}^l\frac{1}{(n!{)}^2}\frac{(l+n{)}^2}{(l-n{)}^2}{\left(\frac{z-1}{2}\right)}^n$$
$P_l(x)$ 是一个 $l$ 次多项式，称为 $l$ 阶 Legendre 多项式 。

$$\begin{array}{rlrl}{P}_0(x)& =1& P_1(x)& =x\\ P_2(x)& =\frac{3}{2}{x}^2-\frac{1}{2}& P_3(x)& =\frac{5}{2}{x}^3-\frac{3}{2}x\\ \cdots & & & \end{array}$$
利用 $x=1$ 处的展开表示，还可以得到

$$P_l(1)=\frac{1}{(0!{)}^2}\frac{(l+0{)}^2}{(l-0{)}^2}=1$$

Legendre 多项式的微分表示（aka. Rodrigues 公式）

$$P_l(x)=\frac{1}{2^{l}l!}\frac{{\mathrm{d}}^l}{\mathrm{d}{x}^l}\left[(x^2-1{)}^l\right]$$
证明只需要直接（Brute Force）计算

$$\begin{array}{rl}(x^2-1{)}^l& =(x-1{)}^l(x-1+2{)}^l\\ & =\sum _{n=0}^l\left(\begin{array}{c}l\\ n\end{array}\right)2^{l-n}(x-1{)}^{l+n}\\ \frac{1}{l!2^l}\frac{{\mathrm{d}}^l}{\mathrm{d}{x}^l}[(x^2-1{)}^l]& =\sum _{n=0}^l\frac{2^{-n}}{n!(l-n)!}\frac{{\mathrm{d}}^l}{\mathrm{d}{x}^l}[(x-1{)}^{l+n}]\\ & =\sum _{n=0}^l\frac{2^{-n}}{n!(l-n)!}\frac{(l+n)!}{n!}(x-1{)}^n\\ & =\sum _{n=0}^l\frac{1}{(n!{)}^2}\frac{(l+n)!}{(l-n)!}{\left(\frac{x-1}{2}\right)}^n\end{array}$$

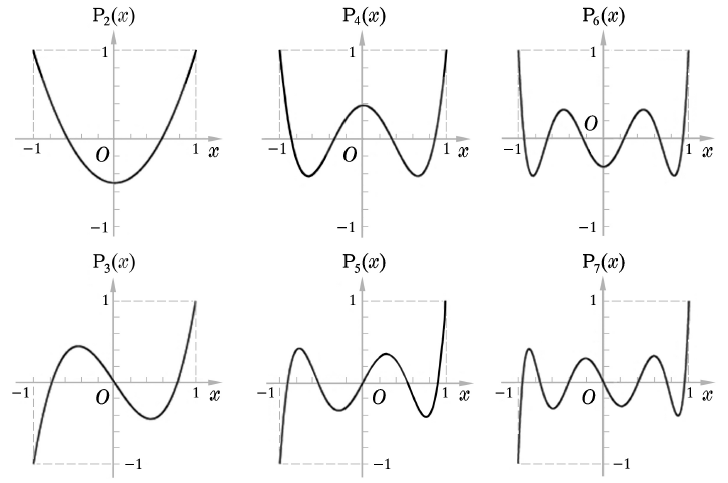
换元知 $P_l(-x)=(-1{)}^l{P}_l(x)$ ，这表明 奇（偶）数阶 Legendre 多项式是奇（偶）宇称 。这也给出

$$P_l(-1)=(-1{)}^l$$
观察 $P_l(x)$ 的无穷级数表示，发现奇数阶多项式的每一个单项都是 $x$ 的奇次幂，偶数阶多项式 vice versa。

可以想见，一旦含有任一个【相反宇称的项】就会破坏整体的宇称。因为再多个其它幂次项都不可能抵消某一不同幂次项的贡献。

以x为宗量的表示

希望得到以 $x$ 为宗量的表示，就如最开始推导那样。
仅需对 Rodrigues 公式中的 $(x^2-1{)}^l$ 作二项展开再求导，得到

$$P_l(x)=\sum _{n=0}^{\lfloor l/2\rfloor }(-1{)}^n\frac{(2l-2n)!}{2^{l}n!(l-n)!(l-2n)!}{x}^{l-2n}$$

Legendre 多项式的标准积分

讨论以下积分

$$I_l^k={\int }_{-1}^{+1}{x}^k{P}_l(x)\mathrm{d}x$$

1. $k+l$ 为奇数时 被积函数有奇宇称 ，在对称区间 $[-1,+1]$ 上积分为零
2. 否则可以设 $k=l+2n,n\in \mathbb{Z}$ 。首先说明 $k<l$ 时， $I_l^k=0$ ：
   利用 Rodrigues 公式，并简记 $\frac{{\mathrm{d}}^l}{\mathrm{d}{x}^l}={\partial }^l$ ，作分部积分：

$$\begin{array}{rl}{I}_l^k& =\frac{1}{2^{l}l!}\int x^k{\partial }^l[(x^2-1{)}^l]\mathrm{d}x\\ & =\frac{1}{2^{l}l!}\left[\right\{x^k{\partial }^{l-1}[(x^2-1{)}^l\left]\right\}{|}_{-1}^{+1}-\int \partial (x^k){\partial }^{l-1}[(x^2-1{)}^l\left]\mathrm{d}x\right]\\ & =-\frac{1}{2^{l}l!}\int \partial (x^k){\partial }^{l-1}[(x^2-1{)}^l]\mathrm{d}x\\ & =\cdots \\ & =\frac{(-1{)}^l}{2^{l}l!}\int {\partial }^l(x^k)(x^2-1{)}^l\mathrm{d}x\end{array}$$

${\partial }^{a-1}(x^k){\partial }^{l-a}[(x^2-1{)}^l]1\le a\le l$ 是偶函数。

${\partial }^l(x^k)\equiv 0\forall l>k$ 。

所以 $l>k$ 时 $I_l^k=0$ 。
对于 $l\ge k$ ，作换元 $l=k+2n,n=0,1,2,\cdots$ ，上述分部积分继续写成

$$\begin{array}{rl}{\int }_{-1}^{+1}{x}^{l+2n}{P}_l(x)\mathrm{d}x& =\frac{(-1{)}^l}{2^{l}l!}{\int }_{-1}^{+1}{\partial }^l(x^{l+2n})(x^2-1{)}^l\mathrm{d}x\\ & =\frac{(-1{)}^l}{2^{l}l!}\frac{(l+2n)!}{(2n)!}{\int }_{-1}^{+1}(x^2{)}^n(x^2-1{)}^l\frac{\mathrm{d}x}{2x}\\ & =\frac{1}{2^{l}l!}\frac{(l+2n)!}{(2n)!}\mathrm{B}\left(n+\frac{1}{2},l+1\right)\\ & =2^{l+1}\frac{(l+2n)!(l+n)!}{n!(2l+2n+1)!}\end{array}$$

$\mathrm{d}x=\frac{\mathrm{d}x}{2x}$ 产生的 $\frac{1}{2}$ 在积分区间折半时抵消（ cancel out ）

Legendre 多项式的完备正交归一性

正交性和归一性都可以通过 Legendre 多项式的标准积分推导。具体地：

正交性

由于 $l<k$ 时 $I_l^k=0$ ，积分

$${\int }_{-1}^{+1}{P}_l(x)P_k(x)\mathrm{d}x\sim \sum _{n=0}^l{\int }_{-1}^{+1}{x}^n{P}_k(x)\mathrm{d}x=\sum _{n=0}^l{I}_l^n=0$$
考虑对称性，就有

$${\int }_{-1}^{+1}{P}_l(x)P_k(x)=0,\forall l\ne k$$

归一性

在 Legendre 多项式的标准积分中令 $k=l$ ，就有

$${\int }_{-1}^{+1}{P}_l(x)P_l(x)\mathrm{d}x=c_l{I}_l^l=\frac{(2l)!}{(l!{)}^2{2}^l}\frac{2^{l+1}(l!{)}^2}{(2l+1)!}=\frac{2}{2l+1}$$

$P_l(x)P_l(x)$ 写成 $P_l^2(x)$ 不合适，会和连带 Legendre 多项式混淆。

于是可以将 Legendre 多项式的正交归一性合写成

$${\int }_{-1}^{+1}{P}_k(x)P_l(x)\mathrm{d}x=\frac{2}{2l+1}{\delta }_{kl}$$
如果回到本来的 $\Theta (\theta )$ 问题，上述结论又写成

$${\int }_0^{\pi }{P}_k(\cos \theta )P_k(\cos \theta )\sin \theta \mathrm{d}\theta =\frac{2}{2l+1}{\delta }_{kl}$$

积分换元和交换积分限各产生一个负号，cancel out。

即不同阶 Legendre 多项式在区间 $[0,\pi ]$ 上以 权函数 $\sin \theta$ 正交 。

完备性

任一个在 $[-1,1]$ 上分段连续的函数 $f(x)$ 在平均收敛的意义上都可以展成 Legendre 级数

$$f(x)\sim \sum _{l=0}^{\infty }{c}_l{P}_l(x)$$
其中平均收敛指

$$\underset{N\to \infty }{\lim }{\int }_{-1}^{+1}{\left|f(x)-\sum _{l=0}^N{c}_l{P}_l(x)\right|}^2\mathrm{d}x=0$$

对 Legendre 级数展开

Legerdre 级数表示

$$f(x)=\sum _{l=0}^{\infty }{c}_l|l⟩=\sum _{l=0}^{\infty }{c}_l{P}_l(x)$$

展开系数

$$c_l=\frac{2l+1}{2}⟨f(x)|l⟩=\frac{2l+1}{2}{\int }_{-1}^{+1}f(x)P_l(x)\mathrm{d}x$$

计算展开系数

对多项式 $f(x)$ 作展开时，首先注意到展开式中不可能有超过 $\mathrm{deg}f(x)-$ 阶 Legendre 多项式。类似长除法，先除以 $P_{\mathrm{deg}f}(x)$ ，余式再除以 $P_{\mathrm{deg}f-2}(x)$ ……
展开的唯一性保证这样得到的一定是正确结果。

Legendre 多项式的生成函数

Legendre 多项式首先是在势论研究中引进的。在球坐标系中，一个 $q=+\frac{1}{4\pi \epsilon }$ 的点电荷位于 $\mathbf{r}=(r,0,\ast )$ 处，则 ${\mathbf{r}}^{\prime }=(r^{\prime },{\theta }^{\prime },{\phi }^{\prime })$ 处的电势为

$\ast$ 代表任意取值，因为该点 $\theta =0$ 在 $z$ 轴上。

$$\frac{1}{|\mathbf{r}-{\mathbf{r}}^{\prime }|}=\frac{1}{\sqrt{r^2+r^{\prime 2}-2r{r}^{\prime }\cos {\theta }^{\prime }}}\stackrel{x=\cos {\theta }^{\prime }}{=}\{\begin{array}{l}\frac{1}{r}\frac{1}{\sqrt{1-2xt+t^2}},t=\frac{r^{\prime }}{r}\\ \frac{1}{r^{\prime }}\frac{1}{\sqrt{1-2xt+t^2}},t=\frac{r}{r^{\prime }}\end{array}$$

注意到 $f(t)=\frac{1}{\sqrt{1-2xt+t^2}}$ 有多值性。其枝点 $t_{1,2}=x\pm \sqrt{x^2-1}$ ，作连接两枝点的割线，并规定单值分支

$$\frac{1}{\sqrt{1-2xt+t^2}}{|}_{t=0}=1$$
这样只要作的割线不通过 $t=0$ ，函数就在 $t=0$ 的领域中解析，从而可以 Taylor 展开。下面说明展开系数就是各阶 Legendre 多项式，即

1 1 − 2 x t + t 2 = ∑ l = 0 ∞ P l ( x ) t l , ∣ t ∣ < min ⁡ { x ± x 2 − 1 } frac{1}{sqrt{1-2xt+t^2}}=sum_{l=0}^{infty}P_l(x)t^l,qquad|t|<min{xpmsqrt{x^2-1}} 1−2xt+t2 ​1​=l=0∑∞​Pl​(x)tl,∣t∣<min{x±x2−1 ​}
仅需在 $t=0$ 圆域内作 Taylor 级数展开

$$\begin{array}{rl}\frac{1}{\sqrt{1-2xt+t^2}}& =\frac{1}{\sqrt{(1-t{)}^2-2(x-1)t}}\\ & =\frac{1}{1-t}{\left[1-\frac{2(x-1)t}{(1-t{)}^2}\right]}^{-1/2}\\ & =\frac{1}{1-t}\sum _{k=0}^{+\infty }\frac{1}{k!}\left(-\frac{1}{2}\right)\left(-\frac{3}{2}\right)\cdots \left(\frac{1}{2}-k\right){\left[1-\frac{2(x-1)t}{(1-t{)}^2}\right]}^k\\ & =\sum _{k=0}^{+\infty }\frac{(2k-1)!!}{k!}(x-1{)}^k{t}^k(1-t{)}^{-(2k+1)}\\ & =\sum _{k=0}^{+\infty }\frac{(2k-1)!!}{k!}(x-1{)}^k{t}^k\sum _{n=0}^{+\infty }\frac{(2k+n)!}{(2k)!n!}{t}^n\\ & \stackrel{l=k+n}{=}\sum _{l=0}^{+\infty }\left[\sum _{k=0}^l\frac{(l+k)!}{k!k!(l-k)!}{\left(\frac{x-1}{2}\right)}^k\right]t^l\\ & =\sum _{l=0}^{+\infty }{P}_l(x)t^l\end{array}$$

$(1-t{)}^{-(2k+1)}$ 的展开用到

$$\frac{1}{(1-t{)}^s}=\sum _{k=0}^{+\infty }\left(\begin{array}{c}s+k-1\\ k\end{array}\right)x^k$$

注意到两个枝点 $t_1{t}_2=1$ ，所以上述级数的收敛域不超过单位圆。
称 $\frac{1}{\sqrt{1-2xt+t^2}}$ 为 $P_l(x)$ 的 生成函数 。

利用生成函数可以【参见吴崇试. 数理方法-第三版, pp. 260-261】

• 计算 Legendre 多项式在一些特殊点的取值
• 推导 Legendre 多项式的宇称
• 讨论 Legendre 多项式的正交性和归一性
• 计算奇形怪状的积分

更重要的是以下若干独特的应用。

相邻阶 Legendre 多项式的递推关系

已经知道

$$\frac{1}{\sqrt{1-2xt+t^2}}=\sum _{l=0}^{\infty }{P}_l(x)t^l$$
上式分别对 $x,t$ 求导并整理，就得到

$$\begin{array}{rlr}{P}_l(x)& =P_{l+1}^{\prime }(x)-2x{P}_l^{\prime }(x)+P_{l-1}^{\prime }(x)& (1)\\ (2l+1)x{P}_l(x)& =(l+1)P_{l+1}(x)+l{P}_{l-1}(x)& (2)\end{array}$$
将 $(2)$ 对 $x$ 求导并和 $(1)$ 联立，还可以得到

$$\begin{array}{rl}{P}_{l+1}^{\prime }(x)& =x{P}_l^{\prime }(x)+(l+1)P_l(x)\\ P_{l-1}^{\prime }(x)& =x{P}_l^{\prime }(x)-l{P}_l(x)\end{array}$$
这可以用于计算一些积分，例如

$${\int }_{-1}^{1}x{P}_k(x)P_l(x)\mathrm{d}x$$
就可以利用 $(2)$ 式，把 $x$ 项吸收而变为两个 $P_k{P}_l$ 类型的积分，利用正交归一性计算。

连带 Legendre 函数

回顾

指标方程和正则解

常系数二阶常微分方程 $w^{\prime \prime }+p(z)w^{\prime }+q(z)w=0$ ，设 $z_0\ne \infty$ 是 $p(z)$ 或 $q(z)$ 的奇点，且满足 $(z-z_0)p(z)$ 和 $(z-z_0{)}^{2}q(z)$ 都在 $z_0$ 处解析，从而 $z_0$ 是方程的正则奇点。
此时方程有 正则解

$$\begin{array}{rl}{w}_1(z)& =(z-z_0{)}^{{\rho }_1}\sum _{k=0}^{+\infty }{c}_k(z-z_0{)}^k\\ w_2(z)& =g{w}_1(z)\ln (z-z_0)+(z-z_0{)}^{{\rho }_2}\sum _{k=0}^{+\infty }{d}_k(z-z_0{)}^k\end{array}$$

用暗红色强调，正则解是 Taylor 性的级数解。

其中 ${\rho }_1,{\rho }_2$ 是方程的 指标 ，满足 指标方程 :

$$\begin{array}{r}\rho (\rho -1)+a_0\rho +b_0=0\\ \{\begin{array}{l}{a}_0=\underset{z\to z_0}{\lim }(z-z_0)p(z)\\ b_0=\underset{z\to z_0}{\lim }(z-z_0{)}^{2}q(z)\end{array}\end{array}$$

连带 Legendre 方程的求解

$$\frac{\mathrm{d}}{\mathrm{d}z}\left[(1-z^2)\frac{\mathrm{d}w(z)}{\mathrm{d}z}\right]+\left(\lambda -\frac{m^2}{1-z^2}\right)w(z)=0,m=0,\pm 1,\pm 2,\cdots$$
它也有正则奇点 $\pm 1,\infty$ 。在 $\pm 1$ 处指标方程的解为 ${\rho }_{1,2}=\pm |m|/2$ ，于是设

$$w(z)=(z^2-1{)}^{|m|/2}v(z)$$

这样的 $w(z)$ 是 $\pm 1$ 邻域中的级数解。

将 $v(z)$ 代入方程，就得到 超球微分方程 ，它在 $m=0$ 时即给出 Legendre 函数 $P_l(z),Q_l(z)$ 。

$$(1-z^2)v^{\prime \prime }(z)-(2|m|+1)z{v}^{\prime }(z)+[\lambda -|m|(|m|+1)]v(z)=0$$

$v(z)$ 在 $\pm 1$ 的指标为 $0,-|m|$ ，显然 $-|m|$ 会导致解发散。上述方程可以用标准级数法求解，但存在另一种更简明的求解方法。

对比 Legendre 方程满足的微分方程 $\frac{\mathrm{d}}{\mathrm{d}z}\left[(1-z^2)\frac{\mathrm{d}w}{\mathrm{d}z}\right]+\lambda w=0$ ，该方程对 $z$ 求导 $|m|$ 次

$$\begin{array}{rlr}(1-z^2)v^{\prime \prime }-2(0+1)z{v}^{\prime }+[\lambda -0(0+1)]v& =0& \text{（Legendre方程）}\\ (1-z^2)v^{\prime \prime \prime }-2(1+1)z{v}^{\prime \prime }+[\lambda -1(1+1)]v^{\prime }& =0& \text{（一阶导）}\\ (1-z^2)v^{\prime \prime \prime \prime }-2(2+1)z{v}^{\prime \prime \prime }+[\lambda -2(2+1)]v^{\prime \prime }& =0& \text{（二阶导）}\\ \cdots & & \end{array}$$
设 Legendre 方程的两个解为 $P_{\nu }(z),Q_{\nu }(z)as\lambda =\nu (\nu +1)$ ，上面的现象表明连带 Legendre 方程的两个线性无关解就是

$$\begin{array}{rl}{P}_{\nu }^{|m|}(z)& =(z^2-1{)}^{|m|/2}\frac{{\mathrm{d}}^{|m|}}{\mathrm{d}{z}^{|m|}}{P}_{\nu }(z)\\ Q_{\nu }^{|m|}(z)& =(z^2-1{)}^{|m|/2}\frac{{\mathrm{d}}^{|m|}}{\mathrm{d}{z}^{|m|}}{Q}_{\nu }(z)\end{array}$$
但以上形式的连带 Legendre 函数并不适合表示 $x\in [-1,1]\subset \mathbb{R}$ 的解 $y(x)$ 【详见吴崇试. 数理方法-第三版, pp. 267】。为此定义

$$\begin{array}{rl}{P}_{\nu }^m(x)& =(-1{)}^{|m|}(1-x^2{)}^{|m|/2}\frac{{\mathrm{d}}^{|m|}}{\mathrm{d}{x}^{|m|}}{P}_{\nu }(x)\\ Q_{\nu }^m(x)& =(-1{)}^{|m|}(1-x^2{)}^{|m|/2}\frac{{\mathrm{d}}^{|m|}}{\mathrm{d}{x}^{|m|}}{Q}_{\nu }(x)\end{array}$$
这样将连带 Legendre 方程的通解写为

$$y(x)=c_1{P}_{\nu }^m(x)+c_2{Q}_{\nu }^m(z)$$

如果要求解的本征值问题是 $y(x)$ 满足连带 Legendre 方程且 $y(\pm 1)$ 有界，就需要讨论 $P_{\nu }^m(x),Q_{\nu }^m(x)$ 在 $x\to \pm 1$ 的行为。

注意区分特征值上标 $P_{\nu }^{|m|}(z)$ 和高阶导数记号 $P_{\nu }^{(|m|)}(x)$

• $P_{\nu }^{|m|}(x)=(1-x^2{)}^{|m|/2}{P}_{\nu }^{(|m|)}(x)$ 在 $1$ 处有界，它就是 $x=1$ 邻域中指标 $|m|/2$ 的解；
• $Q_{\nu }^{|m|}(x)=(1-x^2{)}^{|m|/2}{Q}_{\nu }^{(|m|)}(x)$ 在 $1$ 处发散，它就是 $x=1$ 邻域中指标 $-|m|/2$ 的解。

所以 $y(1)$ 有界要求 $c_2=0$ 。再考虑 $x=-1$ 。只要 $P_{\nu }(x)$ 是无穷级数就在 $x=-1$ 对数发散，从而 $P_{\nu }(x)$ 需要截断为多项式。
同时 $P_{\nu }^{|m|}(x)$ 应当非平凡，利用 Rodrigues 公式

$$P_{\nu }^{|m|}(x)=\frac{(-1{)}^{|m|}}{2^{\nu }\nu !}(1-x^2{)}^{|m|/2}\frac{{\mathrm{d}}^{|m|+\nu }}{\mathrm{d}{x}^{|m|+\nu }}[(x^2-1{)}^{\nu }]$$
故 截断条件为 $|m|\le \nu$ 。吸收符号，在仅相差一个常数倍的意义下连带 Legendre 方程的解为

$$y(x)=\frac{1}{2^{l}l!}(1-x^2{)}^{|m|/2}\frac{{\mathrm{d}}^{|m|+l}}{\mathrm{d}{x}^{|m|+l}}[(x^2-1{)}^l]$$

由于 Legendre 方程对于 $m=\pm |m|$ 形式不变，上述的 $y(x)$ 适用于 $m=\pm |m|$ 两种情况。
特别地将 $m\ge 0$ 的 $y(x)=P_l^m(x)$ 称为 连带 Legendre 多项式 。

定义 $m<0$ 时的 $P_l^m(x)$ 仍然适合

$$\begin{array}{rl}{P}_l^m(x)& =(-1{)}^m\frac{1}{2^{l}l!}(1-x^2{)}^{m/2}\frac{{\mathrm{d}}^{m+l}}{\mathrm{d}{x}^{m+l}}[(x^2-1{)}^l]\\ & =(-1{)}^{|m|}\frac{1}{2^{l}l!}(1-x^2{)}^{-|m|/2}\frac{{\mathrm{d}}^{l-|m|}}{\mathrm{d}{x}^{l-|m|}}[(x^2-1{)}^l]\end{array}$$
这样 $P_l^m(x)=P_l^{-|m|}(x)$ 就和 $P_l^{|m|}(x)$ 线性相关：

$$P_l^{-m}(x)=(-1{)}^m\frac{(l-m)!}{(l+m)!}{P}_l^m(x),m=0,\pm 1,\pm 2,\cdots ,\pm l$$
从而 $\pm m$ 的连带 Legendre 多项式只需要二选一以线性表出方程的解。

正交归一性

相同阶但不同次的连带 Legendre 多项式在区间 $[-1,1]$ 上正交。

$${\int }_{-1}^{+1}{P}_l^m(x)P_k^m(x)\mathrm{d}x=\frac{(l+m)!}{(l-m)!}\frac{2}{2l+1}{\delta }_{kl}$$

球谐函数

Laplace 方程边值问题在球坐标系中求解的结果可以用 球谐函数 表达。为此定义算符

$$\begin{array}{rl}{\hat{l}}_z& =\frac{1}{i}\frac{\partial }{\partial \phi }\\ {\hat{\mathbf{l}}}^2& =-\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial }{\partial \theta }\right)-\frac{1}{\sin \theta }\frac{\partial }{\partial \phi }\left(\frac{1}{\sin \theta }\frac{\partial }{\partial \phi }\right)\end{array}$$

如果角动量的单位取为 $\hslash$ ，上面两个算符在量子力学中有确定的物理含义。

注意到 ${\nabla }^2=\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial }{\partial r}\right)-\frac{{\hat{\mathbf{l}}}^2}{r^2}$ 。

球谐函数 $Y_{lm}(\theta ,\phi )$ 就是 ${\hat{\mathbf{l}}}^2,{\hat{l}}_z$ 的共同本征函数：

$$\begin{array}{rl}{\hat{\mathbf{l}}}^2{Y}_{lm}(\theta ,\phi )& =l(l+1)Y_{lm}(\theta ,\phi )\\ {\hat{l}}_z{Y}_{lm}(\theta ,\phi )& =m{Y}_{lm}(\theta ,\phi )\end{array}$$
满足这样条件的一种球谐函数是

$$\begin{array}{rl}& Y_{lm}(\theta ,\phi )=\sqrt{\frac{2l+1}{4\pi }\frac{(l-|m|)!}{(l+|m|)!}}{P}_l^{|m|}(\cos \theta )e^{im\phi }\\ & l=0,1,2,\cdots \\ & m=0,\pm 1,\pm 2,\cdots ,\pm l\end{array}$$

携带归一化因子

这是一个复函数，但其中可能为复数的项只是 $e^{im\phi }$ 。

球谐函数的以下写法与上式等价：

$$Y_{lm}(\theta ,\phi )=(-1{)}^m\sqrt{\frac{2l+1}{4\pi }\frac{(l-m)!}{(l+m)!}}{P}_l^m(\cos \theta )e^{im\phi }$$

只需注意到 $P_l^{-m}(x)=(-1{)}^m\frac{(l-m)!}{(l+m)!}{P}_l^m(x)$ 。

由于 $(\theta ,\phi )$ 和单位球面上的点 $\mathbf{n}=(\sin \theta \cos \phi ,\sin \theta \sin \phi ,\cos \theta )$ 几乎一一对应，球谐函数的变量也简记作 $\mathbf{n}$ 。
类似地把立体角元记作

$$\frac{\mathrm{d}\tau }{r^2}=\mathrm{d}{\Omega }_{\mathbf{n}}\equiv \mathrm{d}\mathbf{n}\equiv \sin \theta \mathrm{d}\theta \mathrm{d}\phi$$

球谐函数的性质

$$Y_{l(-m)}(\mathbf{n})=(-1{)}^m{Y}_{lm}^{\ast }(\mathbf{n})$$

$(-1{)}^m$ 因子来自归一化的连带 Legendre 多项式，多出的共轭来自 $e^{im\phi }$ 。

正交归一性

$${\int }_{\theta ,\phi }{Y}_{lm}(\mathbf{n})Y_{l^{\prime }{m}^{\prime }}^{\ast }(\mathbf{n})\mathrm{d}\mathbf{n}={\delta }_{m{m}^{\prime }}{\delta }_{l{l}^{\prime }}$$

类似地， ${\delta }_{m{m}^{\prime }}$ 源于 $e^{im\phi }$ 的正交归一性， ${\delta }_{l{l}^{\prime }}$ 源于归一化的连带 Legendre 多项式的正交归一性。

注意到等式右边是一个实函数，取共轭（交换共轭号）不变。

完备性

$$\sum _{l=0}^{+\infty }\sum _{m=-l}^{+l}{Y}_{lm}^{\ast }(\mathbf{n})Y_{lm}({\mathbf{n}}^{\prime })=\delta (\cos {\theta }^{\prime }-\cos \theta )\delta ({\phi }^{\prime }-\phi )$$

$\delta (\cos \theta -\cos {\theta }^{\prime })=\frac{\delta (\theta -{\theta }^{\prime })}{\sin \theta }$

注意到等式右边是一个实函数，取共轭（左边交换共轭号）不变。

球谐函数的应用

Laplace 方程边值问题的解

例如静电问题的解一般可以综合地写成以下形式：

$$\Phi (r,\mathbf{n})=\sum _{l=0}^{+\infty }\sum _{m=-l}^{+l}\left(A_{lm}{r}^l+\frac{B_{lm}}{r^{l+1}}\right)Y_{lm}(\mathbf{n})$$

如果所考虑的问题具有 $\phi$ 方向的对称性， $\Phi$ 的展开就只涉及 $m=0$ 的球谐函数。这时连带 Legendre 多项式退化为 Legendre 多项式。结果直接写成

$$\Phi (r,\theta )=\sum _{l=0}^{+\infty }\left(A_l{r}^l+\frac{B_l}{r^{l+1}}\right)P_l(\cos \theta )$$
再利用 Legendre 多项式的正交归一性 $⟨l|l^{\prime }⟩=\frac{2{\delta }_{l{l}^{\prime }}}{2l+1}$ 定展开系数。

球谐函数的升降算符

$$\cos \theta Y_{lm}(\theta ,\phi )=\frac{z}{r}{Y}_{lm}=$$

$$e^{i\phi }\sin \theta Y_{lm}=\frac{x+iy}{r}{Y}_{lm}=$$

$$e^{-i\phi }\sin \theta Y_{lm}=\frac{x-iy}{r}{Y}_{lm}=$$

$$\begin{array}{rl}{\hat{l}}_{+}{Y}_{lm}& =\sqrt{(l-m)(l+m+1)}{Y}_{l(m+1)}\\ {\hat{l}}_{-}{Y}_{lm}& =\sqrt{(l+m)(l-m-1)}{Y}_{l(m-1)}\end{array}$$

其中 $\{\begin{array}{l}{\hat{l}}_{+}={\hat{l}}_x+i{\hat{l}}_y\\ {\hat{l}}_{-}={\hat{l}}_x-i{\hat{l}}_y\end{array}$

题外话：这一对升降算符作用到 $Y_{lm}$ 产生的系数有种记法：球谐函数的第二个指标 $m$ 的取值范围为 $-l,-l+1,\cdots ,l-1,l$ ，所以应当有

$$\begin{array}{rlr}& {\hat{l}}_{+}{Y}_{ll}\sim Y_{l(l+1)}=0,& \text{升算符含有}(l-m)\\ & {\hat{l}}_{+}{Y}_{l(-l-1)}={\hat{l}}_{+}0=0,& \text{升算符含有}(l+m+1)\\ & {\hat{l}}_{-}{Y}_{l(-l)}\sim Y_{l(-l-1)}=0,& \text{降算符含有}(l+m)\\ & {\hat{l}}_{-}{Y}_{l(l+1)}={\hat{l}}_{+}0=0,& \text{降算符含有}(l-m-1)\end{array}$$

若干函数的展开

• $e^{ikz}=e^{ikr\cos \theta }$

$$e^{ikr\cos \theta }=\sum _{l=0}^{+\infty }{i}^l{j}_l(kr)P_l(\cos \theta )(Rayleig{h}^{\prime }sExpansion)$$

• $\frac{1}{|\mathbf{r}-{\mathbf{r}}^{\prime }|}$

$$\frac{1}{|\mathbf{r}-{\mathbf{r}}^{\prime }|}=\sum _{l=0}^{+\infty }\sum _{m=-l}^{+l}\frac{4\pi }{2l+1}\frac{r_{<}^l}{r_{>}^{l+1}}{Y}_{lm}^{\ast }({\hat{\mathbf{r}}}^{\prime })Y_{lm}(\hat{\mathbf{r}})$$

• $P_l(\cos \alpha )$

$$P_l(\cos \gamma )=\frac{4\pi }{2l+1}\sum _{m=-l}^{+l}{Y}_{lm}^{\ast }({\mathbf{n}}^{\prime })Y_{lm}(\mathbf{n})$$

也称为球谐函数的加法定理。下面将对这一结论详细说明。

球谐函数的加法定理

$$P_l(\cos \gamma )=\frac{4\pi }{2l+1}\sum _{m=-l}^{+l}{Y}_{lm}^{\ast }({\mathbf{n}}^{\prime })Y_{lm}(\mathbf{n})$$

其中 $\gamma$ 是单位球上两个矢量的夹角：

$$\begin{array}{rl}\mathbf{n}& =(\sin \theta \cos \phi ,\sin \theta \sin \phi ,\cos \theta )\\ {\mathbf{n}}^{\prime }& =(\sin {\theta }^{\prime }\cos {\phi }^{\prime },\sin {\theta }^{\prime }\sin {\phi }^{\prime },\cos {\theta }^{\prime })\\ & \cos \gamma =\mathbf{n}\cdot {\mathbf{n}}^{\prime }\end{array}$$

这一结论称为球谐函数的 加法定理 。

对于两个矢量 $\mathbf{r},{\mathbf{r}}^{\prime }$ ，已经有展开式
$$\frac{1}{|\mathbf{r}-{\mathbf{r}}^{\prime }|}=\sum _{l=0}^{+\infty }\sum _{m=-l}^{+l}\frac{4\pi }{2l+1}\frac{r_{<}^l}{r_{>}^{l+1}}{Y}_{lm}^{\ast }({\hat{\mathbf{r}}}^{\prime })Y_{lm}(\hat{\mathbf{r}})$$

考虑另一个球坐标系 $(\tilde{r},\tilde{\theta },\tilde{\phi })$ ，它的 $\tilde{\theta }=0$ 轴沿 ${\mathbf{r}}^{\prime }$ 方向。由于 $\mathbf{r},{\mathbf{r}}^{\prime }$ 的夹角为 $\gamma$ ，新坐标系下

$$\mathbf{r}=(|\mathbf{r}-{\mathbf{r}}^{\prime }|,\gamma ,\ast {)}_{\tilde{r}\tilde{\theta }\tilde{\phi }}$$

问题关于 $\tilde{\phi }$ 有旋转对称性， $\tilde{\phi }$ 为任意值。

而 $\frac{1}{|\mathbf{r}-{\mathbf{r}}^{\prime }|}$ 正好是 $P_l(x)$ 的 生成函数 。所以就有

$$\frac{1}{|\mathbf{r}-{\mathbf{r}}^{\prime }|}=\sum _{l=0}^{+\infty }\frac{r_{<}^l}{r_{>}^{l+1}}{P}_l(\cos \gamma )$$

利用球谐函数展开的唯一性，比较系数就发现 $l$ 次 Legendre 多项式可以用 $2l+1$ 项球谐函数乘积的和式表出

$$P_l(\cos \gamma )=\frac{4\pi }{2l+1}\sum _{m=-l}^{+l}{Y}_{lm}^{\ast }({\mathbf{n}}^{\prime })Y_{lm}(\mathbf{n})$$
其中 $\gamma =⟨\mathbf{r},{\mathbf{r}}^{\prime }⟩=⟨\mathbf{n},{\mathbf{n}}^{\prime }⟩$ 。

作为 $\mathbf{n}={\mathbf{n}}^{\prime }$ （从而 $P_l(\cos \gamma )=P_l(1)=1$ ）的特殊情况：

$$\sum _{m=-l}^{+l}{Y}_{lm}^{\ast }(\mathbf{n})Y_{lm}(\mathbf{n})=\frac{2l+1}{4\pi }$$

证明

一个巧妙的证明利用到

$\frac{1}{|\mathbf{r}-{\mathbf{r}}^{\prime }|}$ 是 Poisson 方程 ${\nabla }^{2}u=-4\pi f(\mathbf{r})$ 的格林函数

这一事实。

具体地，已知 $G(\mathbf{r};{\mathbf{r}}^{\prime })=\frac{1}{|\mathbf{r}-{\mathbf{r}}^{\prime }|}$ 是方程 ${\nabla }^{2}G(\mathbf{r};{\mathbf{r}}^{\prime })=-4\pi {\delta }^{(3)}(\mathbf{r}-{\mathbf{r}}^{\prime })$ 的解。其中 ${\delta }^{(3)}(\mathbf{r}-{\mathbf{r}}^{\prime })$ 可以展开为

$${\delta }^{(3)}(\mathbf{r}-{\mathbf{r}}^{\prime })=\frac{1}{r^2}\delta (r-r^{\prime })\delta (\cos \theta -\cos {\theta }^{\prime })\delta (\phi -{\phi }^{\prime })$$
故也将 Green 函数展开为

$$\frac{1}{|\mathbf{r}-{\mathbf{r}}^{\prime }|}\equiv G(\mathbf{r};{\mathbf{r}}^{\prime })=\sum _{l=0}^{+\infty }\sum _{m=-l}^{+l}{g}_{lm}(r;r^{\prime })Y_{lm}^{\ast }({\mathbf{n}}^{\prime })Y_{lm}(\mathbf{n})$$

$g_{lm}$ 是和角向变量无关的展开系数。代入 Green 函数满足的方程，得到

$$\frac{1}{r}\frac{{\mathrm{d}}^2}{\mathrm{d}{r}^2}[r{g}_{lm}(r;r^{\prime })]-\frac{l(l+1)}{r^2}{g}_{lm}(r;r^{\prime })=-\frac{4\pi }{r^2}\delta (r-r^{\prime })$$

1. 上述方程和参数 $m$ 无关，故 $g_{lm}\equiv g_l$
2. $r\ne r^{\prime }$ 时上述常微分方程方程齐次，要么 $g_l\sim r^l$ 要么 $g_l\sim r^{-l-1}$
3. 对于给定的 $r^{\prime }$ ， $g_l(r;r^{\prime })$ 在 $r\to 0$ 和 $r\to \infty$ 时应该有界。联系2就得到

$$g_l(r;r^{\prime })=A_l\frac{r_{<}^l}{r_{>}^{l+1}}=\{\begin{array}{ll}\frac{A_l}{r^{\prime }}{\left(\frac{r}{r^{\prime }}\right)}^l,& 0\le r<r^{\prime }\\ \frac{A_l}{r}{\left(\frac{r^{\prime }}{r}\right)}^l,& r\ge r^{\prime }\end{array}$$

有界：考虑 $g_l$ 的物理含义？

最后用连接条件

$$\frac{\mathrm{d}[r{g}_l(r;r^{\prime })]}{\mathrm{d}r}{|}_{r=r^{\prime }-\epsilon }^{r=r^{\prime }+\epsilon }=-\frac{4\pi }{r^{\prime }}$$

定出 $A_l=\frac{4\pi }{2l+1}$ 。这样就证明了加法定理。

最后

以上就是飘逸龙猫为你收集整理的电动力学的数学准备 01 球函数和球谐函数Legendre 多项式连带 Legendre 函数球谐函数的全部内容，希望文章能够帮你解决电动力学的数学准备 01 球函数和球谐函数Legendre 多项式连带 Legendre 函数球谐函数所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。