文章目录
- 一、机器学习简述
- 机器学习算法分类
- 机器学习开发流程
- 二、数据划分、转换器、估计器
- sklearn 内置数据集
- 数据集进行分割
- 转换器与预估器
- 三、K-近邻算法(KNN)
- 核心思想
- KNN 算法 API
- 案例分析
- 优缺点分析
- 四、朴素贝叶斯(Bayes)
- 核心思想
- Bayes算法API
- 案例分析
- 优缺点分析
- 五、决策树与随机森林
- ①决策树
- 核心思想
- 决策树 API
- 案例分析
- 优缺点分析
- ②随机森林
- 核心思想
- 随机森林 API
- 案例分析
- 随机森林的优点
- 六、分类模型的准确性评估
一、机器学习简述
机器学习算法分类
监督学习(预测):数据集有特征值+目标值
- 分类(目标值离散型)——K-近邻算法、贝叶斯分类、决策树与随机森林、逻辑回归、神经网络
- 回归(目标值连续型)——线性回归、岭回归
- 标注——隐形马尔科夫模型
非监督学习(聚类):数据集只有特征值
- 聚类——K-Means 算法
机器学习开发流程
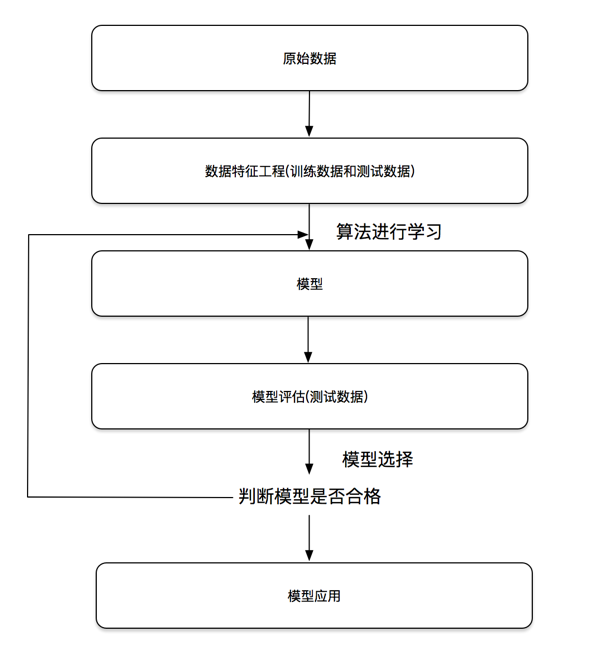
- 建立模型,根据数据类型划分应用种类,根据原始数据明确问题做什么;
- 数据的基本处理:pd 数据去重,合并表等等;
- 建立特征工程,对特征进行处理;
- 选择相应算法进行分析;
- 模型的评估,判定效果,直到模型合格;
- 模型上线使用,以 API 形式提供;
二、数据划分、转换器、估计器
sklearn 内置数据集
数据集划分
- 训练集(70%-80%):建立模型
- 测试集(30%-20%):评估模型
- 划分 API:sklearn.model_seletion.train_test_split
sklearn 数据集接口介绍
-
sklearn.datasets:加载获取流行数据集
-
datasets.load_*():获取小规模数据集,数据包含在 datasets 里
-
datasets.fetch_*(data_home=None):data_home参数代表数据集下载的目录,下载后的默认路径是~/scikit_learn_data/
-
返回数据类型:datasets.base.Bunch(字典格式)
-
data:特征数据数组,是二维 np.ndarray 数据
-
target:标签数组,是 n_samples 的一维数组
-
DESCR:数据描述
-
feature_names:特征名(新闻数据、手写数字、回归数据集没有特征名)
-
target_names:标签名
sklearn 分类数据集
from sklearn.datasets import load_iris()
sklearn 回归数据集
from sklearn.datasets import load_boston()
数据集进行分割
sklearn.model_selection.train_test_split(x,y,test_size,random_state)
参数解释
- x:数据集的特征值
- y:数据集的标签值
- test_size :测试集的大小,一般为float
- random_state :随机数种子,不同的种子会造成不同的随机采样结果,相同的种子采样结果相同。
- 返回值:x_train,x_test,y_train,y_test,lable(返回的顺序固定)
转换器与预估器
转换器
fit_transform():输入数据直接转换;
fit():输入数据,计算平均值、方差等,但不转换;
transform():转换数据;
估计器
在 sklearn 中,估计器(estimator)是一个重要的角色,是一类实现了算法的 API;
-
用于分类的估计器:
-
sklearn.neighbors K-近邻算法
-
sklearn.naive_bayes 贝叶斯算法
-
sklearn.linear_model.LogisticRegression 逻辑回归
-
sklearn.tree 决策树与随机森林
-
用于回归的估计器:
-
sklearn.linear_model.LinearRegression 线性回归
-
sklearn.linear_model.Ridge 岭回归
三、K-近邻算法(KNN)
核心思想
如果一个样本在特征空间中的 k 个最相似(即特征空间中最邻近)的样本中的大多数来自某一个类别,则该样本也属于这个类别;KNN 算法需要做标准化处理;
两个样本的距离可以通过欧式距离衡量:
欧式距离公式:
- ( a 1 − b 1 ) 2 + ( a 2 − b 2 ) 2 + . . . ( a n − b n ) 2 sqrt{(a_1-b_1)^2+(a_2-b_2)^2+...(a_n-b_n)^2} (a1−b1)2+(a2−b2)2+...(an−bn)2
KNN 算法 API
-
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm='auto') -
n_neighbors:整数 int 型,可选(默认= 5),k_neighbors查询默认使用的邻居数 ;
-
algorithm:{‘auto’,‘ball_tree’,‘kd_tree’,‘brute’},可选用于计算最近邻居的算法:‘ball_tree’将会使用 BallTree,‘kd_tree’将使用 KDTree。‘auto’将尝试根据传递给fit方法的值来决定最合适的算法。 (不同实现方式影响效率)
案例分析
数据地址:链接:https://pan.baidu.com/s/1kvqPSyfRw0ZYCQZbCMadfA 密码:9vc3
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
#KNN预测模拟Facebook用户签到位置
def knncls1():
#读取数据
data=pd.read_csv('train.csv')
#处理数据,减少数据的量用于测试
data = data.query("x > 1.0 & x < 1.25 & y > 2.5 & y < 2.75")
#1.处理时间戳
time_value=pd.to_datetime(data['time'],unit='s')
time_value=pd.DatetimeIndex(time_value)
#2.构造时间特征
data['day']=time_value.day
data['hour']=time_value.hour
#3.删除无用的特征
data=data.drop(['time'],axis=1)
#4.删除签到次数较少的地址
place_count = data.groupby('place_id').count()
tf=place_count[place_count.row_id>3].reset_index()
data=data[data['place_id'].isin(tf.place_id)]
#取出数据当中的特征值和目标值
y=data['place_id']
x=data[['x','y','accuracy']]
#将数据分割为训练集和测试集
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.25)
#特征工程(标准化)
std=StandardScaler()
x_train=std.fit_transform(x_train)
x_test=std.transform(x_test)
#KNN算法流程
#1.实例化 KNN
knn=KNeighborsClassifier(n_neighbors=3)
knn.fit(x_train,y_train)
#2.得出预测结果
y_predict=knn.predict(x_test)
print('KNN预测目标入住位置为:',y_predict)
#3.得出准确率
print('预测的准确率:',knn.score(x_test,y_test))
return None
#运行程序
knncls1()
[out]:
KNN预测目标入住位置为: [3312463746 3992589015 7098464262 ... 6683426742 6237569496 6889790653]
预测的准确率: 0.49858156028368794
优缺点分析
-
优点
简单、易于理解、易于实现,无需参数估计,无需训练; -
缺点
K 值取值问题
- K 值取很小:容易受异常值影响
- K 值取很小:容易受 K值数量(类别)的波动
性能问题
- 由于每两个样本之间都需要计算欧式空间距离,时间复杂度高,所以 KNN 算法计算性能较差;
-
使用场景
- 小数据场景,几千~几万样本区间使用效果较好;
四、朴素贝叶斯(Bayes)
核心思想
1.相关术语介绍
①联合概率:包含多个条件,且所有条件同时成立的概率。
公式:
P
(
A
,
B
)
=
P
(
A
)
∗
P
(
B
)
P(A,B)=P(A)*P(B)
P(A,B)=P(A)∗P(B)
②条件概率:事件A在另一个事件B已经发生的条件下发生的概率。记作
P
(
A
∣
B
)
P(A|B)
P(A∣B)
当
A
1
,
A
2
A1,A2
A1,A2 相互独立时:
P
(
A
1
,
A
2
∣
B
)
=
P
(
A
1
∣
B
)
∗
P
(
A
2
∣
B
)
P(A1,A2|B)=P(A1|B)*P(A2|B)
P(A1,A2∣B)=P(A1∣B)∗P(A2∣B)
2.使用场景
一般用于文档分类场景,当特征独立时使用;
3.贝叶斯公式
对于文档分类模型,可以理解为:
P
(
C
∣
W
)
=
P
(
W
∣
C
)
P
(
C
)
P
(
W
)
P(C|W)=frac{P(W|C)P(C)}{P(W)}
P(C∣W)=P(W)P(W∣C)P(C)
其中 W 为给定文档的特征值(频数统计,预测文档提供),C 为文档类别;
公式可以理解为:
P
(
C
∣
F
1
,
F
2
,
.
.
.
)
=
P
(
F
1
,
F
2
,
.
.
.
∣
C
)
P
(
C
)
P
(
F
1
,
F
2
,
.
.
.
)
P(C|F1,F2,...)=frac{P(F1,F2,...|C)P(C)}{P(F1,F2,...)}
P(C∣F1,F2,...)=P(F1,F2,...)P(F1,F2,...∣C)P(C)
其中 C 可以是不同类别;
公式分为三部分:
- P ( C ) P(C) P(C):每个文档类别的概率(某类别文档数/总文档数)
-
P
(
W
∣
C
)
P(W|C)
P(W∣C):给定类别下特征(被预测文档出现的词)的概率
计算方法: P ( F 1 ∣ C ) = N i / N P(F1|C)=N_i/N P(F1∣C)=Ni/N
N i N_i Ni为该 F 1 F1 F1 词在 C C C类别所有文档中出现的次数;
N N N为所属类别 C C C下的文档所有词出现的次数和; - P ( F 1 , F 2 , . . . ) P(F1,F2,...) P(F1,F2,...):预测文档中每个词的概率
4.算法思想案例分析
给定的预测文档如下,根据词频已统计出重要性较高的四个词语:
| 特征/统计 | 科技类别(30篇) | 娱乐类别(60篇) | 汇总(90 篇) |
|---|---|---|---|
| ‘商场’ | 9 | 51 | 60 |
| ‘影院’ | 8 | 56 | 64 |
| ‘支付宝’ | 20 | 15 | 35 |
| ‘云计算’ | 63 | 0 | 63 |
| 汇总 | 100 | 121 | 221 |
即在已给出类别的训练文档中,‘商场’一词在 9 篇科技文档中出现,在‘51 ’篇娱乐文档中出现;
现有一篇预测文档,出现了‘影院’,‘支付宝’,‘云计算’等词,求其分别属于科技和娱乐的概率;
- 属于科技类别的概率求法:
P ( 科 技 ∣ 影 院 , 支 付 宝 , 云 计 算 ) P(科技|影院,支付宝,云计算) P(科技∣影院,支付宝,云计算)
=
P
(
影
院
,
支
付
宝
,
云
计
算
∣
科
技
)
∗
P
(
科
技
)
P
(
影
院
,
支
付
宝
,
云
计
算
)
=frac{P(影院,支付宝,云计算|科技)*P(科技)}{P(影院,支付宝,云计算)}
=P(影院,支付宝,云计算)P(影院,支付宝,云计算∣科技)∗P(科技)
=
P
(
影
院
∣
科
技
)
∗
P
(
支
付
宝
∣
科
技
)
∗
P
(
云
计
算
∣
科
技
)
∗
P
(
科
技
)
P
(
影
院
,
支
付
宝
,
云
计
算
)
=frac{P(影院|科技)*P(支付宝|科技)*P(云计算|科技)*P(科技)}{P(影院,支付宝,云计算)}
=P(影院,支付宝,云计算)P(影院∣科技)∗P(支付宝∣科技)∗P(云计算∣科技)∗P(科技)
=
9
100
∗
20
100
∗
63
100
∗
30
90
∗
1
P
(
影
院
,
支
付
宝
,
云
计
算
)
=frac{9}{100}*frac{20}{100}*frac{63}{100}*frac{30}{90}*frac{1}{P(影院,支付宝,云计算)}
=1009∗10020∗10063∗9030∗P(影院,支付宝,云计算)1
- 属于娱乐类别的概率求法:
P ( 娱 乐 ∣ 影 院 , 支 付 宝 , 云 计 算 ) P(娱乐|影院,支付宝,云计算) P(娱乐∣影院,支付宝,云计算)
=
P
(
影
院
,
支
付
宝
,
云
计
算
∣
娱
乐
)
∗
P
(
娱
乐
)
P
(
影
院
,
支
付
宝
,
云
计
算
)
=frac{P(影院,支付宝,云计算|娱乐)*P(娱乐)}{P(影院,支付宝,云计算)}
=P(影院,支付宝,云计算)P(影院,支付宝,云计算∣娱乐)∗P(娱乐)
=
P
(
影
院
∣
娱
乐
)
∗
P
(
支
付
宝
∣
娱
乐
)
∗
P
(
云
计
算
∣
娱
乐
)
∗
P
(
娱
乐
)
P
(
影
院
,
支
付
宝
,
云
计
算
)
=frac{P(影院|娱乐)*P(支付宝|娱乐)*P(云计算|娱乐)*P(娱乐)}{P(影院,支付宝,云计算)}
=P(影院,支付宝,云计算)P(影院∣娱乐)∗P(支付宝∣娱乐)∗P(云计算∣娱乐)∗P(娱乐)
=
56
121
∗
15
121
∗
0
121
∗
60
90
∗
1
P
(
影
院
,
支
付
宝
,
云
计
算
)
=frac{56}{121}*frac{15}{121}*frac{0}{121}*frac{60}{90}*frac{1}{P(影院,支付宝,云计算)}
=12156∗12115∗1210∗9060∗P(影院,支付宝,云计算)1
-
此处由于给定的分类文章中,所有娱乐类别都不含‘云计算’,故 P ( 云 计 算 ∣ 娱 乐 ) P(云计算|娱乐) P(云计算∣娱乐)为0,导致 P ( 娱 乐 ∣ 影 院 , 支 付 宝 , 云 计 算 ) P(娱乐|影院,支付宝,云计算) P(娱乐∣影院,支付宝,云计算)最终计算结果为 0,影响结果,实际操作时,应使用拉普拉斯平滑系数来避免这类情况发生。
-
且上述概率计算中,都有相同的数 1 P ( 影 院 , 支 付 宝 , 云 计 算 ) frac{1}{P(影院,支付宝,云计算)} P(影院,支付宝,云计算)1,而朴素贝叶斯的思想最终只需要比较各类别概率的大小,这部分一般可不计算。
5.拉普拉斯平滑系数
P
(
F
1
∣
C
)
=
N
i
+
α
N
+
α
m
P(F1|C)=frac{N_i+alpha}{N+alpha m}
P(F1∣C)=N+αmNi+α
α
alpha
α为指定的系数,一般默认为1,
m
m
m 为训练文档中统计出的特征词个数。
则上述案例中预测文档属于娱乐类别的概率求法应为:
P
(
影
院
∣
娱
乐
)
∗
P
(
支
付
宝
∣
娱
乐
)
∗
P
(
云
计
算
∣
娱
乐
)
∗
P
(
娱
乐
)
P
(
影
院
,
支
付
宝
,
云
计
算
)
frac{P(影院|娱乐)*P(支付宝|娱乐)*P(云计算|娱乐)*P(娱乐)}{P(影院,支付宝,云计算)}
P(影院,支付宝,云计算)P(影院∣娱乐)∗P(支付宝∣娱乐)∗P(云计算∣娱乐)∗P(娱乐)
=
56
+
1
121
+
1
∗
4
∗
15
+
1
121
+
1
∗
4
∗
0
+
1
121
+
1
∗
4
∗
60
90
∗
1
P
(
影
院
,
支
付
宝
,
云
计
算
)
=frac{56+1}{121+1*4}*frac{15+1}{121+1*4}*frac{0+1}{121+1*4}*frac{60}{90}*frac{1}{P(影院,支付宝,云计算)}
=121+1∗456+1∗121+1∗415+1∗121+1∗40+1∗9060∗P(影院,支付宝,云计算)1
Bayes算法API
-
sklearn.naive_bayes.MultinomiaNB(alpha=1.0) - alpha:拉普拉斯平滑系数
案例分析
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
def naivebayes():
#导入数据
from sklearn.datasets import fetch_20newsgroups
news=fetch_20newsgroups(subset=all)
#进行数据分割
x_trains,x_test,y_train,y_test=train_test_split(news.data,news.target,test_size=0.25)
#训练集中特征获取
tf=TfidfVectorizer()
#以训练集中特征抽取出来的词语统计测试集数据
x_trains=tf.fit_transform(x_trains)
x_test=tf.transform(x_test)
#朴素贝叶斯算法预测
mlt=MultinomialNB(alpha=1.0)
mlt.fit(x_trains,y_train)
print('朴素贝叶斯预测的文章类别为:')
y_predict=mlt.predict(x_test)
print('朴素贝叶斯估计预测的准确率为:',mlt.score(x_test,y_test))
print(news)
return None
naivebayes()
- 此处20newsgroups存在下载速度非常慢的情况,Win 系统解决方法参考:
https://blog.csdn.net/u012620645/article/details/47080745
优缺点分析
-
优点
-
朴素贝叶斯模型发源于古典数学理论,模型稳定,分类效率较高;
-
对于缺失数据不敏感,算法也较为简单,常用于文本分类;
-
分类精确度高,速度快;
-
缺点
-
由于使用了样本属性独立性的假设,所以如果样本属性有关联时,使用效果不好;
-
非常依赖于训练集样本给定的精确度,若训练集误差较大,则效果肯定不好;
五、决策树与随机森林
①决策树
核心思想
决策树来源思想即程序设计中的if-then 结构,由决策树的根节点到叶节点的路径构成一条规则;
-
决策树学习算法通常是递归地选择最优特征(注:从所有可能的决策树模型中选择最优决策树是NP完全问题,通常我们得到的决策树是次最优的,即不一定是全局最优,而是在每一个节点处做到最优,决策树的构建属于贪心策略)
-
信息、熵以及信息增益的概念
这三个基本概念是决策树的根本,是决策树利用特征来分类时,确定特征选取顺序的依据。理解了它们,决策树你也就了解了大概。
引用香农的话来说,信息是用来消除随机不确定性的东西。当然这句话虽然经典,但是还是很难去搞明白这种东西到底是个什么样,可能在不同的地方来说,指的东西又不一样。对于机器学习中的决策树而言,如果带分类的事物集合可以划分为多个类别当中,则某个类( x i xi xi)的信息可以定义如下:
I ( X = x i ) = − l o g 2 p ( x i ) I(X=x_i)=-log_2p(x_i) I(X=xi)=−log2p(xi)
H ( X ) = Σ x ∈ X P ( x ) l o g P ( x ) H(X)=Sigma_{xin X}P(x)logP(x) H(X)=Σx∈XP(x)logP(x)
- I ( X ) I(X) I(X)用来表示随机变量的信息, p ( x i ) p(x_i) p(xi)指是当 x i x_i xi发生时的概率。
- 熵 H ( X ) H(X) H(X)是用来度量不确定性的,当熵越大, X = x i X=x_i X=xi的不确定性越大,反之越小。对于机器学习中的分类问题而言,熵越大即这个类别的不确定性更大,反之越小。
- 信息增益在决策树算法中是用来选择特征的指标,信息增益越大,则这个特征的选择性越好。
在决策树算法中:
- ID3基于信息增益作为属性选择的度量;
- C4.5基于信息增益作为属性选择的度量;
- CART基于基尼指数作为属性选择的度量;
决策树 API
-
class sklearn.tree.DecisionTreeClassifier(criterion=’gini’, max_depth=None,random_state=None) - criterion:默认是’gini’系数,也可以选择信息增益的熵’entropy’
- max_depth:树的深度大小
- random_state:随机数种子
案例分析
def decision():
#决策树对泰坦尼克号生死进行预测
#获取数据
titanic=pd.read_csv('http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt')
#处理数据,找出特征值和目标值
x=titanic[['pclass','sex','age']]
y=titanic['survived']
#处理缺失值
x['age'].fillna(x['age'].mean(),inplace=True)
#数据分割为训练集和测试集
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.25)
#进行特征工程处理,进行 one—hot 编码(由于 age 和 sex 为类别类型)
#1.导入API
from sklearn.feature_extraction import DictVectorizer
dict=DictVectorizer(sparse=False)
x_train=dict.fit_transform(x_train.to_dict(orient='records'))
x_test=dict.transform(x_test.to_dict(orient='records'))
#决策树算法预测
from sklearn.tree import DecisionTreeClassifier
dec = DecisionTreeClassifier(max_depth=5)
dec.fit(x_train,y_train)
#预测准确率
print('决策树预测准确率为:',dec.score(x_test,y_test))
#导出决策树的结构
import matplotlib.pyplot as plt
from sklearn import tree
from sklearn.tree import plot_tree
plt.figure(figsize=(100,100))
_ = tree.plot_tree(dec,filled = True,max_depth=5)
plt.savefig('./tree.jpg')
decision()
- 作者注: 0.20版本以上的scikit-learn 库中更新了关于决策树结构绘制的包,可直接导入相关的包使用;
from sklearn.tree import plot_tree
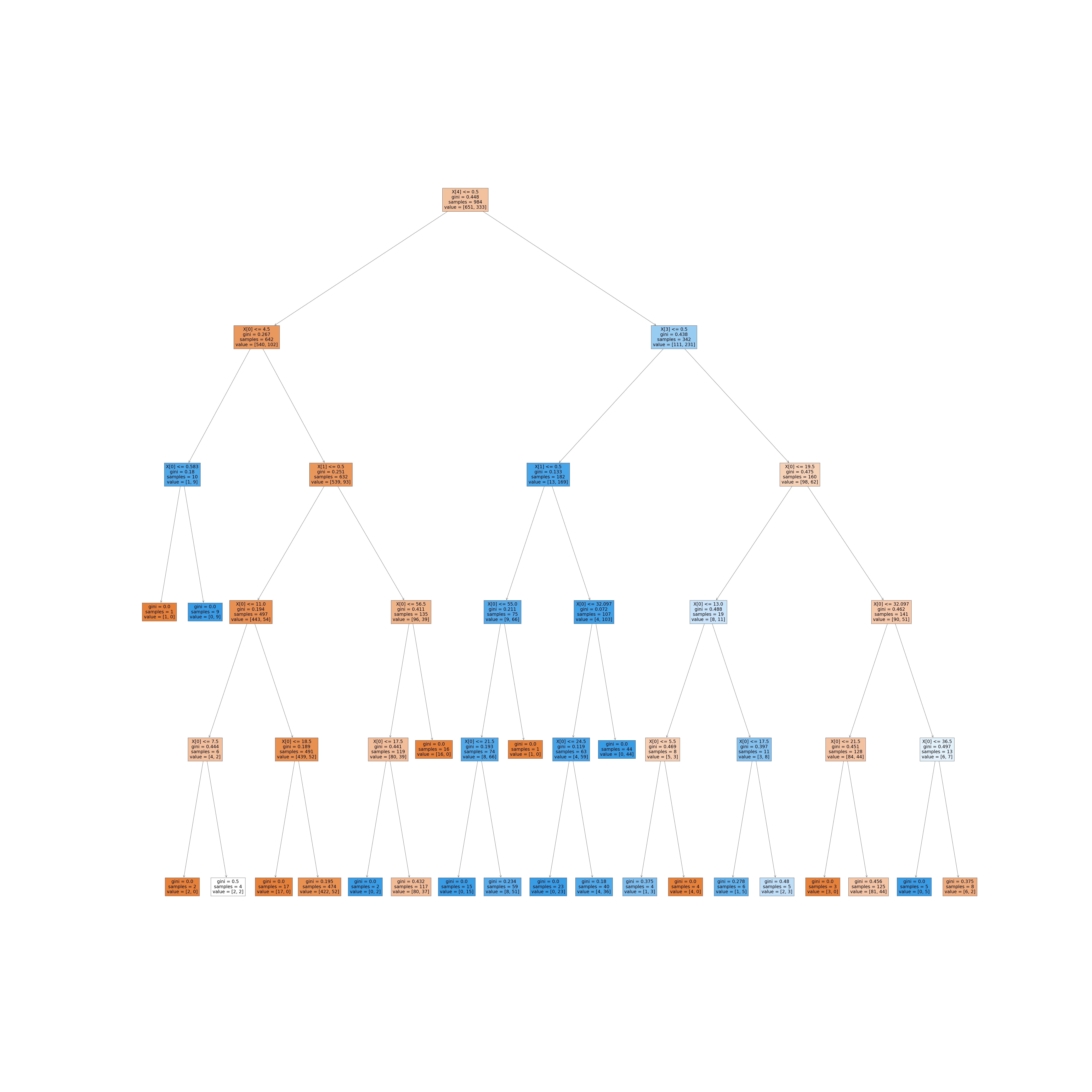
优缺点分析
-
优点
-
简单的理解和解释,树木可视化
-
需要很少的数据准备,其他技术通常需要数据归一化;
-
缺点
-
决策树学习者可以创建不能很好地推广数据的过于复杂的树,容易被过拟合;
-
改进方法
-
减枝cart 算法(在决策树 API 中已经实现)
-
随机森林
②随机森林
核心思想
随机森林就是通过集成学习的思想将多棵树集成的一种算法,它的基本单元是决策树,而它的本质属于机器学习的一大分支——集成学习(Ensemble Learning)方法。
其实从直观角度来解释,每棵决策树都是一个分类器(假设现在针对的是分类问题),那么对于一个输入样本,N棵树会有N个分类结果。而随机森林集成了所有的分类投票结果,将投票次数最多的类别指定为最终的输出,这就是一种最简单的 Bagging 思想。
每棵树的按照如下规则生成:
- 1)指定单个决策树训练集大小为N,对于每棵树而言,随机且有放回地从总训练集中的抽取N个训练样本(这种采样方式称为bootstrap sample方法),作为该树的训练集;
从这里我们可以知道:每棵树的训练集都是随机的,训练样本有可能是重复。
为什么要随机抽样训练集?
如果不进行随机抽样,每棵树的训练集都一样,那么最终训练出的树分类结果也是完全一样的,这样的话完全没有bagging的必要;
为什么要有放回地抽样?
如果不是有放回的抽样,那么每棵树的训练样本都是不同的,都是没有交集的,这样每棵树都是"有偏的",都是绝对"片面的"(当然这样说可能不对),也就是说每棵树训练出来都是有很大的差异的;而随机森林最后分类取决于多棵树(弱分类器)的投票表决,这种表决应该是"求同",因此使用完全不同的训练集来训练每棵树这样对最终分类结果是没有帮助的,这样无异于是"盲人摸象"。
-
2)如果每个样本的特征维度为M,指定一个常数m<<M,随机地从M个特征中选取m个特征子集,每次树进行分裂时,从这m个特征中选择最优的;
-
3)每棵树都尽最大程度的生长,并且没有剪枝过程。
一开始我们提到的随机森林中的“随机”就是指的这里的两个随机性。两个随机性的引入对随机森林的分类性能至关重要。由于它们的引入,使得随机森林不容易陷入过拟合,并且具有很好得抗噪能力(比如:对缺省值不敏感)。
随机森林 API
-
class sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True, random_state=None)
参数解释 - n_estimators:integer,optional(default = 10) 森林里的树木数量(一般可选 120,200,300,500,800,1200);
- criteria:string,可选(default =“gini”)分割特征的测量方法;
- max_depth:integer或None,可选(默认=无)树的最大深度 ;
- bootstrap:boolean,optional(default = True)是否在构建树时使用放回抽样 ;
- max_features=‘auto’,‘sqrt’,‘log2’,None:每个决策树的最大特征数量
‘auto’:最大特征数量=sqrt(n_features)
‘sqrt’:最大特征数量=sqrt(n_features),跟 auto 一致;
‘log2’:最大特征数量=log2(n_features)
None:最大特征数量=n_features
案例分析
def RandomForest():
#随机森林对泰坦尼克号生死进行预测
#获取数据
titanic=pd.read_csv('http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt')
#处理数据,找出特征值和目标值
x=titanic[['pclass','sex','age']]
y=titanic['survived']
#处理缺失值
x['age'].fillna(x['age'].mean(),inplace=True)
#数据分割为训练集和测试集
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.25)
#进行特征工程处理,进行 one—hot 编码(由于 age 和 sex 为类别类型)
#1.导入API
from sklearn.feature_extraction import DictVectorizer
dict=DictVectorizer(sparse=False)
x_train=dict.fit_transform(x_train.to_dict(orient='records'))
x_test=dict.transform(x_test.to_dict(orient='records'))
#随机森林算法预测
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier()
rf.fit(x_train,y_train)
#网格搜索+交叉验证
from sklearn.model_selection import GridSearchCV
param={'n_estimators':[120,200,300,500,1200],'max_depth':[5,8,10,20,30]}
gc=GridSearchCV(rf,param_grid=param,cv=5)
gc.fit(x_train,y_train)
#交叉检验预测结果
print('准确率:',gc.best_score_)
print('最好的参数:',gc.best_estimator_)
RandomForest()
[out]:
准确率: 0.8363821138211383
最好的参数: RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=5, max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=200, n_jobs=None,
oob_score=False, random_state=None, verbose=0,
warm_start=False)
随机森林的优点
- 当前所有算法中,具有极高的准确率;
- 能够有效运行在大数据集中;
- 能够处理具有高维度的输入样本,而且不需要降维;
- 能够评估各个特征在分类问题上的重要性;
六、分类模型的准确性评估
①预测准确率
estimator.score(),即预测结果正确的样本占总样本的百分比;
②精确率&召回率
在分类任务下,对于一个预测结果(Predict Condition)与正确标记(True Condition)之间存在四种不同的组合,构成混淆矩阵;
| 预测正例 | 预测假例 | |
|---|---|---|
| 真实正例 | 真正例TP(True Positive) | 伪反例FN(False Negative) |
| 真实假例 | 伪正例FP(False Positive) | 真反例TN(True Negative) |
由此引入两个概念:
-
精确率(Precision):预测结果为正例的样本中,真实为正例的比例(即是否查的准)
-
召回率(Recall):真实为正例的样本中,预测结果为正例的比例(即是否查的全)
-
其他分类标准, F 1 − s c o r e F1-score F1−score,反映了模型的稳健性
F 1 = 2 T P 2 T P + F N + F P = 2 ∗ P r e c i s i o n ∗ R e c a l l P r e c i s i o n + R e c a l l F1=frac{2TP}{2TP+FN+FP}=frac{2*Precision*Recall}{Precision+Recall} F1=2TP+FN+FP2TP=Precision+Recall2∗Precision∗Recall -
分类评估 API
sklearn.metrics.classification_report(y_true,y_pred,target_names=None) -
y_true: 真实目标值
-
y_pred: 估计器预测目标值
-
target_names:目标类别名称
-
返回值:每个类别精确率和召回率
③模型选择与调优
- 交叉验证:为了让被评估的模型更加准确可信;
交叉验证的思想是将训练集中的所有数据分为 N 等份,交叉检验得到 N 个准确率,最后求出平均准确率。
注:以下所有数据均来自训练集;
| 1 | 2 | 3 | … | N | 结果 |
|---|---|---|---|---|---|
| 验证集 | 训练集1 | 训练集2 | … | 训练集N-1 | 模型 1+准确度 1 |
| 训练集1 | 验证集 | 训练集2 | … | 训练集N-1 | 模型 2+准确度 2 |
| 训练集1 | 训练集2 | 验证集 | … | 训练集N-1 | 模型 3+准确度 3 |
| … | … | … | … | … | … |
| 训练集1 | 训练集2 | 训练集3 | … | 验证集 | 模型 N+准确度 N |
最后,根据上述1~N个模型准确度计算最终的平均准确度
-
网格搜索
也称为超参数搜索,通常情况下有很多参数是需要手动指定(如 k-近邻算法中的k值),但手动调参数过程较为繁复,所以需要对模型预设几种超参数组合,每一组超参数组合都使用交叉检验来进行评估,最后选出最优的参数组合建立模型;网格搜索API
sklearn.model_selection.GridSearchCV(estimator, param_grid=None,cv=None)参数解释:
- estimator:估计器对象
- param_grid:估计器参数(dict){“n_neighbors”:[1,3,5]}
- cv:指定几折交叉验证
- fit:输入训练数据
- score:准确率
返回结果:
- best_score_:在交叉验证中测试的最好结果
- best_estimator_:最好的参数模型
- cv_results_:每次交叉验证后的验证集准确率结果和训练集准确率结果
KNN算法超参数搜索案例
import pandas as pd
import numpy as np
#导入超参数网格搜索 API
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
#KNN预测模拟Facebook用户签到位置
def knncls():
data=pd.read_csv('train.csv')
data = data.query("x > 1.0 & x < 1.25 & y > 2.5 & y < 2.75")
time_value=pd.to_datetime(data['time'],unit='s')
time_value=pd.DatetimeIndex(time_value)
data['day']=time_value.day
data['hour']=time_value.hour
place_count = data.groupby('place_id').count()
tf=place_count[place_count.row_id>3].reset_index()
data=data[data['place_id'].isin(tf.place_id)]
y=data['place_id']
x=data[['x','y','accuracy','day','hour']]
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.25)
std=StandardScaler()
x_train=std.fit_transform(x_train)
x_test=std.transform(x_test)
#KNN算法流程
#此处不需要填写超参数
knn=KNeighborsClassifier()
knn.fit(x_train,y_train)
y_predict=knn.predict(x_test)
print('在测试集上的准确率:',knn.score(x_test,y_test))
#构造一些参数值进行搜索
param={'n_neighbors':[3,5,7]}
#进行网格搜索
gc=GridSearchCV(knn,param_grid=param,cv=2)
gc.fit(x_train,y_train)
#返回超参数网格搜索及交叉验证结果
print('在交叉验证中最好的结果:',gc.best_score_)
print('最好的参数模型是:',gc.best_estimator_)
print('每个超参数每次交叉验证的结果',gc.cv_results_)
return None
#运行程序
knncls()
最后
以上就是勤恳秋天最近收集整理的关于机器学习—分类算法(KNN、Bayes、Tree、RandomForest算法详解)一、机器学习简述二、数据划分、转换器、估计器三、K-近邻算法(KNN)四、朴素贝叶斯(Bayes)五、决策树与随机森林六、分类模型的准确性评估的全部内容,更多相关机器学习—分类算法(KNN、Bayes、Tree、RandomForest算法详解)一、机器学习简述二、数据划分、转换器、估计器三、K-近邻算法(KNN)四、朴素贝叶斯(Bayes)五、决策树与随机森林六、分类模型内容请搜索靠谱客的其他文章。








发表评论 取消回复