课后自主练习（递归）1057. 波兰表达式 easy《编程思维与实践》个人学习笔记

题目

逆波兰式是计算机专业常用的表达式，又称后缀表达式。反过来，把运算符前置的算术表达式则称为波兰式，或前缀表达式。

例如普通的表达式的波兰表示法为2+3：+ 2 3。波兰表达式的优点也是运算符之间不必有优先级关系，也不必用括号改变运算次序 .

例如：(2 + 3) * 4的波兰式为：* + 2 3 4，而5-6*7 的波兰表达式为：- 5 * 6 7。

现给定一个波兰表达式，请编写程序计算该表达式的值。

注意：波兰表达式中的运算符包括+ - * / 四个。

数据
3

+ 2 0
- 0.5 3
* + 2 3 4

答案
case #0:
2.000000
case #1:
-2.500000
case #2:
20.000000

思路

既然用到了波兰表达式，我们可以利用deque来实现数据的储存和转换
首先，数据自然是全部都存放进去
然后使用的时候碰到一个运算符号（±×÷）就要开两个栈来预留给两个数字，然后如果继续遇到运算符号继续预留两个数字，直到遇到两个数字，进行运算后返回到上一个栈中，上一个栈对应的另一个子栈再找一个数字来和原先的子栈进行计算即可

说的比较抽象我们就拿图来说
比如+ 5 * - 6 / 4 2 3

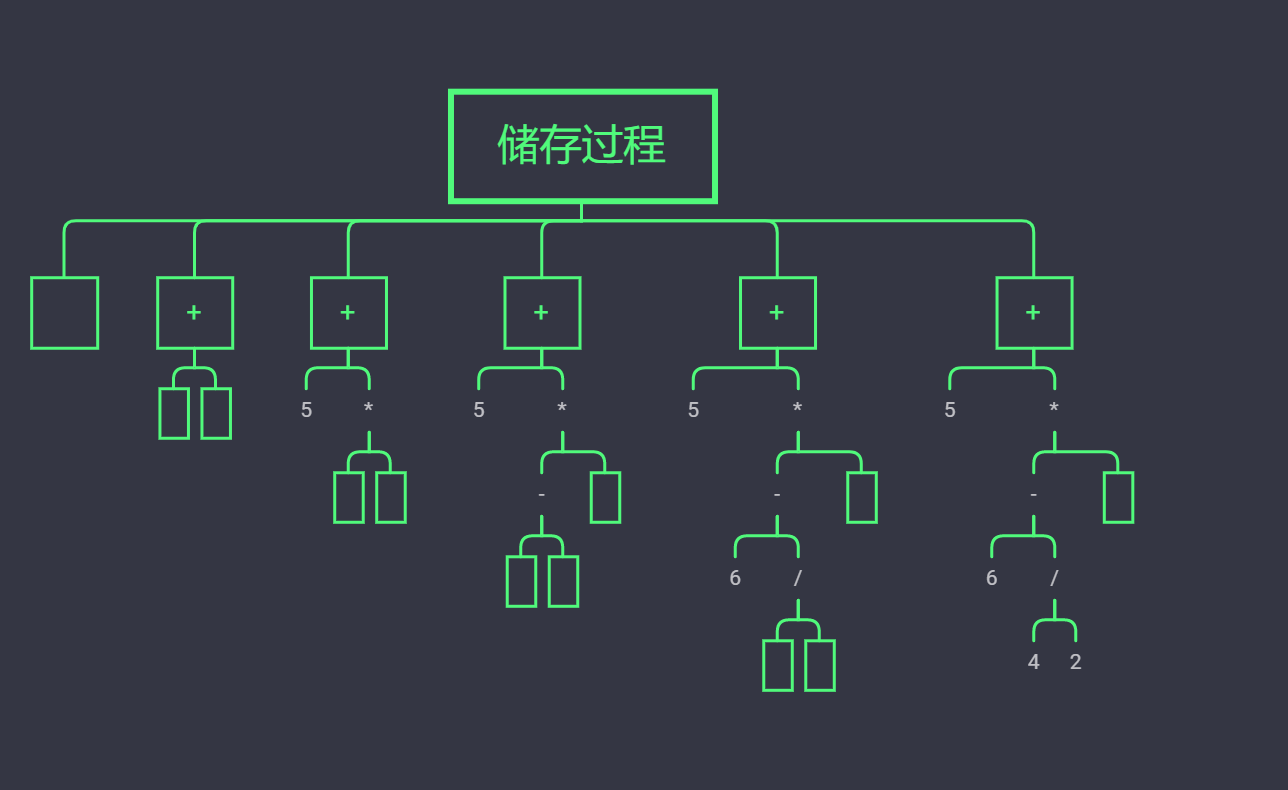
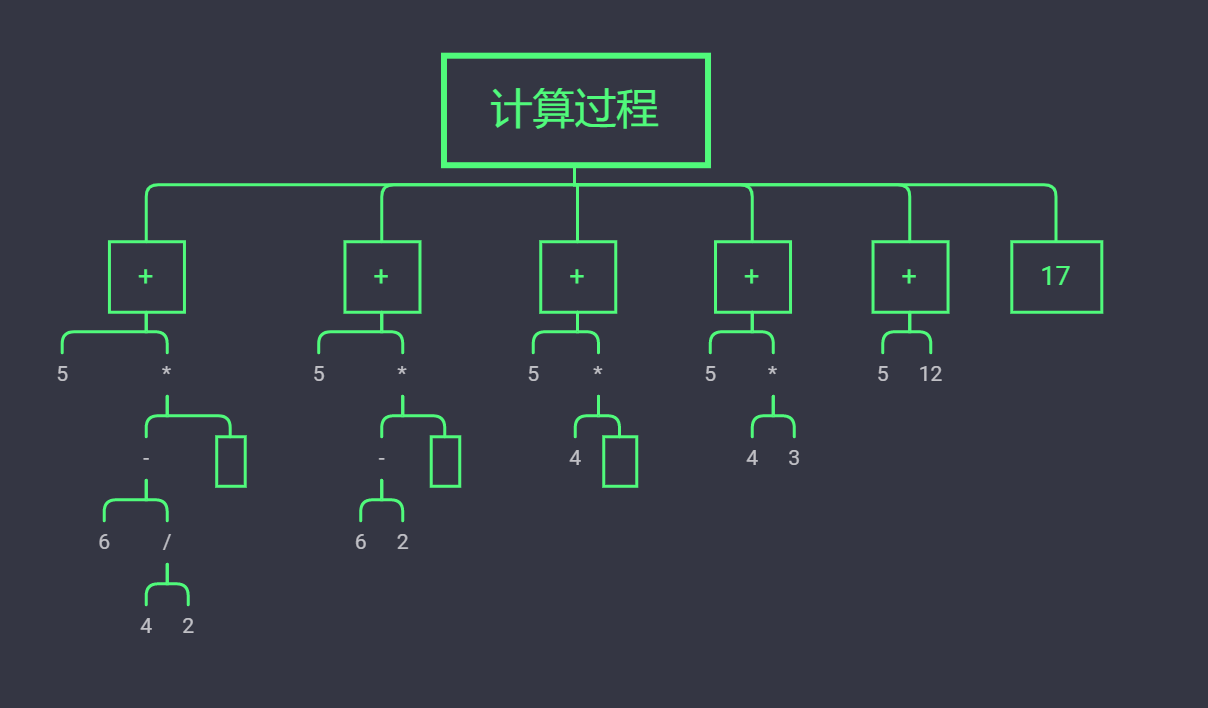
代码

#include<iostream>
#include<deque>

using namespace std;

double trans(deque<string> & a) {
    string s = a.front();
	a.pop_front();
	switch(s[0]) {
		case '+':
			return trans(a) + trans(a); //递归调用，求出自身包含的波兰式
		case '-':
			return trans(a) - trans(a);
		case '*':
			return trans(a) * trans(a);
		case '/':
			return trans(a) / trans(a);
		default:
			return atof(s.c_str()); //将char转换成对应的浮点数
			break;
	}
}

int main()
{
    int t;
    cin >> t;
    getchar();
    char c = getchar();
    for(int i = 0; i < t; i++)
    {
        deque<string>s;
        string str;
        cout << "case #" << i << ":"<<endl;
        while(c != 'n' && c != EOF)
        {
            if(c == ' ')
            {
                c = getchar();
                s.push_back(str);
                str = "";
                continue;
            }
            str += c;
            c = getchar();
        }

        s.push_back(str);
        str = "";

        // while(!s.empty())
        // {
        //     cout << s.back() << endl;
        //     s.pop_back();
        // }
        printf("%.6lfn",trans(s));
        c = getchar();
    }

    return 0;
}

最后

以上就是正直朋友为你收集整理的课后自主练习（递归）1057. 波兰表达式 easy《编程思维与实践》个人学习笔记的全部内容，希望文章能够帮你解决课后自主练习（递归）1057. 波兰表达式 easy《编程思维与实践》个人学习笔记所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。