数据结构–栈-C语言实现生成后缀表达式
前言
生成后缀表达式的代码是参考B站严蔚敏数据结构视频(版本很老),和现在《数据结构》上面的伪代码思路不一样。这里的算符(operator)仅仅涉及加、减、乘,除,另外”(“、”(“以及”#“作为分隔符(delimeter)也算作算符。算符是为了和操作数(operand)区分。
算符之间的优先关系参考《数据结构》这本书,上面定义的很详细。
本代码仅仅用了两个表达式检验程序,仅供参考,另外注释写得也很少,代码也未优化,请见谅。
运行环境:Dev-C++
思路


代码
/*
*预定义常量和类型
*00_state.h
*/
#ifndef __00_STATE_H__
#define __00_STATE_H__
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<time.h>
#include<windows.h>
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int Status;
#endif
/*
*02_stack_expression.h
*/
#include"00_state.h"
#define STACK_INIT_SIZE 100//存储空间初始分配量
#define STACK_INCREMENT 10//存储空间分配增量
typedef char StackElemType;
typedef struct{
StackElemType *base;
StackElemType *top;
int stacksize;//当前已经分配的存储空间
}stack;
Status stack_init(stack * pstack);//构造空栈
Status get_top(stack stack_,StackElemType *e);//获取栈顶元素
Status pop(stack *pstack,StackElemType *e);
Status stack_empty(stack stack_);
Status push(stack *pstack,StackElemType e);
/*
*02_stack_expression.cpp
*/
#include"02_stack_expression.h"
typedef enum Relationship{
GREATER,
LESS,
EQUAL,
NONE//没有关系
}Relate;
Relate rm[7][7] = {};
Status stack_init(stack * pstack)//构造空栈
{
pstack->base = (StackElemType*)malloc(STACK_INIT_SIZE*sizeof(StackElemType));
if(!pstack->base)
exit(OVERFLOW);
pstack->top = pstack->base;
pstack->stacksize = STACK_INIT_SIZE;
return OK;
}
Status get_top(stack stack_,StackElemType *e)//获取栈顶元素
{
if(stack_.top == stack_.base)
exit(1);
*e = *(stack_.top-1);
return TRUE;
}
Status push(stack *pstack,StackElemType e)
{
if(pstack->top-pstack->base>=pstack->stacksize)//指针相减
{
pstack->base = (StackElemType*)realloc(pstack->base,(pstack->stacksize+STACK_INCREMENT)*sizeof(StackElemType));
if(!pstack->base)
exit(OVERFLOW);
pstack->top=pstack->base+pstack->stacksize;
pstack->stacksize+=STACK_INCREMENT;
}
*(pstack->top) = e;//先赋值,然后指针上移
pstack->top++;
return OK;
}
Status pop(stack *pstack,StackElemType *e)
{
if(pstack->top==pstack->base)
{
printf("栈为空n");
return ERROR;
}
else
{
pstack->top--;//先指针下移,然后赋值
*e = *(pstack->top);
return OK;
}
}
Status stack_empty(stack stack_)
{
return stack_.base == stack_.top?TRUE:FALSE;
}
Status stack_trverse(stack stack_)
{
if(stack_.top == stack_.base)
{
printf("栈为空...n");
return ERROR;
}
else
{
StackElemType *p_trverse = stack_.base;
printf("栈元素遍历...n");
int i = 0;
while(p_trverse<stack_.top)
{
printf("元素%d:%cn",++i,*p_trverse++);
}
}
}
void print_rm(Relate rm[7][7])
{
//打印测试
int i = 0;
int j = 0;
for(;i<7;i++)
{
for(j = 0;j<7;j++)
{
switch(rm[i][j])
{
case GREATER:
printf(">t");
break;
case LESS:
printf("<t");
break;
case EQUAL:
printf("=t");
break;
case NONE:
printf("Nt");
break;
}
}
printf("n");
}
}
void get_ralationship_martrix(Relate rm[7][7])//relationship_martrix[][] 缩写rm[][]
{
//算符排列顺序:+,-,*,/,(,),#;
int i = 0;
int j=0;
while(j<2)
{
rm[i][j] = GREATER;
j++;
}
while(j<5)
{
rm[i][j] = LESS;
j++;
}
while(j<7)
{
rm[i][j] = GREATER;
j++;
}
//第二行
j = 0;
i = 1;
while(j<2)
{
rm[i][j] = GREATER;
j++;
}
while(j<5)
{
rm[i][j] = LESS;
j++;
}
while(j<7)
{
rm[i][j] = GREATER;
j++;
}
//第三行
j = 0;
i = 2;
while(j<4)
{
rm[i][j] = GREATER;
j++;
}
rm[i][j] = LESS;
j++;
while(j<7)
{
rm[i][j] = GREATER;
j++;
}
//第四行
j = 0;
i = 3;
while(j<4)
{
rm[i][j] = GREATER;
j++;
}
rm[i][j] = LESS;
j++;
while(j<7)
{
rm[i][j] = GREATER;
j++;
}
//第五行
j = 0;
i = 4;
while(j<5)
{
rm[i][j] = LESS;
j++;
}
rm[i][j] = EQUAL;
j++;
rm[i][j] = NONE;
//第六行
j = 0;
i = 5;
while(j<4)
{
rm[i][j] = GREATER;
j++;
}
rm[i][j] = NONE;
j++;
while(j<7)
{
rm[i][j] = GREATER;
j++;
}
//第七行
i = 6;
j = 0;
while(j<5)
{
rm[i][j] = LESS;
j++;
}
rm[i][j] = NONE;
j++;
rm[i][j] = EQUAL;
}
///
/*
*运算符仅包括加减乘除、小括号 、'#'
*分界符(delimeter)和操作符统称为算符
*/
Status in_operators(char ch)
{
switch(ch)
{
case '+':
break;
case '-':
break;
case '*':
break;
case '/':
break;
case '(':
break;
case ')':
break;
case '#':
break;
default:
return FALSE;
}
return TRUE;
}
Status precede(char pre_char,char post_char)//
{
char operatos[7] = {'+','-','*','/','(',')','#'};
int a = 0,b = 0;
for(int i = 0;i<7;i++)
{
if(pre_char ==operatos[i])
{
a = i;
break;
}
}
for(int i = 0;i<7;i++)
{
if(post_char ==operatos[i])
{
b = i;
break;
}
}
return rm[a][b]==GREATER?TRUE:FALSE;//
}
void generate_suffix_expression(char *source,stack *stack_expression)//重点
{
stack stack_;
stack_init(&stack_);//初始化一个栈用来存放操作符(OPERATOR)
push(&stack_,'#');
char *p_char_source = source;//用来遍历
char ch=*p_char_source;
while(!stack_empty(stack_))
{
if(!in_operators(ch))//符号不属于操作符,就作为操作数直接放到后缀表达式中
{
push(stack_expression,ch);
}
else//属于操作符
{
switch(ch)
{
case '(':
push(&stack_,ch);break;//左括号入栈
case ')':
char c1;
pop(&stack_,&c1);
while(c1!='(')//将括号里面的操作符号出栈传递给后缀表达式
{
push(stack_expression,c1);
pop(&stack_,&c1);
}
break;
default: //'#'或者加减乘除
char c2;
while(get_top(stack_,&c2)&&precede(c2,ch))//栈顶运算符高于新来的运算符
{
push(stack_expression,c2);
pop(&stack_,&c2);
}
if(ch!='#')
push(&stack_,ch);
else if(ch=='#'&&c2=='#')
{
pop(&stack_,&c2);
}
break;
}
}
if(ch!='#')//遍历
{
p_char_source++;
ch=*p_char_source;
}
}
stack_trverse(*stack_expression);
}
int main()
{
get_ralationship_martrix(rm);//relationship_martrix[][] 缩写rm[][]
char source[] = "a*b+(c-d/e)*f#";//"a*b+(c-d/e)*f#" -> "ab*cde/-f*+" ;"a*(b-c)#" ->"abc-*"
stack stack_expression;
stack_init(&stack_expression);
generate_suffix_expression(source,&stack_expression);
return 0;
}
结果
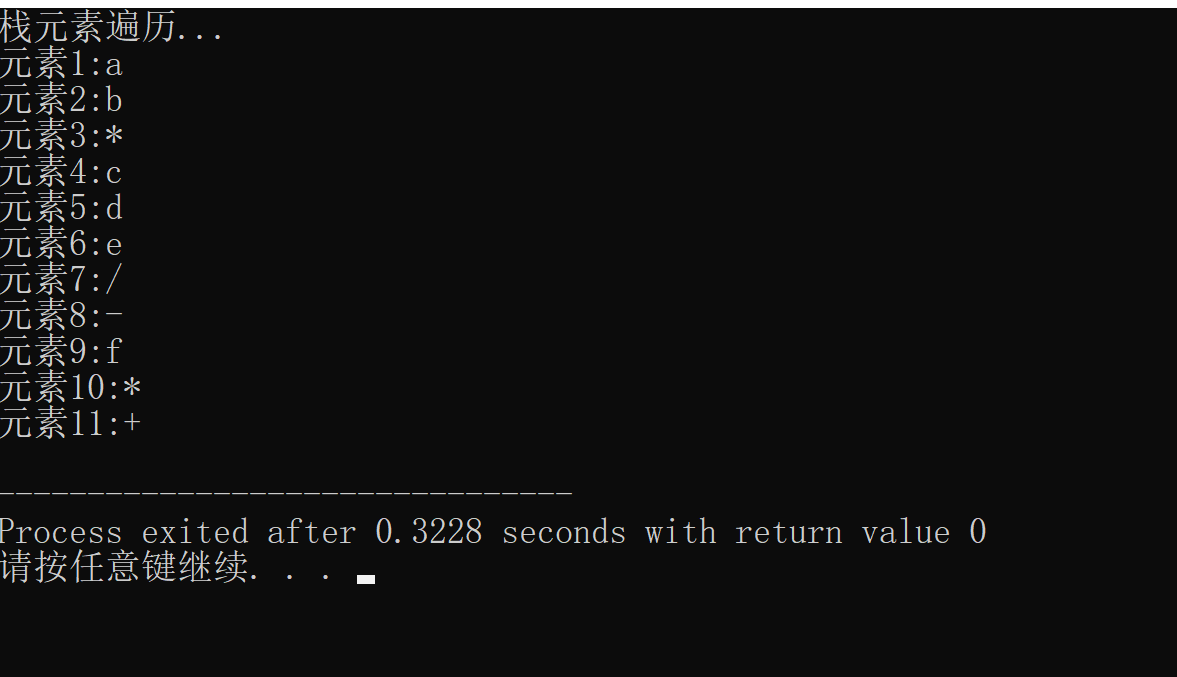
最后
以上就是美好缘分最近收集整理的关于数据结构--栈-C语言实现生成后缀表达式(没有计算表达式,仅仅生成)的全部内容,更多相关数据结构--栈-C语言实现生成后缀表达式(没有计算表达式内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复