文章目录
- `逆波兰表达式讲解`
- `正常表达式转换到逆波兰表达式`
- `栈操作逆波兰表达式的原理`
- 多位数压入栈操作
- `代码例题`
逆波兰表达式讲解
逆波兰表达式-----是数据结构的应用,你要单独说讨论它的话没有多大意义,如果我们结合数据结构中的栈来讲解的话,你将会对它有另一方面的认识。
让我们来看一下面表格:
| 正常表达式 | 逆波兰表达式 |
|---|---|
| (1+2)*(3-4) | 12+34-* |
但大家看到可能不会太懂,听我慢慢说:
左边这个正常表达式又叫做中缀表达式,什么是中缀表达式呢?简单来说就是把操作符放到操作数的中间。
右边这个叫做逆波兰表达式,又叫做后缀表达式,那什么又叫后缀表达式呢,和什么理解一样,后 顾名思义就是把操作符放到操作数后面。
带大家看看几个简单逆字波兰表达式的:
| 中缀表达式 | 逆波兰表达式 |
|---|---|
| (a+b) | ab+ |
| (a-b) | ab- |
| (a*b) | ab* |
目前我们只考虑这三种,除法的话计算机处理起来很麻烦,所以就先不考虑这个,我们主要是理解这种思想和栈的一种用法。
还有一点,我们将操作数压入栈时,是以字符形式压入的,你输入1,计算机会把它以字符 ‘1’ 的形式压入,除非你对它进行特殊操作。
正常表达式转换到逆波兰表达式
简单来说就是把操作符放到操作数后面,先看简单的:
a+b
1+2 —> 12+
ab
23 —> 23*
a-b
3-4 —> 34-
稍微复杂一点的:
(1+2)*(2 *5)
- (1+2)(2*5) *
- 12+(2*5) *
- 12+25**
(1+2)* (2*5) ---- > 12+25 * *
复杂一点的:
5*(((9+8)*(4 * 6))+7)
- 5(((9+8)* (4 * 6))+7)*
- 5((9+8)* (4 * 6))7+*
- 5(9+8)(4*6)*7+ *
- 598+46**7+*
5*(((9+8)* (4 * 6))+7)----> 598+46**7+*
栈操作逆波兰表达式的原理
一个这样逆波兰表达式:12+34-* —> 原型:(1+2)*(3-4)
计算机要利用栈操作来计算这个表达式的话,就要用到下面的原则:
-依次存入1和2,然后遇到操作符 ‘+’,就会把1 和 2 从栈里面取出来相加,然后把结果重新放到栈里面;
-再接着存入3 和 4,然后又遇到操作符 ‘-’ ,再把3和4取出来相加,结果存到栈里面;
-现在栈内已经有两个数了,接着存入,遇到 ‘ * ’,再把两个数取出来相乘,结果重新存到栈里,这样就可以得到整个表达式的结果了。看图解:
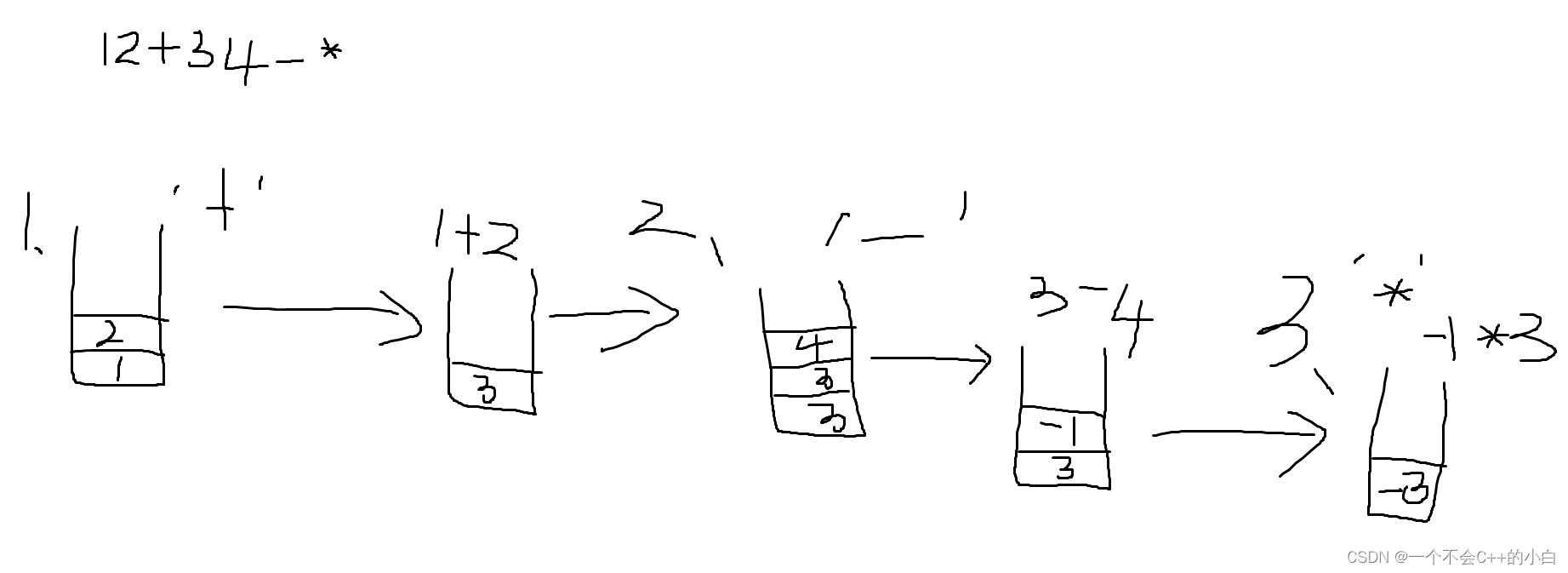
注: 栈是先入后出,后入先出,在做减法或除法时要把先入栈的数作为被减数或被除数(3-4)。
多位数压入栈操作
- 要将多位数压入栈的操作当然不能和个位数的一样,比如说将
30这个数压入栈的的话,就要做一些特殊的操作,具体如下:
string str;
while(st[i] >= '0' && st[i] <= '9')
{
str += st[i];//遇到第一个数字放到字符串中
while(st[i] >= '0' && st[i] <= '9')
{
str += st[i];//遇到第二个数字放到拼接到字符串中,就可以得到一个多位数了
}
push(stoi(str));//将多位数存入到栈里面
}
注:计算机存入的数字是字符,需要转换一下,一种方法是st[i] - '0' ;另一种是用一个函数stoi() , 这个函数是将用string定义的字符串转换为对应的数字。
代码例题
//这是栈应用的一个实例,逆波兰数
//(1+2)*(3-4)
//逆波兰表示法: (1+2)(3-4)*
// 12+34-*
//5*(((9+8)*(4*6))+7)
//逆波兰表示法:5((9+8)*(4*6))7+*
// 5(9+8)(4*6)*7+*
// 598+46**7+*
#include<iostream>
#include<cstring>
const int MAX = 512;
int top[MAX];//创建一个栈
int num = 0;
using namespace std;
bool is_full();//判断栈是否为满
bool is_temp();//判断栈是否为空
void push(int);//入栈操作
int pop();//出栈操作
int main()
{
char st[100];//存放逆波兰数,但存放的是字符
cout << "请输入逆波兰表达式:" << endl;
cin >> st;
int line = strlen(st);//计算出波兰数的长度
for(int i = 0; i < line; i++)
{//利用循环依次将字符存入到栈
str += st[i];
while(st[i] >= '0' && st[i] <= '9')
{
str += st[i];//遇到第二个数字放到拼接到字符串中,就可以得到一个多位数了
}
push(stoi(str));//将多位数存入到栈里面
}
else
{
int n = pop();//取出后入的两个数
int m = pop();
switch(st[i])
{
case '+'://遇到‘+’就将两个数相加
push(m + n);
break;
case '*':
push(m * n);//遇到‘*’就将两个数相加
break;
case '-':
push(m - n);//遇到‘-’就将两个数相加
break;
}
}
}
cout << "result: " << pop() << endl;//最后得出结果
return 0;
}
bool is_full()
{
return num == MAX;
}
bool is_temp()
{
return num == 0;
}
void push(int ch)
{
if(!is_full())
{
top[num++] = ch;
}
else
cout << "栈已满。" << endl;
}
int pop()
{
if(!is_temp())
{
return top[--num];
}
else
cout<< "栈已为空。" << endl;
}
最后
以上就是舒服雪糕最近收集整理的关于【数据结构】-------逆波兰表达式(C++)逆波兰表达式讲解正常表达式转换到逆波兰表达式栈操作逆波兰表达式的原理多位数压入栈操作代码例题的全部内容,更多相关【数据结构】-------逆波兰表达式(C++)逆波兰表达式讲解正常表达式转换到逆波兰表达式栈操作逆波兰表达式内容请搜索靠谱客的其他文章。








发表评论 取消回复