概述
无意间看到这样一道题：
private static final Integer END = Integer.MAX_VALUE;
private static final Integer START = END - 2;
public static void main(String[] args){
int count = 0;
for(int i = START ; i <= END ; i++ ){
count++;
}
}
请问这个for循环有没有问题？
托当下这么多毒鸡汤的福，一般情况下这样问别人，这情形绝对是有问题的，那么问题出在哪？
跑了一下代码发现，这是个死循环。。。。。。为毛一个确定的int类型最大值（这是一个常量啊）会导致死循环，换句话说，死循环意味着什么，意味着i赋值到int类型最大值之后，它会变成一个小一点的常量，然后继续自增1，直到加到最大值又变小–掉入死循环！！
上面都是猜想，正确不正确我们得用事实来说话，进入正题，在常规认知中，+1只会让数据变的更大，不可能 有10000+1变成0，但是，计算机语言中是有的，计算机中有些数据类型是带符号的（就是有正负 + —）就会出现一个最大数+了1变成了最小数（因为数据溢出了），下面我们来介绍一下计算机体系中基础中的基础—进制
As is known to all，计算机是用二进制计数法，为什么不是使用我们熟知的十进制呢？
在早期设计的常用的进制主要是十进制（因为我们有十个手指，所以十进制是比较合理的选择，用手指可以表示十个数字，0的概念直到很久以后才出现，所以是1－10而不是0－9）。电子计算机出现以后，使用电子管来表示十种状态过于复杂，所以所有的电子计算机中只有两种基本的状态，开和关。也就是说，电子管的两种状态决定了以电子管为基础的电子计算机采用二进制来表示数字和数据（反正都是这么说的）。
那么问题来了，为什么说用了二进制会让一个最大值+1就变成了最小值，这就又扯出了软件编程体系中的八大数据类型，不论是c还是Java，这基本的八大数据类型是一样的：
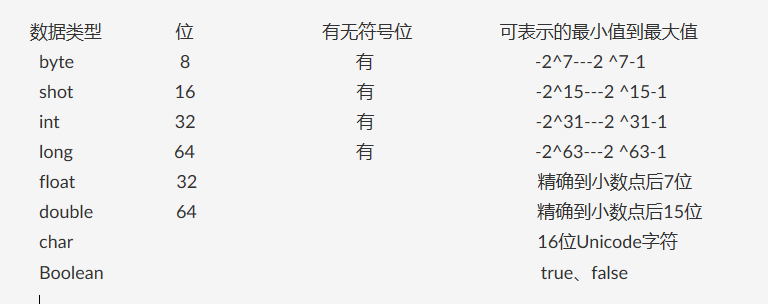
int ------Integer 这是装箱，反过来就是拆箱，有一篇文章讲拆箱和装箱挺好的（拆箱与装箱），在这里我们可以将它看成一回事（本篇主要说的是由溢出引发的死循环）
拿byte类型来说，是8位的二进制数据，前1位是符号位，后7位是数据真值（int类型的32位实在是太多了，就拿byte类型来举例子），首先说明一个概念，计算机是使用二进制的补码来存储汇编的机器码，这里边有三个知识点：原码、反码、补码
比如说，十进制的7，二进制是怎么个表示法？0111 1111，前1位是符号位，后7位是数据真值，说明什么？
（我就直接写上去）在符号位中 0代表正数，1代表负数，剩下的7位二进制码表示数值。
二进制转换十进制
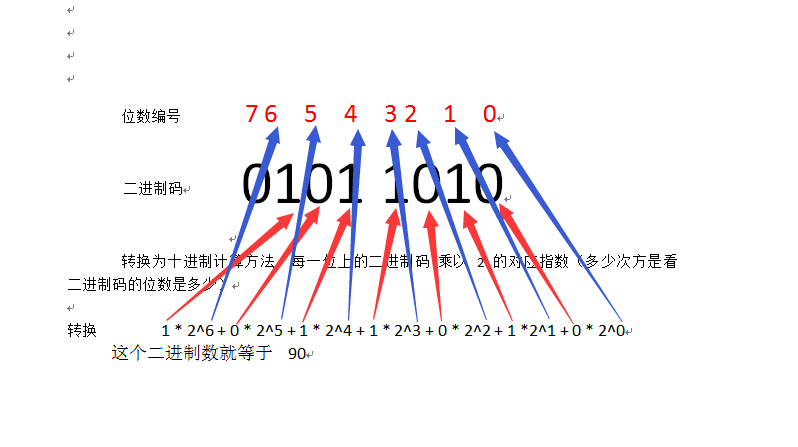
十进制 转换 二进制
这上面的二进制码呢，它叫原码，
注意一点，只有符号码才有原码反码补码！！！
- 原码
原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:
[+1]原 = 0000 0001
[-1]原 = 1000 0001
第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是:
[1111 1111 , 0111 1111]
即
[-127 , 127]
- 反码
反码的表示方法是:正数的反码是其本身,负数的反码是在其原码的基础上, 符号位不变，其余各个位取反.
[+1] = [00000001]原 = [00000001]反
[-1] = [10000001]原 = [11111110]反
可见如果一个反码表示的是负数, 人脑无法直观的看出来它的数值. 通常要将其转换成原码再计算.
- 补码
补码的表示方法是:正数的补码就是其本身
负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)
[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补
对于负数, 补码表示方式也是人脑无法直观看出其数值的. 通常也需要转换成原码在计算其数值.
总结一下就是：
- 正数的原码反码补码都是一样的
- 负数的反码，符号位不变，原码基础上按位取反；
- 负数的补码，符号位不变，反码基础上加1；
三. 为何要使用原码, 反码和补码
1.使用补码，可以将符号位和其它位统一处理；同时，减法也可按加法来处理。
2.使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数. 这就是为什么8位二进制, 使用原码或反码表示的范围为[-127, +127], 而使用补码表示的范围为[-128, 127]。
(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补
-1-127的结果应该是-128, 在用补码运算的结果中, [1000 0000]补 就是-128. 但是注意因为实际上是使用以前的-0的补码来表示-128, 所以-128并没有原码和反码表示.(对-128的补码表示[1000 0000]补算出来的原码是[0000 0000]原, 这是不正确的)
现在来回答最初的那个问题：
private static final Integer END = Integer.MAX_VALUE;
private static final Integer START = END - 2;
public static void main(String[] args){
int count = 0;
for(int i = START ; i <= END ; i++ ){
count++;
}
}
我们依然假设这个int类型 是byte，原因和上面是一样的，那么 最大值 END = 127 ， 起始值START = 125 ，起初呢 ，for循环是正常的，当它走到 i = 127 127<=127 所以它还是会走近这个循环，当循环要完毕的时候，i + 1 = 128（逻辑上来说是这样），我们来看看 byte类型的 127 +1 是个什么玩意？
127的原码：0111 1111
127的反码：0111 1111
127的补码：0111 1111
1的原码：0000 0001
1的反码：0000 0001
1的补码：0000 0001
计算机都是使用补码存储的
127的补码：0111 1111
+
1的补码： 0000 0001
= 1000 0000，这在二进制里表示-128 ，所以结论就是当Integer.MAX_VALUE+1之后，它会等于 Integer的最小值，导致，这个for循环变成了一个死循环。
其余的原码反码补码可以在这个资料里去学习：https://www.cnblogs.com/maoypeng/archive/2018/06/01/9123826.html
今天看到别人代码中写了 &=（与） |=（或） ^=（非）这样的位运算符，之前也复习了一下，但是过了一个月就给忘记了，还是记录成笔记靠谱。下面来解释这几个位运算符的涵义：对了，还有一个基础就是不论是数学逻辑也好，计算机程序中也好，0 代表为真（true），1代表为假（false）
①：&= 二进制位与运算，a&=b 其实和a+=b是一样的，a&=b ==> a = a & b ，就是正常的先做 & 操作，再赋值给a，我们一直强调计算机是用二进制来做运算的，这里也是一样，那么 在二进制运算中，&运算是怎么做？
记得高中学这一段的时候有一个口诀，叫同真为真，我们来把这个 a&=b换成具体的数字好解释，int a= 8&=16 看看这里的a等于多少，也就是说 先做位运算与 --8&16，然后将结果赋值给a，
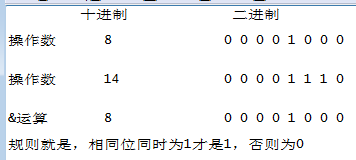
②：|= 二进制位或运算，a|=b 这就和上面的计算方法没什么区别了，只是高中数学的口诀变成 遇真为真
③：^= 二进制位非运算，a ^=b 相同位结果为"异"，结果为false（1），否则是true（0）
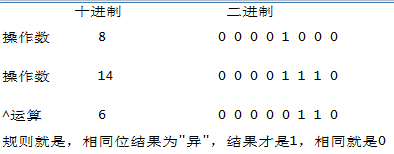
这是复数类型的计算机体系数字运算，如果是布尔值，直接套用上面的口诀就能得出正确结果
最后
以上就是快乐月饼为你收集整理的由一道二进制溢出题引发的进制_原码反码补码回顾（操作系统原理）的全部内容，希望文章能够帮你解决由一道二进制溢出题引发的进制_原码反码补码回顾（操作系统原理）所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复