Leetcode 加油站②

即如果某个位置开始，不断的累加往下走，当某个位置走不通时，最开始那个点前移（退回补油）
直到能够完整走一圈：此时相遇点即为 ：一个可行的出发点。

题目描述
N个加油站组成一个环形，给定两个长度都是N的非负数组oil和dis(N>1)，oil[i]代表第i个加油站存的油可以跑多少千米，dis[i]代表第i个加油站到环中下一个加油站相隔多少千米。假设你有一辆油箱足够大的车，初始时车里没有油。如果车从第i个加油站出发，最终可以回到这个加油站，那么第i个加油站就算良好出发点，否则就不算。请返回长度为N的boolean型数组res，res[i]代表第i个加油站是不是良好出发点
规定只能按照顺时针走，也就是i只能走到i+1，N只能走到1
[要求]
时间复杂度为O(n)

问题思路

首先根据回退的思想，找到一个可行的出发点（若没有，那么所有点都不是良好出发点）
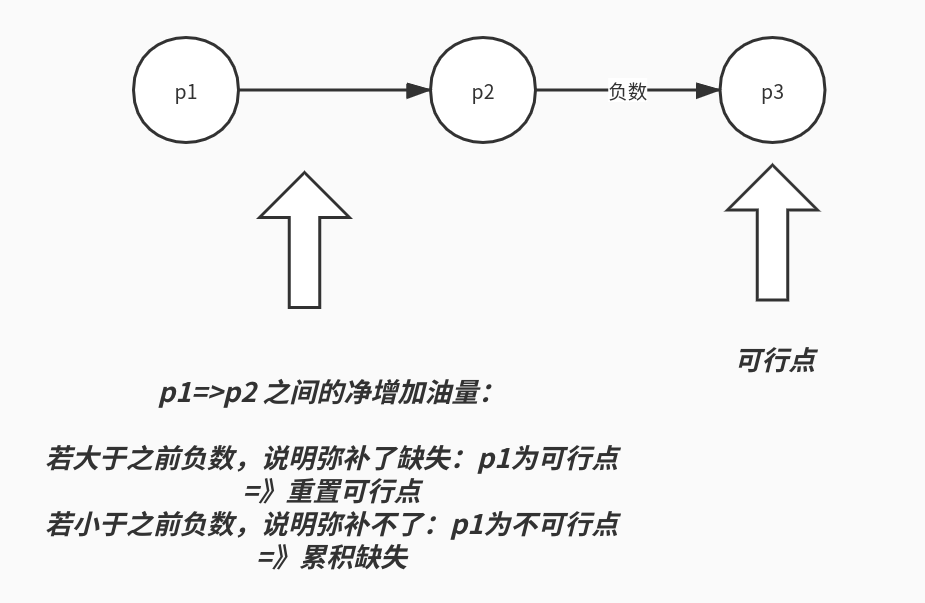
然后，研究可行点之前的点，是否可行，其基本策略为：
如果ret>=0 其表示能够走到下一个可行点 ans[i]=1 同时ret设置为 ret=oil[start-1]-cost[start-1]
如果ret<0 其表示不能走到下一个可行点 ans[i]=0 同时 ret+=oil[start-1]-cost[start-1]
其含义为：更前面的点必须弥补上这些代价。

代码实现

#include<iostream>
#include<vector>
using namespace std;
int main()
{
    long n;
    cin>>n;
    vector<long> oil(n);
    vector<long> dis(n);
    vector<int> can(n,-1);
    for(int i=0;i<n;i++)
        cin>>oil[i];
    for(int j=0;j<n;j++)
    {
          cin>>dis[j];
           oil[j]-=dis[j];
        
    }
    //那么oil[i]=k  表示单独走第i部分 剩余油量为k
    
    
    long start=n-1;
    long end=0;
    long sum=oil[start];
    while(end<start)  //没有相遇
    {
        if(sum>0)  //油量充足
        {
            sum+=oil[end];
            end=(end+1)%n;   
        }
        else
        {
            start=(start-1+n)%n;
            sum+=oil[start];
        }  
    }
    if(sum>0)  //说明从start点出发可以走一圈
    {
        
       
        long ret=oil[start]; 
        while(can[start]==-1)  //循环跳出的条件是 一圈结束
        {
            if(ret>=0)
            {
                can[start]=1;
                start=(start-1+n)%n;
                ret=oil[start];   //重置比较的可行点
            }
            else
            {
                can[start]=0;
                start=(start-1+n)%n;
                ret+=oil[start];   //可能需要累积上代价
            } 
           
        }
 
    }
    else
    {
        for(int i=0;i<n;i++)
            can[i]=0;  ///没有任何一个可行点
    }

    for(auto i:can)
        cout<<i<<" ";
    
    
}

最后

以上就是含糊电脑为你收集整理的Leetcode 加油站②的全部内容，希望文章能够帮你解决Leetcode 加油站②所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。