函数的抽样与复原

78 阅读 0 评论 52 点赞

我是靠谱客的博主无情香烟，最近开发中收集的这篇文章主要介绍函数的抽样与复原，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

本文为对钱晓凡老师编著的《信息光学数字实验室》代码内容复现的一些思考整理。更多理论详细内容，请查阅相关书籍。
实验内容

（1）利用Matalb中自带的peaks函数创建一个二维带限函数，通过傅里叶变换观察其频谱，并测量其带宽，理解“带限”的含义；
（2）构建二维梳状函数，并显示其空间分布及频谱，观察改变梳状函数的空间间隔——抽样间隔后频谱的变化；
（3）利用梳状函数对连续函数抽样，得到该函数的抽样函数，在空域观察抽样函数；
（4）观察抽样函数的频谱，并与原连续函数的频谱做比较，体会抽样函数的频谱、梳状函数的频谱，以及连续函数的频谱之间的卷积关系；
（5）改变抽样间隔，或调整原连续函数的带宽，观察抽样函数频谱的混叠和分离现象，总结其规律；
（6）根据抽样间隔构建二维矩形函数滤波器，并对抽样函数的频谱完成滤波和逆傅里叶变换，观察原连续函数的带宽改变，或抽样间隔改变后，利用抽样函数重构原函数的效果，体会欠采样，继而理解抽样定理。

1 构建一个带限函数并显示

%% (1) 带限函数
fxy=cos(peaks(256).*2+pi)+1;  %构建连续带限函数,只在频率空间的有限区域R上不为0
[rr,cc]=size(fxy);                       %计算连续函数的大小
figure,imshow(fxy,[])                   %显示连续函数
F=fftshift(fft2(fxy));                  %计算连续函数的频谱
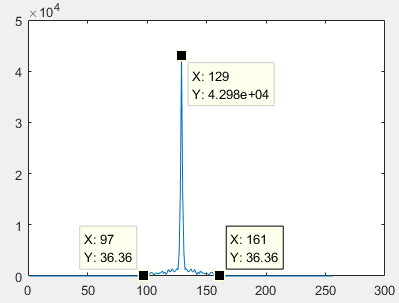
figure,plot(abs(F(round(rr/2)+1,:))),   %观察带宽  行 x方向
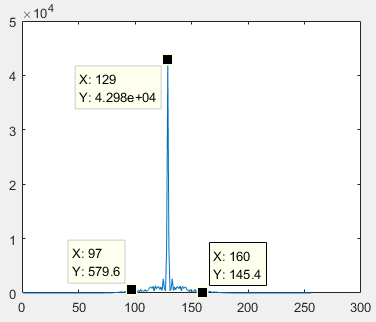
figure,plot(abs(F(:,round(cc/2)+1))),   %观察带宽 列 y方向
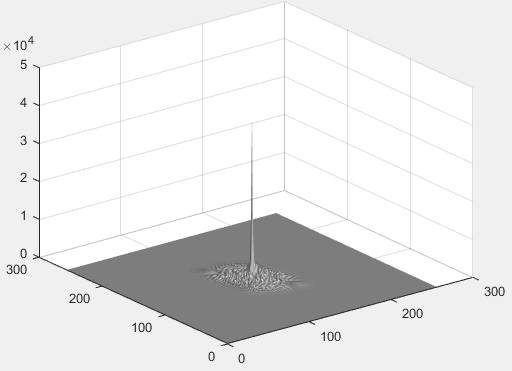
figure,surfl(abs(F)),shading interp,colormap(gray);   %频谱3D图

原函数图像
在这里插入图片描述
x方向频谱

y方向频谱

频谱三维显示

2 构建一个梳状采样函数并显示

combxy=zeros(rr,cc);                    %开始生成comb函数
X=4;Y=4;                                %抽样间隔
for n=1:Y:rr
   for m=1:X:cc
   combxy(n,m)=1;
   end
end
figure,imshow(combxy,[]);               %显示comb函数
% figure,mesh(combxy)
C=fftshift(fft2(combxy));               %计算comb函数的频谱
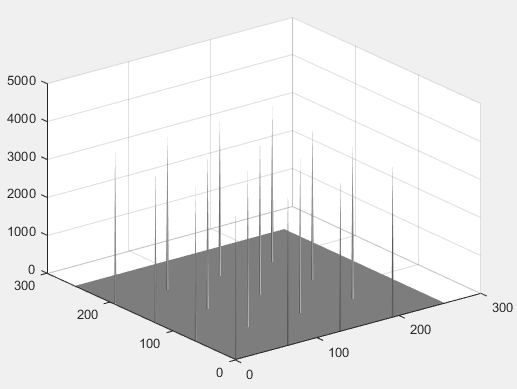
figure,surfl(abs(C)),shading interp,colormap(gray); % 频谱3D图，间隔256/X

二维梳状函数
在这里插入图片描述
x,y方向是均隔4个点取一个值。
梳状函数频谱显示（因原始图像大小为256×256个像素，傅里叶变换后（对称）最高空间频率为 $256/2=128m^{-1}$ ）,梳状函数频率间隔为256/4=64

3 用构建的梳状函数对原函数进行采样

%% (3) 梳状函数抽样
gxy=zeros(rr,cc);                         %定义抽样函数
gxy=fxy.*combxy;                        %生成抽样函数
figure,imshow(gxy,[]);                  %显示抽样函数```

**采样后函数显示**
![在这里插入图片描述](https://img-blog.csdnimg.cn/20210415172109290.png)
## 4 观察抽样后函数的频谱

```c
%% （4）抽样函数频谱
Gs=fftshift(fft2(gxy));                 %计算抽样函数的频率
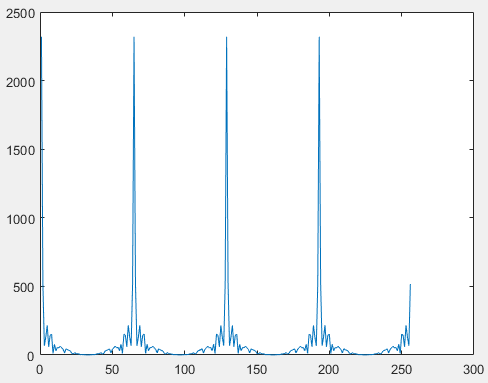
figure,surfl(abs(Gs)),shading interp,colormap(gray); %频谱3D图
figure,plot(abs(Gs(:,cc/2+1))),         %观察频谱是否有重叠

观察抽样后的函数频谱
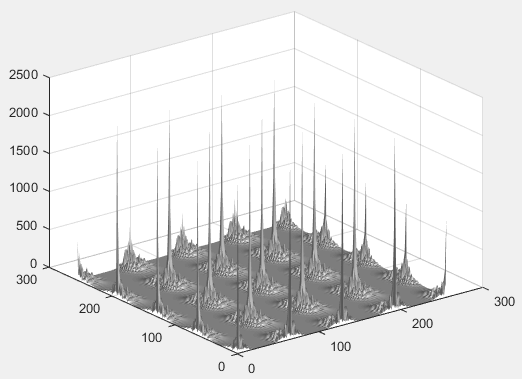
在这里插入图片描述
观察某一列频谱y方向

在这里插入图片描述

4 滤波并恢复函数

从上述观察到的频谱可以看出，要想从抽样后的函数中恢复原函数，滤波函数窗宽 $g_x = 64, g_y = 64$
将中心频谱截出。

%% （6）滤波器
By=round(rr/2/Y);
Bx=round(cc/2/X);      %二维矩函数滤波器的宽度
H=zeros(rr,cc);                         %开始生成二维矩函数滤波器
H(round(rr/2)+1-By:round(rr/2)+1+By-1,round(cc/2)+1-Bx:round(cc/2)+1+Bx-1)=1;  
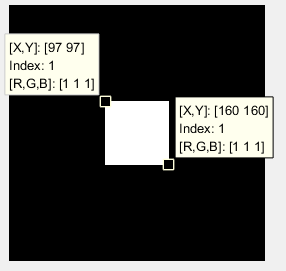
figure,imshow(H,[])                     %显示二维矩函数滤波器
Gsyp=H.*Gs;                             %滤波计算原函数频谱
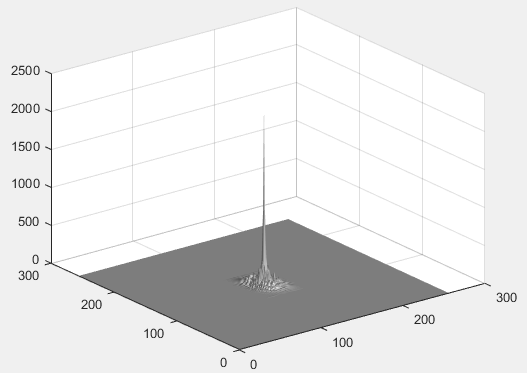
figure,surfl(abs(Gsyp)),shading interp,colormap(gray);

gxyyp=X*Y.*abs(ifft2(fftshift(Gsyp)));            %逆傅里叶变换计算原函数
figure,imshow(gxyyp,[])                 %显示还原的原函数

diff = fxy - gxyyp;        %%原函数与还原后的函数差值
figure,imshow(diff,[])    %%显示差值

显示二维滤波器
在这里插入图片描述
滤出后频谱

显示还原后的函数

空域抽样间隔分别为X和Y，则离散信号的幅度应该是原函数频谱的 $1 / (X Y)$ ，为保证幅度正确，必须让用FFT计算得到的结果乘以XY。
显示原函数与还原后函数的差值
在这里插入图片描述

5 思考

1、原函数带宽提高，变为原来的2倍

fxy=cos(peaks(256).*4+pi)+1;  %构建连续带限函数,只在频率空间的有限区域R上不为0

若依然采用原来的抽样间隔X=Y=4，重复之前的结果，可以看到最后复原后的结果为：
在这里插入图片描述
在蓝色先圈出区域，均未能完整恢复原函数特征。
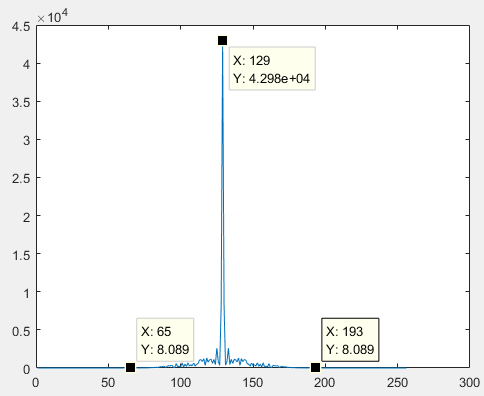
究其原因为，原函数频率提升，我们先来看看它的带宽，这里取方向进行展示，x方向带宽依旧为64个像素。可以看到y方向的带宽 $2B_y=128^{-1}m$ ，根据抽样定理，要能够重构原函数的条件是抽样间隔至少满足Y=256*2B_y=2个像素。上述实验中，仍取X=Y=4个像素，不满足抽样定理，故发生了欠采样。
在这里插入图片描述
抽样间隔变为X=4，Y=2后，复原结果为。