径向基函数分类

大多数情况下，利用二维控件线性是无法分类的，这个时候就需要将维度提高，在更高阶的维度进行分类，径向基函数是变换到高纬度的方法之一。目前，最常用的径向基函数是高斯核函数，其公式如下：

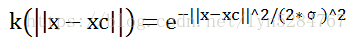
其中，xc为中心点坐标，x为待分类的坐标，||x-xc||为欧几里得距离,σ为可调的宽度参数。

python代码：

#径向基函数，gamma=1/(2*σ)^2

def rbf(v1,v2,gamma=10):
  dv=[v1[i]-v2[i] for i in range(len(v1))]
  l=veclength(dv)
  return math.e**(-gamma*l)

#计算||x-xc||^2
def veclength(v):
  return sum([p**2 for p in v])

#计算偏移量
def getoffset(rows, gamma=10):
    l0 = []
    l1 = []
    for row in rows:
        if row.match == 0:
            l0.append(row.data)
        else:
            l1.append(row.data)
    sum0 = sum(sum([rbf(v1, v2, gamma) for v1 in l0]) for v2 in l0)
    sum1 = sum(sum([rbf(v1, v2, gamma) for v1 in l1]) for v2 in l1)

    return (1.0 / (len(l1) ** 2)) * sum1 - (1.0 / (len(l0) ** 2)) * sum0

#分类，计算输入点到每个类中各个点的径向基函数，取均值。离count0近则返回0，离count1近则返回1
def nlclassify(point, rows, offset, gamma=10):
    sum0 = 0.0
    sum1 = 0.0
    count0 = 0
    count1 = 0

    for row in rows:
        if row.match == 0:
            sum0 += rbf(point, row.data, gamma)
            count0 += 1
        else:
            sum1 += rbf(point, row.data, gamma)
            count1 += 1
    y = (1.0 / count0) * sum0 - (1.0 / count1) * sum1 + offset

    if y > 0:
        return 0
    else:
        return 1

最后

以上就是神勇黄蜂为你收集整理的径向基函数分类的全部内容，希望文章能够帮你解决径向基函数分类所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。