数据分析与挖掘实战-应用系统负载分析与磁盘容量预测应用系统负载分析与磁盘容量预测

75 阅读 0 评论 50 点赞

我是靠谱客的博主冷静斑马，最近开发中收集的这篇文章主要介绍数据分析与挖掘实战-应用系统负载分析与磁盘容量预测应用系统负载分析与磁盘容量预测，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

应用系统负载分析与磁盘容量预测

背景
- 某大型企业为了信息化发展的需要，建设了办公自动化系统、人力资源管理系统、财务管理系统、企业信息门户系统等几大企业级应用系统。因应用系统在日常运行时，会对底层软硬件造成负荷，显著影响应用系统性能。
- 一般认为，影响应用系统性能的因素包括：服务器、数据库、中间件和存储设备。任何一种资源负载过大，都可能会引起应用系统性能下降甚至瘫痪。因此，需要关注服务器、数据库、中间件和存储设备的运行状态，及时了解当前应用系统的负载情况，以便提前预防，确保系统安全稳定运行。
目标
- 应用系统的负载率可以通过对一段时间内软硬件性能的运行情况进行综合评分而获得。通过对系统的当前负载率与历史平均负载率进行比较，获得负载率的当前趋势。通过负载率以及负载趋势可对系统进行负载分析。当出现应用系统的负载高或者负载趋势大的情况，代表系统目前处于高危工作环境中。如果系统管理员不及时进行相应的处理，系统很容易出现故障，从而导致用户无法访问系统，严重影响企业的利益。
- 本案例重点分析存储设备中磁盘容量预测，通过对磁盘容量进行预测，可以预测磁盘未来的负载情况，避免应用系统因出现存储容量耗尽的情况而导致应用系统负载率过高，最终引发系统故障。
- 目前监控采集的性能数据主要包含CPU使用信息、内存使用信息和磁盘使用信息等。通过分析磁盘容量相关数据，预测应用系统服务器磁盘空间是否满足系统健康运行的要求。实现以下目标。
  - 针对历史磁盘数据，采用时间序列分析方法，预测应用系统服务器磁盘已使用空间大小。
  - 根据用户需求设置不同的预警等级，将预测值与容量值进行比较，对其结果进行预警判断，为系统管理员提供定制化的预警提示。
分析
- 应用系统出现故障通常不是突然瘫痪造成的(除非服务器断电），而是一个渐变的过程。例如，系统长时间运行，数据会持续写入存储，存储空间逐渐变少，最终磁盘被写满而导致系统故障。由此可知，在不考虑人为因素的影响时，存储空间随时间变化存在很强的关联性，且历史数据对未来的发展存在一定的影响，所以本案例可采用时间序列分析法对磁盘已使用空间进行预测分析。
- 流程如下
  - 从数据源中选择性抽取历史数据与每天定时抽取数据。
  - 对抽取的数据进行周期性分析以及数据清洗、数据变换等操作后，形成建模数据。
  - 采用时间序列分析法对建模数据进行模型构建，利用模型预测服务器磁盘已使用情况。
  - 应用模型预测服务器磁盘将要使用情况，通过预测到的磁盘使用大小与磁盘容量大小按照定制化标准进行判断，将结果反馈给系统管理员，提示管理员需要注意磁盘的使用情况。

处理过程

数据获取
- 磁盘使用情况的数据都存放在性能数据中，而监控采集的性能数据中存在大量的其他属性数据。为了抽取出磁盘数据，以属性的标识号（TARGET_ID）与采集指标的时间（COLLECTTIME）为条件，对性能数据进行抽取。本案例抽取2014-10-01到2014-11-16财务管理系统中某一台数据库服务器的磁盘相关数据。
数据探索
- 由于本案例使用时序分析法进行建模，为了建模需要，需要探索数据的平稳性。通过时序图可以初步发现数据的平稳性。针对磁盘已使用大小，以天为单位进行周期性分析。
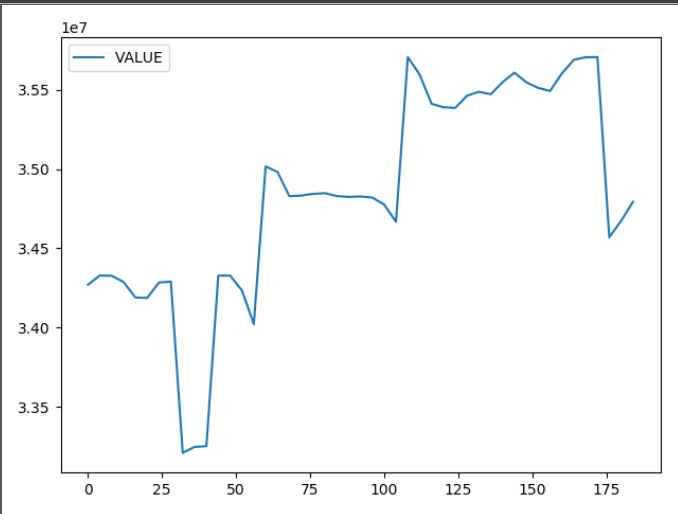
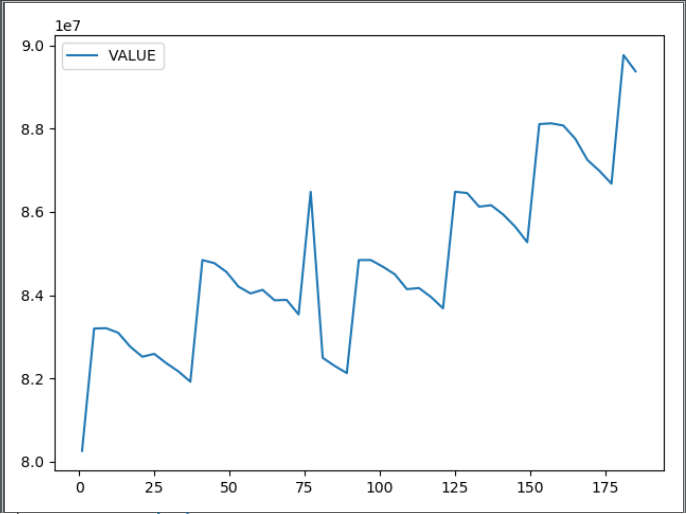
- 由上图，不难看出磁盘的使用情况不具有周期性，它们表现出缓慢增长，呈现趋势性。因此，初步确认数据是非平稳的。
- 代码见GitHub
数据预处理
- 数据清洗
  - 实际的业务中，监控系统会每天定时对磁盘的信息进行收集，但是一般情况下，磁盘的容量属性都是一个定值，因此磁盘原始数据中会存在磁盘容量的重复数据。在数据清洗的过程中，剔除磁盘容量的重复数据，并且将所有服务器的磁盘容量作为一个固定值，方便模型预警。
- 属性构造
  - 由于每台服务器的磁盘信息可以通过NAME、TARGET_ID、ENTITY三个属性进行区分，且每台服务器的上述三个属性是不变的，可以进行合并。
  - 代码见GitHub

数据挖掘建模

数据集划分
- 最后5条记录作为验证数据，其余作为建模样本数据。
容量预测模型
- 流程
  - 首先需要对观测值序列进行平稳性检验，如果不平稳，则对其进行差分处理直到差分后的数据平稳。在数据平稳后，对其进行白噪声检验。如果没有通过白噪声检验，就进行模型识别，识别其模型属于AR、MA和ARMA中的哪一种模型。并且通过BIC信息准则对模型进行定阶，确定ARIMA模型的p，q参数。在模型识别后需进行模型检验，检验模型残差序列是否为白噪声序列。如果模型没有通过检测，需要对其进行重新识别。对已通过检验的模型采用极大似然估计方法进行模型参数估计。最后，应用模型进行预测，将实际值与预测值进行误差分析。如果误差较小（误差阈值通过业务分析进行设定），表明模型拟合效果较好，则模型可以结束。反之需要重新估计参数。
- 平稳性检验
  - 为了确定原始数据序列中没有随机趋势或确定趋势，需要对数据进行平稳性检验，否则将会产生“伪回归”现象。本案例采用单位根检验（ADF）的方法或者时序图的方法进行平稳性检验。
- 白噪声检验
  - 为了验证序列中有用的信息是否已被提取完毕，需要对噪声进行白噪声检验。如果序列检验为白噪声序列，就说明序列中的有用信息已被提取完毕，剩下的全是随机扰动，无法进行预测和使用。本案例使用LB统计量的方法进行白噪声检验。
- 模型识别
  - 采用极大似然比方法进行模型的参数估计，估计各个参数的值。然后针对各个不同模型，采用BIC信息准则对模型进行定阶，确定p，q参数，从而选择最优模型。
- 模型检验
  - 模型确定后，检验其残差序列是否为白噪声。如果不是白噪声，说明残差中还存在有用的信息，需要修改模型或者进一步提取。本案例所确定的ARIMA（0,1,1）模型成功通过检验。
- 模型预测
  - 应用通过检测的模型进行预测，获取未来5天的预测值，并且与实际值作比较，也就是建模忽略的最后5个数据。
模型评价
- 为了评价时序预测模型效果的好坏，本案例采用3个衡量模型预测精度的统计量指标：平均绝对误差、均方根误差和平均绝对百分误差。结合业务分析，误差阈值设定为1.5。

代码如下

  # -*- coding:utf-8 -*-
  import pandas as pd
  
  
  
  def stationarityTest():
      '''
      平稳性检验
      :return:
      '''
      discfile = 'data/discdata_processed.xls'
      predictnum = 5
  
      data = pd.read_excel(discfile)
      data = data.iloc[: len(data) - predictnum]
      # 平稳性检验
      from statsmodels.tsa.stattools import adfuller as ADF
      diff = 0
      adf = ADF(data['CWXT_DB:184:D:\'])
      while adf[1] > 0.05:
          diff = diff + 1
          adf = ADF(data['CWXT_DB:184:D:\'].diff(diff).dropna())
  
      print(u'原始序列经过%s阶差分后归于平稳，p值为%s' % (diff, adf[1]))
  
  
  def whitenoiseTest():
      '''
      白噪声检验
      :return:
      '''
      discfile = 'data/discdata_processed.xls'
      data = pd.read_excel(discfile)
      data = data.iloc[: len(data) - 5]
      # 白噪声检验
      from statsmodels.stats.diagnostic import acorr_ljungbox
      [[lb], [p]] = acorr_ljungbox(data['CWXT_DB:184:D:\'], lags=1)
      if p < 0.05:
          print(u'原始序列为非白噪声序列，对应的p值为：%s' % p)
      else:
          print(u'原始该序列为白噪声序列，对应的p值为：%s' % p)
      [[lb], [p]] = acorr_ljungbox(data['CWXT_DB:184:D:\'].diff().dropna(), lags=1)
      if p < 0.05:
          print(u'一阶差分序列为非白噪声序列，对应的p值为：%s' % p)
      else:
          print(u'一阶差分该序列为白噪声序列，对应的p值为：%s' % p)
  
  
  def findOptimalpq():
      '''
      得到模型参数
      :return:
      '''
      discfile = 'data/discdata_processed.xls'
      data = pd.read_excel(discfile, index_col='COLLECTTIME')
      data = data.iloc[: len(data) - 5]
      xdata = data['CWXT_DB:184:D:\']
  
      from statsmodels.tsa.arima_model import ARIMA
  
      # 定阶
      # 一般阶数不超过length/10
      pmax = int(len(xdata) / 10)
      qmax = int(len(xdata) / 10)
      # bic矩阵
      bic_matrix = []
      for p in range(pmax + 1):
          tmp = []
          for q in range(qmax + 1):
              try:
                  tmp.append(ARIMA(xdata, (p, 1, q)).fit().bic)
              except:
                  tmp.append(None)
          bic_matrix.append(tmp)
  
      bic_matrix = pd.DataFrame(bic_matrix)
      # 先用stack展平，然后用idxmin找出最小值位置。
      p, q = bic_matrix.stack().astype('float64').idxmin()
      print(u'BIC最小的p值和q值为：%s、%s' % (p, q))
  
  
  def arimaModelCheck():
      '''
      模型检验
      :return:
      '''
      discfile = 'data/discdata_processed.xls'
      # 残差延迟个数
      lagnum = 12
  
      data = pd.read_excel(discfile, index_col='COLLECTTIME')
      data = data.iloc[: len(data) - 5]
      xdata = data['CWXT_DB:184:D:\']
      # 建立ARIMA(0,1,1)模型
      from statsmodels.tsa.arima_model import ARIMA
      # 建立并训练模型
      arima = ARIMA(xdata, (0, 1, 1)).fit()
      # 预测
      xdata_pred = arima.predict(typ='levels')
      # 计算残差
      pred_error = (xdata_pred - xdata).dropna()
  
      from statsmodels.stats.diagnostic import acorr_ljungbox
      # 白噪声检验
      lb, p = acorr_ljungbox(pred_error, lags=lagnum)
      # p值小于0.05，认为是非白噪声。
      h = (p < 0.05).sum()
      if h > 0:
          print(u'模型ARIMA(0,1,1)不符合白噪声检验')
      else:
          print(u'模型ARIMA(0,1,1)符合白噪声检验')
  
  
  def calErrors():
      '''
      误差计算
      :return:
      '''
      # 参数初始化
      file = 'data/predictdata.xls'
      data = pd.read_excel(file)
  
      # 计算误差
      abs_ = (data[u'预测值'] - data[u'实际值']).abs()
      mae_ = abs_.mean()  # mae
      rmse_ = ((abs_ ** 2).mean()) ** 0.5
      mape_ = (abs_ / data[u'实际值']).mean()
  
      print(u'平均绝对误差为：%0.4f，n均方根误差为：%0.4f，n平均绝对百分误差为：%0.6f。' % (mae_, rmse_, mape_))
  
  
  if __name__ == '__main__':
      # stationarityTest()
      # whitenoiseTest()
      # findOptimalpq()
      arimaModelCheck()
      calErrors()