BatchNorm2d那些事儿为什么需要Batchnorm数据准备训练时测试参考结语

62 阅读 0 评论 41 点赞

我是靠谱客的博主文艺百褶裙，最近开发中收集的这篇文章主要介绍BatchNorm2d那些事儿为什么需要Batchnorm数据准备训练时测试参考结语，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

为什么需要Batchnorm

下面举出一个简单的例子：就比如说Sigmoid函数的函数值域在 [0,1] 之间，但是如果我们对sigmoid函数求导之后我们发现其为： sigmoid′=sigmoid(1−sigmoid) ,那么其最大值才为0.25，而对于处于接近0或者接近1的地方导数值最后为0；如果此时进行梯度反向传播由于梯度为零导致模型的参数很难被更新。所以需要网络对于某一层的输出将数据的分布进行调整，让数据的分布分布在对于倒数不敏感的区域（也就是那些求导之后倒数不接近0的地方）。就如同下面的图示一样：
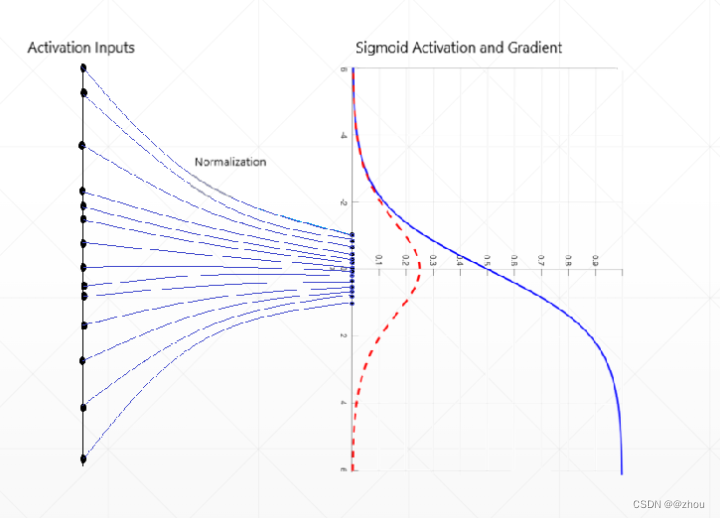
在这里插入图片描述

我们观察左边带有黑色点的图示其表示着数据的分布，同时看右边的蓝色实线代表着sigmoid的曲线，红色虚线代表倒数曲线。我们发现随着数据分布变得越来越分散那么倒数越来越小，而经过Normalization之后数据分布在0周围，同时也没有那么的分散，每一个数据的倒数此时也都不是接近于0。
下面给出Batchnorm的示意图：
在这里插入图片描述

好了简单的讲解了Batchnorm的来源，而在实际应用中我们只需要了解该类是如何运行的，其里面的参数有什么意义，并且了解在测试和训练时有什么不同。下面我分为数据准备，训练，测试三个方面讲解相关的内容。

数据准备

首先导入所需包，并且创建一个4D的数据，根据pytorch的官网需要一个4D的输入。

import torch
import torch.nn as nn
data = torch.rand(10,16,10,10) #batch * channels * h * w， 0-1均匀分布，均值0.5，方差1/12
bat_norm = nn.BatchNorm2d(16) #建立这个Batchnorm2d的类

CLASS torch.nn.BatchNorm2d(num_features,eps=1e-05,momentum=0.1,affine=True,track_running_stats=True,device=None,dtype=None)

关于这个类的使用：我们一般只需要传入的参数就是第一个num_features。其他的参数可以不需要关心，但是还是介绍一下：

eps:就是上图中的 $ϵ$ ,用来保证分母不为0
affine: 代表一个布尔值，若为True,那么上面的
$γ, β$ 就是一个可训练的张量，可使用bat_norm.weight和bat_norm.bias来访问
track_running_stats:也是一个布尔值，就是是否追踪数据的平均值和方差，一般我们都将使其为True
momentum:就是一个动量，默认为0.1，这样的话我们每次调用一次norm方法就会更新running_mean和running_var
我们这里展示的仅仅是传入num_features,其他的默认参数都没有修改。初始化该网络之后将会产生四个tensor:

print(bat_norm.weights) #可训练， shape = （num_features），初始化是全部是1
print(bat_norm.bias) #可训练， shape = （num_features），全是0
print(bat_norm.ruunning_mean)  #不可训练， shape = （num_features），全是0,
print(bat_norm.running_var) #不可训练， shape = （num_features），全是1

训练时

训练的时候我们首先计算出来某一个Batch的均值mean和方差var，然后使用normalization公式将其数据更新，下面我们展示手动计算的结果和使用API得到的结果误差。
计算完数据之后，我们还需要更新上面的running_mean和running_var,这两个参数将来会用于测试数据。

#设置为训练模式
bat_norm.train()
#手动计算的过程
mean = data.mean(dim=(0,2,3))
var = data.var(dim=(0,2,3))
print(mean, var)
#首先计算数据的均值和方差，然后我们使用动量法更新running_mean和ruuning_var
a = bat_norm.running_mean
b = bat_norm.running_var
#使用动量法进行更新，momentum的用处
a = a * （1 - bat_norm.momentum） + bat_norm.momentum * mean
b = b * (1 - bat_norm.momentum) + bat_norm.momentum * var
#计算normed数据
norm_data2 = (data.permute(0, 2, 3, 1) - mean)/(torch.sqrt(var + bat_norm.eps)) * bat_norm.weight + bat_norm.bias
norm_data2 = norm_data2.permute(0, 3, 1, 2)

#使用batchnorm计算，在调用forward方法的时候也会对running_mean 和running_var进行更新，每调用一次更新一次
norm_data = bat_norm(data)

#测试norm_data和我们手动得到的结果存在多大的误差
print("errors: ", torch.abs(norm_data2 - norm_data).sum() / 16000)

#查看手动更新之后的running_mean和running_var与模型自己计算的误差
print("running_mean:" torch.abs(a - bat_norm.running_mean).sum() / 16)
print("running_var:" torch.abs(b - bat_norm.running_var).sum() / 16)

测试

测试的时候我们不需要计算批量数据的均值和方差，只需要使用running_mean和running_var进行normalization就行

bat_norm.eval()
new_data = torch.rand(2, 16, 10, 10)
norm = bat_norm(new_data)
norm2 = (new_data.permute(0, 2, 3, 1) - a)/(torch.sqrt(b + bat_norm.eps))
norm2 = norm2.permute(0, 3, 1, 2)
print(torch.abs(norm2 - norm2).sum().item() / 3200)