matlab矩阵随机投影,稀疏随机投影（aka Johnson Lindenstrauss变换）不保留2点之间的距离...

我试图使用随机投影的方法(基本上，减少维度，同时保持2点之间的欧几里德距离)，最近我在网上发现了一些代码(MEX为MATLAB文件)：稀疏随机投影(aka Johnson Lindenstrauss变换)不保留2点之间的距离

/*

* sjlt.c - Sparse Johnson-Lindenstrauss Transform

*

* Creates a random sparse Johnson-Lindenstrauss projection matrix.

* The columns are independent and each column has exactly s non-zero

* entries. All non-zero entries are independent Rademacher random

* variables. Details can be found in [1].

*

* The calling syntax is:

*

* projection = sjlt(rows, columns, sparsity)

*

* This is a MEX file for MATLAB.

*

* Depending on your compiler, you can compile the function using

* one of the following calls:

* $ mex CXXFLAGS='$CXXFLAGS -std=c++0x' COPTIMFLAGS='-O3 -DNDEBUG' -largeArrayDims sjlt.cpp

* or

* $ mex CXXFLAGS='$CXXFLAGS -std=c++11' COPTIMFLAGS='-O3 -DNDEBUG' -largeArrayDims sjlt.cpp

*

* Author: Tobias Pohlen

*

* References:

* [1] Jean Bourgain, Sjoerd Dirksen, and Jelani Nelson. "Toward a Unified

* Theory of Sparse Dimensionality Reduction in Euclidean Space",

* Symposium on Theory of Computing, 2015.

*/

#include "mex.h"

#include

std::random_device rd;

std::mt19937 g(rd());

// We use this in order to generate rademacher random variables

std::uniform_int_distribution rademacherDist(0, 1);

inline int rademacher()

{

return 2*rademacherDist(g) - 1;

}

/* Tries to extract an integer from arg */

mwSize getIntegerScalar(const mxArray* arg)

{

if (mxGetNumberOfElements(arg) == 1)

{

return mxGetScalar(arg);

}

else

{

mexErrMsgTxt("Integer scalar is not of size == [1 1].n");

}

}

/* Returns an integer from arg or 0 if the integer is negative */

mwSize getNonNegativeIntegerScalar(const mxArray* arg)

{

int res = getIntegerScalar(arg);

if (res < 0)

{

return 0;

}

else

{

return res;

}

}

/* Shuffles the array randomly */

void shuffle(

mwSize* array,

mwSize size,

std::uniform_int_distribution & indexDistribution)

{

for (mwSize i = 0; i < size; i++)

{

std::swap(array[i], array[indexDistribution(g)]);

}

}

/* Creates a sparse Johnson Lindenstrauss Transform of size numRows x numCols

* of sparsity.

*/

void createSJLT(

mwSize sparsity,

mwSize numRows,

mwSize numCols,

double *entries,

mwSize* rowIndices,

mwSize* colIndices)

{

// Create an array of row indices to shuffle. We use this in order

// to draw random rows without replacement

std::uniform_int_distribution rowDist(0, numRows-1);

mwSize* rowCache = (mwSize*) malloc(numRows*sizeof(mwSize));

for (mwSize i = 0; i < numRows; i++)

{

rowCache[i] = i;

}

// Fill the column indices and the entries (remember that the entries are

// just independent rademacher random variables)

mwSize colOffset = 0;

for (mwSize c = 0; c < numCols; c++)

{

// Shuffle the row indices

shuffle(rowCache, sparsity, rowDist);

for (mwSize s = 0; s < sparsity; s++)

{

entries[colOffset+s] = rademacher();

rowIndices[colOffset+s] = rowCache[s];

}

colIndices[c] = c*sparsity;

colOffset += sparsity;

}

colIndices[numCols] = numCols*sparsity;

free(rowCache);

}

/*

* This is the function called by MATLAB.

*/

void mexFunction(

int numLeftHandSide,

mxArray *pointerLeftHandSide[],

int numRightHandSide,

const mxArray *pointerRightHandSide[])

{

// Inputs:

// 1. number of rows

// 2. number of columns

// 3. sparsity (number of non-zeros per column)

if(numRightHandSide != 3)

{

mexErrMsgIdAndTxt(

"arrayProduct:numRightHandSide",

"Three inputs required.");

}

// Outputs:

// 1. SJLT matrix

if (numLeftHandSide != 1)

{

mexErrMsgIdAndTxt(

"arrayProduct:numLeftHandSide",

"One output required.");

}

// Read the inputs

int numRows = getNonNegativeIntegerScalar(pointerRightHandSide[0]);

int numCols = getNonNegativeIntegerScalar(pointerRightHandSide[1]);

int sparsity = getNonNegativeIntegerScalar(pointerRightHandSide[2]);

// The sparsity cannot be higher than the number of rows

if (sparsity > numRows)

{

sparsity = numRows;

}

// Create the outputs

pointerLeftHandSide[0] = mxCreateSparse(numRows,numCols,numCols*sparsity,mxREAL);

// Create the transformation

createSJLT(

sparsity,

numRows,

numCols,

mxGetPr(pointerLeftHandSide[0]),

mxGetIr(pointerLeftHandSide[0]),

mxGetJc(pointerLeftHandSide[0]));

}

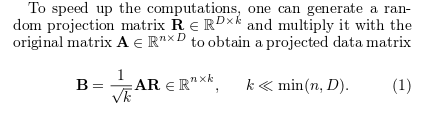
我理解的变量“s”是在每个列中的非零项的数量。反正，我已经写了MATLAB脚本测试如果这段代码确实保留2点之间的距离：奇怪的是不保留

>> mex CXXFLAGS='$CXXFLAGS -std=c++0x' COPTIMFLAGS='-O3 -DNDEBUG' -largeArrayDims sjlt.cpp

Building with 'g++'.

Warning: You are using gcc version '5.4.0'. The version of gcc is not supported. The version currently

supported with MEX is '4.7.x'. For a list of currently supported compilers see:

http://www.mathworks.com/support/compilers/current_release.

MEX completed successfully.

>> rng('default');

>> rng(1);

>> nObservations = 100;

>> nFeatures = 10000;

>> X = randn(nObservations, nFeatures);

>> X1 = X(1,:);

>> X2 = X(2,:);

>> dist = sqrt(sum((X1 - X2) .^ 2));

>> dist

dist =

142.1365

>> nFeatures_new = 3947; % This number was taken from: http://scikit-learn.org/stable/modules/random_projection.html

>> sparsity = 1;

>> R = sjlt(nFeatures, nFeatures_new,sparsity);

>> Y = X*R;

>> Y = (sqrt(sparsity)/sqrt(nFeatures_new)) * Y;

>> Y1 = Y(1,:);

>> Y2 = Y(2,:);

>> dist_transformed = sqrt(sum((Y1 - Y2) .^ 2));

>> dist_transformed

dist_transformed =

1.4397

的距离！由于存在警告(我使用的是ubuntu 16.04,64位版本)，因此必须出现错误，无论是使用代码还是使用编译.cpp文件的方式。谁能帮我？先谢谢你！