20201116
EX1 findLeafPage
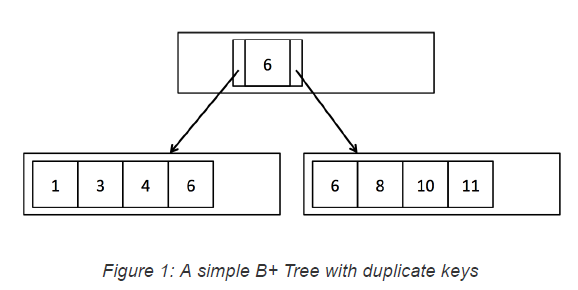
这张图已经比较明确的表示出了本练习的要求。主要包括一下的几个条件:
- 如果key为空,则返回最左侧的叶节点
- 否则进行依次与内部节点的entry中的key进行比较,返回可能的左侧节点,或者右侧节点。
- 如图中的情况,如果key为5,则返回左侧的叶节点;如果key为6,可以存在于多个节点上,我们也只返回左侧节点;如果key为15,则返回右节点。
具体代码如下:
private BTreeLeafPage findLeafPage(TransactionId tid, HashMap<PageId, Page> dirtypages, BTreePageId pid, Permissions perm,
Field f)
throws DbException, TransactionAbortedException {
// some code goes here
// 如果是叶子节点,设置权限perm,并返回
if(pid.pgcateg() == BTreePageId.LEAF) {
return (BTreeLeafPage) getPage(tid, dirtypages, pid, perm);
}else{
// 对于internal节点
BTreeEntry entry;
BTreeInternalPage bTreeInternalPage = (BTreeInternalPage) getPage(tid, dirtypages, pid, perm);
Iterator<BTreeEntry> internalPageIterator = bTreeInternalPage.iterator();
// 判断是否有entry
if (internalPageIterator.hasNext()){
entry = internalPageIterator.next();
}else{
throw new DbException("no entry in this node");
}
BTreePageId nextId;
if(f == null){
// f = null的时候,返回最左节点
nextId = entry.getLeftChild();
}else{
// 否则需要和entry进行比较,找到刚好 >=f 的 entry
while (f.compare(Op.GREATER_THAN, entry.getKey()) && internalPageIterator.hasNext()) {
entry = internalPageIterator.next();
}
// 如果f <= entry 取 entry的左子结点, 否则取右节点
if (f.compare(Op.LESS_THAN_OR_EQ, entry.getKey())) {
nextId = entry.getLeftChild();
} else {
nextId = entry.getRightChild();
}
}
return findLeafPage(tid, dirtypages, nextId, perm, f);
}
}
测试
2 Insert
机翻:
可以使用上一练习的FindLeafPage()来找到一个叶子节点,并将新的节点插入到B+树中。但是,如果叶子节点已经满了,就不能直接插入,而是需将节点进行切分,形成两个新的节点。每次切分的时候,将会把第二个页的第一个tuple加入到父节点。内部节点如果也满了,需要继续切分,向上传递节点。所以这个过程可以使用递归来实现。
如果在递归过程中,root节点也需切分,那么我们就要创建一个新的内部节点作为rootPage, 然后更新BTreeRootPtrPage。另外,取父页时需要使用READ_WRITE权限。在这个过程中,你可能会用到getParentWithEmptySlots()。在leafPage分裂时,复制一份entry到父节点,内部节点分裂时,移动一个entry到父节点。
可使用getEmptyPage()来创建新页面,比如在新建根节点时。
我们希望您可以使用btreeLeafPage.iterator()和BTreeInternalPage.iterator()遍历每个页面中的tuple/entry。为了方便起见,我们还为这两种类型的页面提供了反向迭代器:BTREEAFPage.reverseIterator()和InternalPage反向器() . 这些反向迭代器可以将tuple/entry的子集从页面移动到它的右同级。
如上所述,内部页迭代器使用BTreeEntry.java中定义的接口,它有一个键和两个子指针。它还有一个recordId,用于标识底层页上键和子指针的位置。我们认为一次处理一个条目是与内部页面交互的一种自然方式,但是必须记住,底层页面实际上并不存储条目列表,而是存储m个键和m+1个子指针的有序列表。由于BTreeEntry只是一个接口,而不是实际存储在页面上的对象,因此更新BTreeEntry的字段不会修改底层页面。要更改页面上的数据,您需要调用BTreeInternalPage.updateEntry() . 此外,删除一个条目实际上只删除一个键和一个子指针,所以我们提供了这些函数BTreeInternalPage.deleteKeyAndLeftChild()和BTreeInternalPage.deleteKeyAndRightChild()以明确这一点。条目的recordId用于查找要删除的键和子指针。插入一个条目也只插入一个键和一个子指针(除非它是第一个条目),所以BTreeInternalPage.insertEntry()检查所提供项中的一个子指针是否与页上现有的子指针重叠,并且在该位置插入该项将保持键的排序顺序。
总结几个点:
- 使用getEmptyPage()函数创建新的节点
- getParentWithEmptySlots()必然会得到一个有空slot的页
- 使用findLeafPage函数寻找叶节点,并将新的tuple插入到B+Tree中。
- 如果节点没有满直接插入即可。
- 如果满了,就需要进行切分。包括叶节点和内部节点。
- 切分时,如果是叶子节点,key保留在分隔后的叶节点中,并创建一个新的entry插入到内部节点。
- 如果是内部节点,key直接更新到其父节点中,不在切分后的内部节点保留。
- 如果根节点满了,需要切分,并创建一个新的根节点。
- 分隔叶节点后,要注意更新叶节点的左右兄弟节点指针
- 分隔内部节点后,需要注意更新左右孩子节点指针,提供了函数updateParentPointer()更新指针,提供了函数deleteKeyAndRightChild() deleteKeyAndLeftChild()函数删除指针。
- 正反向迭代无所谓,不过反向迭代貌似确实好写一点
- 更新dirtyPages, BTree中插入或者删除的时候,可能会更新多个页面,这与heapFIle是不同的,也解释了当时为啥heapFile要用ArrayList返回dirtyPages。
关于指针:
- innerPage: 分裂时直接用需要转移的entry的右孩子节点,并使用updateParentPointer函数重新整理孩子节点即可。
- leafPage: 需要配置左右兄弟节点,需要注意兄弟右兄弟节点为空的情况。
EX 2 Splitting Pages
代码如下:
protected BTreeLeafPage splitLeafPage(TransactionId tid, HashMap<PageId, Page> dirtypages, BTreeLeafPage page, Field field)
throws DbException, IOException, TransactionAbortedException {
// some code goes here
//
// Split the leaf page by adding a new page on the right of the existing
// page and moving half of the tuples to the new page. Copy the middle key up
// into the parent page, and recursively split the parent as needed to accommodate
// the new entry. getParentWithEmtpySlots() will be useful here. Don't forget to update
// the sibling pointers of all the affected leaf pages. Return the page into which a
// tuple with the given key field should be inserted.
// 创建一个新叶节点
BTreeLeafPage newLeafPage = (BTreeLeafPage) getEmptyPage(tid, dirtypages, BTreePageId.LEAF);
Iterator<Tuple> entryIterator = page.iterator();
// 找到中间tuple的位置
int midIndex = page.getNumTuples() / 2;
Tuple t = page.getTuple(midIndex);
int index = 0;
// 以其为切分,将本页中的mid后的删除并加入新页
while(entryIterator.hasNext()){
Tuple tuple = entryIterator.next();
if (index >= midIndex) {
page.deleteTuple(tuple);
newLeafPage.insertTuple(tuple);
}
index++;
}
// 修改的两个页面 添加到dirtyPages
dirtypages.put(page.pid, page);
dirtypages.put(newLeafPage.pid, newLeafPage);
// 设置左右兄弟节点
BTreePageId rightPid = page.getRightSiblingId();
// 判断右兄弟是否为空,不是空的话需要设置其左右兄弟
if (rightPid != null){
BTreeLeafPage rightLeafPage = (BTreeLeafPage) getPage(tid, dirtypages, rightPid, Permissions.READ_WRITE);
newLeafPage.setRightSiblingId(rightPid);
rightLeafPage.setLeftSiblingId(newLeafPage.getId());
dirtypages.put(rightPid, rightLeafPage);
}
page.setRightSiblingId(newLeafPage.getId());
newLeafPage.setLeftSiblingId(page.getId());
// 需要复制到父节点的key
Tuple keyToUp = newLeafPage.getTuple(0);
// 使用getParentWithEmpty找到有空的父节点,否则需要进行切分
// getParentWithEmptySlots这个函数中,做了迭代操作,包括父节点为root且满的情况
BTreeInternalPage parentPage = getParentWithEmptySlots(tid, dirtypages, page.getParentId(), keyToUp.getField(keyField));
parentPage.insertEntry(new BTreeEntry(keyToUp.getField(keyField), page.pid, newLeafPage.pid));
// 设置父节点
newLeafPage.setParentId(parentPage.getId());
page.setParentId(parentPage.getId());
// 判断插入的tuple在新页还是旧页
if(field.compare(Op.LESS_THAN_OR_EQ, t.getField(keyField))){
return page;
}else{
return newLeafPage;
}
}
protected BTreeInternalPage splitInternalPage(TransactionId tid, HashMap<PageId, Page> dirtypages,
BTreeInternalPage page, Field field)
throws DbException, IOException, TransactionAbortedException {
// some code goes here
// 跟上面的逻辑基本上一样
BTreeInternalPage newInternalPage = (BTreeInternalPage) getEmptyPage(tid, dirtypages, BTreePageId.INTERNAL);
int midIndex = page.getNumEntries() / 2;
Iterator<BTreeEntry> entryIterator = page.iterator();
int index = 0;
BTreeEntry keyToUp = null;
while(entryIterator.hasNext()){
BTreeEntry entry = entryIterator.next();
if(index == midIndex) {
page.deleteKeyAndRightChild(entry);
keyToUp = entry;
}
if(index > midIndex) {
page.deleteKeyAndRightChild(entry);
newInternalPage.insertEntry(entry);
// 更新指针
updateParentPointer(tid, dirtypages, newInternalPage.getId(), entry.getRightChild());
}
index++;
}
if (keyToUp == null)
throw new DbException("there is something wrong");
updateParentPointer(tid, dirtypages, newInternalPage.getId(), keyToUp.getRightChild());
BTreeInternalPage parent = getParentWithEmptySlots(tid, dirtypages, page.getParentId(), keyToUp.getKey());
// emmm 这里直接设置左右节点并插入entry,如果先插入在设置更新的话,节点的类型不会变化,
// 应该是一个小bug 0.0, updateEntry目前没有更新子节点的类型,应该是要更新的
keyToUp.setLeftChild(page.getId());
keyToUp.setRightChild(newInternalPage.getId());
parent.insertEntry(keyToUp);
page.setParentId(parent.getId());
newInternalPage.setParentId(parent.getId());
// 修改的页面加入dirtyPages
dirtypages.put(page.getId(), page);
dirtypages.put(newInternalPage.getId(), newInternalPage);
dirtypages.put(parent.getId(), parent);
// 选择返回的页面·
if(field.compare(Op.LESS_THAN_OR_EQ, keyToUp.getKey())) {
return page;
}else{
return newInternalPage;
}
}
测试
最后
以上就是苹果小猫咪最近收集整理的关于SimpleDB lab3 EX1~2的全部内容,更多相关SimpleDB内容请搜索靠谱客的其他文章。








发表评论 取消回复