python实现《直觉模糊集决策与对策分析方法》08直觉模糊数的矩阵对策解法

77 阅读 0 评论 51 点赞

我是靠谱客的博主危机世界，最近开发中收集的这篇文章主要介绍python实现《直觉模糊集决策与对策分析方法》08直觉模糊数的矩阵对策解法，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

这是李登峰老师《直觉模糊集决策与对策分析方法》第九章支付值为直觉模糊数的矩阵对策及其解法。
第一种解法是截集解法，判断直觉模糊数a和b的大小，仅需要比较某一具体截集，而不必比较所有截集。相当于对两个直觉模糊数，套在同一个区间上比较大小。
因此基本思想是将直觉模糊数转化为截集形式，然后构造线性规划模型求解纳什均衡。
对于给出的算例进行独立重复实验。代码关键步骤有注释。

'''
'''
from scipy import optimize as op
import numpy as np
import pandas as pd
np.set_printoptions(suppress=True)
def getlinerx(a,b,l):
    c=np.array([(1+l)*0.25,(1+l)*0.25,(1-l)*0.25,(1-l)*0.25,0,0])
    A_ub=np.array([[1,0,0,0,-(175*(0.6-a)+180*a)/0.6,-(80*(0.9-a)+90*a)/0.9],
                    [1,0,0,0,-(150*(0.6-a)+156*a)/0.6,-(175*(0.6-a)+180*a)/0.6],
                    [0,0,1,0,-(190*(0.6-a)+180*a)/0.6,-(108*(0.9-a)+90*a)/0.9],
                    [0,0,1,0,-(158*(0.6-a)+156*a)/0.6,-(190*(0.6-a)+180*a)/0.6],
                    [0,1,0,0,-(180*(1-b)+175*(b-0.2))/0.8,-(90*(1-b)+80*(b-0.1))/0.9],
                    [0,1,0,0,-(156*(1-b)+150*(b-0.1))/0.9,-(180*(1-b)+175*(b-0.2))/0.8],
                    [0,0,0,1,-(180*(1-b)+190*(b-0.2))/0.8,-(90*(1-b)+100*(b-0.1))/0.9],
                    [0,0,0,1,-(156*(1-b)+158*(b-0.1))/0.9,-(180*(1-b)+190*(b-0.2))/0.8]])
    B_ub=np.array([0,0,0,0,0,0,0,0])
    A_eq=np.array([[0,0,0,0,1,1]])
    B_eq=np.array([1])
    x5=(0,1)
    x6=(0,1)
    x1=(None,None)
    x2=(None,None)
    x3=(None,None)
    x4=(None,None)
    res=op.linprog(-c,A_ub,B_ub,A_eq,B_eq,bounds=(x1,x2,x3,x4,x5,x6))
    return res.x
def getlinery(a,b,l):
    c=np.array([(1+l)*0.25,(1+l)*0.25,(1-l)*0.25,(1-l)*0.25,0,0])
    A_ub=np.array([[-1,0,0,0,(175*(0.6-a)+180*a)/0.6,(150*(0.6-a)+150*a)/0.6],
                    [-1,0,0,0,(80*(0.9-a)+90*a)/0.9,(175*(0.6-a)+180*a)/0.6],
                    [0,0,-1,0,(190*(0.6-a)+180*a)/0.6,(158*(0.6-a)+156*a)/0.6],
                    [0,0,-1,0,(100*(0.9-a)+90*a)/0.9,(190*(0.6-a)+180*a)/0.6],
                    [0,-1,0,0,(180*(1-b)+175*(b-0.2))/0.8,(156*(1-b)+150*(b-0.1))/0.9],
                    [0,-1,0,0,(90*(1-b)+80*(b-0.1))/0.9,(180*(1-b)+175*(b-0.2))/0.8],
                    [0,0,0,-1,(180*(1-b)+190*(b-0.2))/0.8,(156*(1-b)+150*(b-0.1))/0.9],
                    [0,0,0,-1,(90*(1-b)+100*(b-0.1))/0.9,(180*(1-b)+190*(b-0.2))/0.8]])
    B_ub=np.array([0,0,0,0,0,0,0,0])
    A_eq=np.array([[0,0,0,0,1,1]])
    B_eq=np.array([1])
    x5=(0,1)
    x6=(0,1)
    x1=(None,None)
    x2=(None,None)
    x3=(None,None)
    x4=(None,None)
    res=op.linprog(c,A_ub,B_ub,A_eq,B_eq,bounds=(x1,x2,x3,x4,x5,x6))
    return res.x
if __name__ == '__main__':
    print(pd.DataFrame([getlinerx(0,1,0.1),getlinerx(0.1,0.8,0.1),getlinerx(0.2,0.7,0.1),getlinerx(0.3,0.6,0.1),
           getlinerx(0.4,0.5,0.1),getlinerx(0.5,0.3,0.1),getlinerx(0.6,0.2,0.1)]))
    print(pd.DataFrame([getlinery(0,1,0.1),getlinery(0.1,0.8,0.1),getlinery(0.2,0.7,0.1),getlinery(0.3,0.6,0.1),
           getlinery(0.4,0.5,0.1),getlinery(0.5,0.3,0.1),getlinery(0.6,0.2,0.1)]))

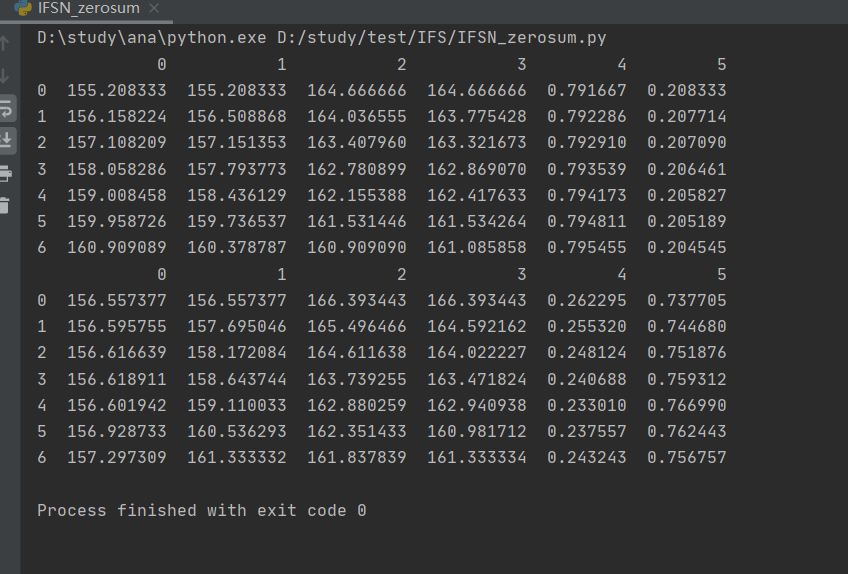
在这里插入图片描述
github仓库在https://github.com/rivendelltom/decision-making-study
第二种方法是加权均值面积解法。基本思想是分别求出隶属度和非隶属度的面积，然后使用线性加权的方法，将隶属度和非隶属度结合起来成为一个目标进行求解。
加权均值面积综合反映了直觉模糊数的隶属度和非隶属度在不同置信水平上的信息。有些决策者比较关心隶属度程度，有些决策者比较关心非隶属度程度，这样可以根据其偏好信息选取适当的加权值。算例很简单没有实现。