机械手位置控制之欧拉-拉格朗日方程仿真
- 问题背景
- 控制率设计
- 仿真参数
- 仿真结果
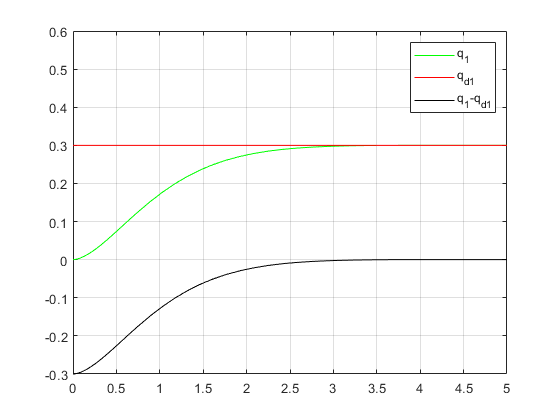
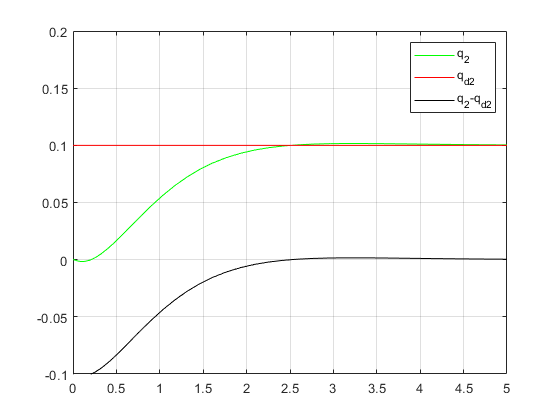
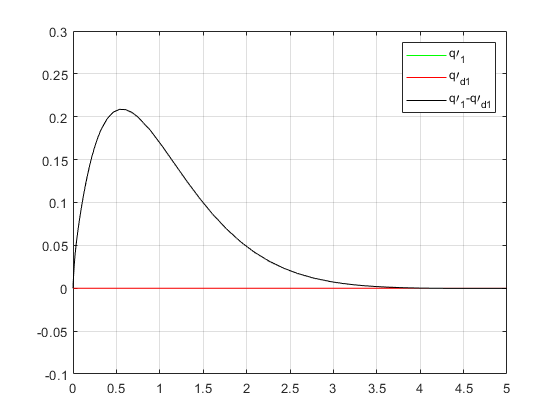
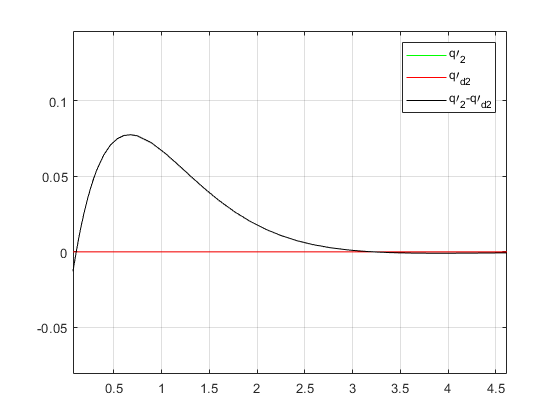
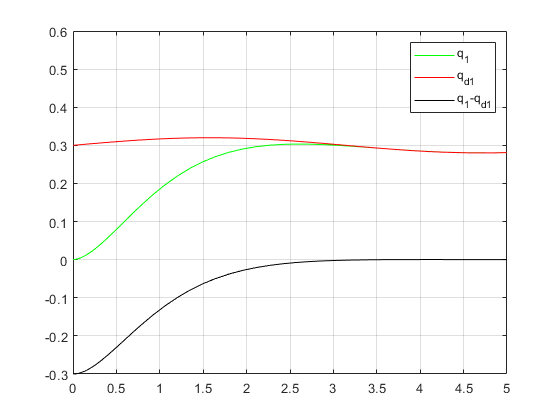
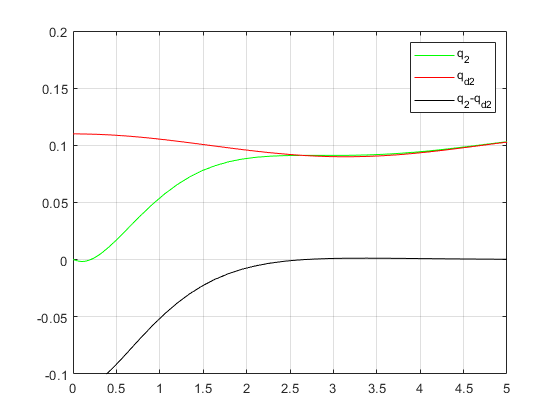
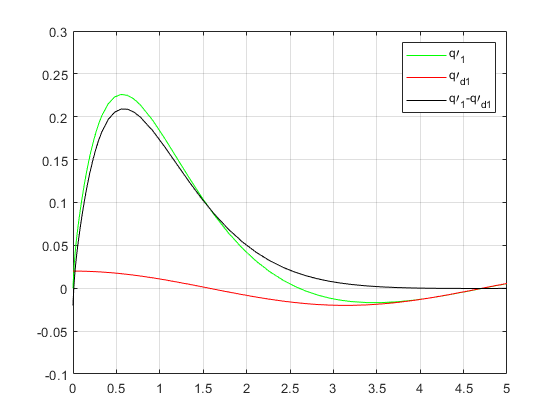
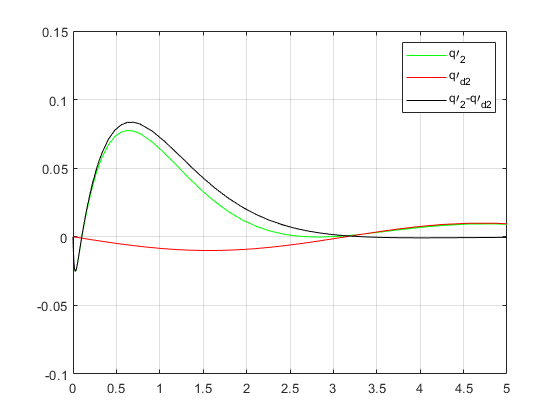
- (a)第一组期望位置仿真
- (b)第二组期望位置仿真
- 仿真方法说明
- 1.通过Matlab的内置函数求解
- 2.通过simulink仿真
- 3.采用迭代更新思想
问题背景
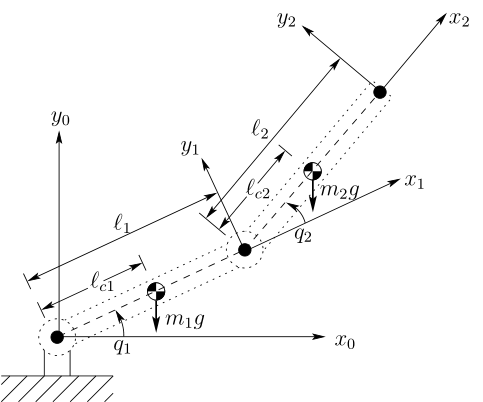
机械手的动态方程通常可以由欧拉-拉格朗日方程(Euler-Lagrange equation)描述,下面是一个简单的平面双铰链机械手的示意图。其中,坐标系 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)和 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)为机械手两个关节的轴坐标系,坐标系 ( x 2 , y 2 ) (x_2,y_2) (x2,y2)为机械手末端,实际应用中带负载使用,其位置可有由工作关节角度向量 q q q来描述,执行机构输入由作用于关节的两维力矩向量 τ tau τ组成,EL方程描述如下: M ( q ) q ¨ + C ( q , q ˙ ) q ˙ + g ( q ) = τ M(q)ddot{q}+C(q,dot{q})dot{q}+g(q)=tau M(q)q¨+C(q,q˙)q˙+g(q)=τ式中, M ( q ) M(q) M(q)为2x2维机械手惯量矩阵(对称正定), C ( q , q ˙ ) q ˙ C(q,dot{q})dot{q} C(q,q˙)q˙为两维向心和哥氏力矩向量 ( C ( q , q ˙ ) C(q,dot{q}) C(q,q˙)为2x2维矩阵), g ( q ) g(q) g(q)为两维重力力矩向量, q q q和 q ˙ dot{q} q˙分别为关节角度向量和关节速度向量。
至此,我们给出了描述该机械手的动力学的方程。那么接下来,我们的任务是实现机械手的位置控制和轨迹控制。显然,给定一组角度向量
q
q
q,我们可以唯一的确定机械手的位置,也就是说,要实现对机械手位置的控制,只需让
q
q
q按照我们期望的规律变化即可,也即跟踪问题。
控制率设计
对于机械手位置控制来说,我们可以采用比例-微分(PD)控制器来实现,即按照各关节测量误差
q
−
q
d
q-q_d
q−qd及其导数
q
˙
−
q
˙
d
dot{q}-dot{q}_d
q˙−q˙d来产生各关节执行机构的输入作用的反馈控制率,这里我们引入控制率如下
τ
=
−
K
1
(
q
−
q
d
)
−
K
2
(
q
˙
−
q
˙
d
)
+
M
(
q
)
q
¨
d
+
C
(
q
,
q
˙
)
q
˙
d
+
g
(
q
)
tau=-K_1(q-q_d)-K_2(dot{q}-dot{q}_d)+M(q)ddot{q}_d+C(q,dot{q})dot{q}_d+g(q)
τ=−K1(q−qd)−K2(q˙−q˙d)+M(q)q¨d+C(q,q˙)q˙d+g(q)其中,
K
1
K_1
K1和
K
2
K_2
K2为正定矩阵,通过调整
K
1
K_1
K1和
K
2
K_2
K2,可以调节系统的动态特性,这个在后面仿真时候可验证(此控制率除PD控制外,还引入了反馈线性化思想,cancel掉非线性项,若要具体推导可在后面评论回复)。在此控制率的作用下,我们可以通过Lyapunov函数验证系统状态误差是渐进收敛的,即可以跟踪上我们的期望位置
q
d
q_d
qd。
仿真参数
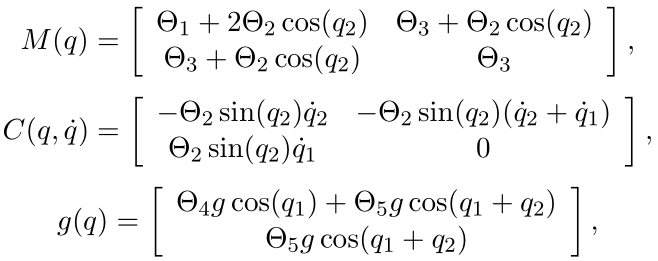
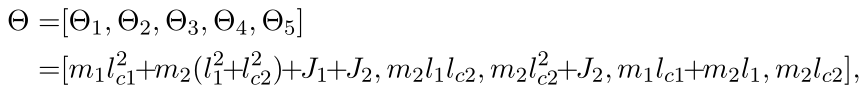
其中, m 1 = 1 k g m_1=1 kg m1=1kg, m 2 = 1.5 k g m_2=1.5kg m2=1.5kg, l 1 = 0.2 m l_1=0.2m l1=0.2m, l 2 = 0.3 m l_2=0.3m l2=0.3m, l c 1 = 0.1 m l_{c1}=0.1m lc1=0.1m, l c 2 = 0.15 m l_{c2}=0.15m lc2=0.15m, J 1 = 0.013 k g m 2 J_1=0.013kg m^2 J1=0.013kg m2, J 2 = 0.045 k g m 2 J_2=0.045kg m^2 J2=0.045kg m2
给定如下两个期望位置,我们通过上述控制率进行跟踪。
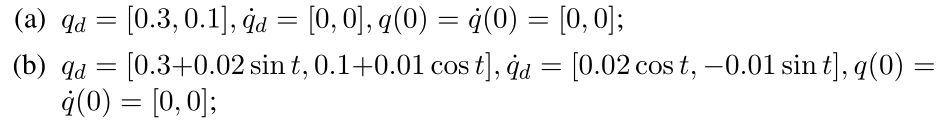
仿真结果
如下仿真我们假定了参数 K 1 K_1 K1和 K 2 K_2 K2均为单位阵,此时仿真结果如下:
(a)第一组期望位置仿真
(b)第二组期望位置仿真
仿真方法说明
对于菜鸟(本人)来说,上面的仿真整整做了几个小时,一方面是因为EL方程形式确实复杂,编程过程中多次输错下标导致程序崩溃。。。另外一个原因(重点),当然是菜鸟本尊。。。所以简单介绍一下微分方程的常用仿真方法,以帮助对此遇到问题的朋友。
1.通过Matlab的内置函数求解
Matlab内置了很多求解微分方程的函数(当然是数值解,函数dsolve用于求解解析解),具体可查阅相关资料了解。本文的仿真用的求解器是ode15s,即所谓的刚性微分方程变阶求解,其使用规条件及语法规则点击此处查看,或点击此处查看其英文文档,简单概括来说,就是ode15s允许奇异的惯量矩阵,同时可通过options定义绝对误差容忍限和相对误差容限。
下面给出一个简单的例程用于求解如下二阶微分方程:
y
¨
+
y
˙
+
y
=
c
o
s
t
y
(
0
)
=
0
y
˙
(
0
)
=
1
ddot{y}+dot{y}+y=cost qquad y(0)=0 dot{y}(0)=1
y¨+y˙+y=costy(0)=0 y˙(0)=1Matlab代码:
clc;
close all;
x0=[0 1];
dx=@(t,x)[x(2); cos(t)-x(1)-x(2)];
[t,x]=ode15s(dx,[0 10],x0);
plot(t, x(:,1));
其中,对于只有一个因变量的微分方程,x(1)表示 y y y,x(2)表示 y ˙ dot{y} y˙,cos(t)-x(1)-x(2)是用于描述 y ¨ ddot{y} y¨表达式。(若像此文仿真的微分方程中包含两个因变量,则x(1)表示 q 1 q_1 q1,x(2)表示 q ˙ 1 dot{q}_1 q˙1,x(3)表示 q 2 q_2 q2,x(4)表示 q ˙ 2 dot{q}_2 q˙2,dx=@(t,x)[x(2);表达式1;x(4);表达式2];其中表达式1和2分别为描述 q ¨ 1 ddot{q}_1 q¨1和 q ¨ 2 ddot{q}_2 q¨2的不带二阶项的表达式。)
2.通过simulink仿真
在应用第一种方法时,需要必要的手动化简,对于本文的仿真来说,要把 q ¨ 1 ddot{q}_1 q¨1和 q ¨ 2 ddot{q}_2 q¨2用不包含二阶导数项的表达式表示出来,也是花费一番功夫的,深有体会。。。所以simulink的好处就是不需要多少化简步骤,也避免了码代码时经常发生的下标标错导致程序崩溃的情况,只需要用框图把各个状态间的关系表示出来就可以了,当然最后得出的也是数值解。
同样对于这个二阶微分方程,我们给出其simulink仿真如下(第一个1/s初始值为1,第二个为0):
y
¨
+
y
˙
+
y
=
c
o
s
t
y
(
0
)
=
0
y
˙
(
0
)
=
1
ddot{y}+dot{y}+y=cost qquad y(0)=0 dot{y}(0)=1
y¨+y˙+y=costy(0)=0 y˙(0)=1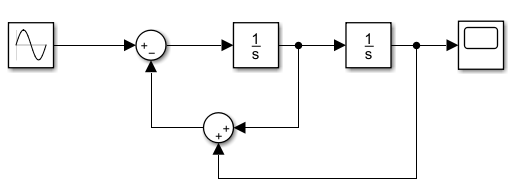
3.采用迭代更新思想
回忆我们手动求解微分方程时,给定微分方程,我们可以求解其通解,同时若给定了
n
n
n个初始条件(
n
n
n为方程阶数),我们可以求其特解。那么在用Matlab求解微分方程的数值解时,我们不要求给出其解析表达式(很多时候也是难以做到的),那么我们便可以通过迭代更新的思想来遍历我们感兴趣的解区间。举个简单的例子:
y
˙
=
c
o
s
t
y
(
0
)
=
0
dot{y}=costqquad y(0)=0
y˙=costy(0)=0
上面这个微分方程的解,虽然毫无疑问的就可以看出来了。。。但是,若是一个复杂的微分方程呢?
我们回到上面的例子,假设我们想求其在
(
0
,
1
)
(0,1)
(0,1)区间上的数值解,那么,采用微元法的思想,我们将此区间划分为很多小份,用
Δ
t
Delta t
Δt表示每一小份的长度,那么根据初始条件,我们便可以根据给定的微分方程求取
y
(
Δ
t
)
y(Delta t)
y(Δt)的函数值如下:
∫
0
Δ
t
y
˙
d
t
=
∫
0
Δ
t
c
o
s
t
d
t
int_0^{Delta t}dot{y} dt=int_0^{Delta t}cost dt
∫0Δty˙ dt=∫0Δtcost dt
那么我们便可以得到如下式子,其中
Δ
t
Delta t
Δt为我们手工选取的长度,比如
Δ
t
=
0.01
Delta t=0.01
Δt=0.01:
y
(
Δ
t
)
−
y
(
0
)
=
s
i
n
(
Δ
t
)
−
s
i
n
(
0
)
y(Delta t)-y(0)=sin(Delta t)-sin(0)
y(Δt)−y(0)=sin(Δt)−sin(0)
按照此思路,我们便可以得到在我们感兴趣区间的
y
y
y的数值解。
这种方法的仿真等之后有时间再更一次(马上上课去了…),大家也可以尝试自行编代码。
最后
以上就是粗心秀发最近收集整理的关于机械手位置控制——欧拉-拉格朗日方程仿真的全部内容,更多相关机械手位置控制——欧拉-拉格朗日方程仿真内容请搜索靠谱客的其他文章。








发表评论 取消回复