这部分的内容,我个人感觉主要是数学公式,稍微有一点难,不过没关系,我们从代码出发,再去理解数学公式

之前我们学习的是用函数去拟合Q-funtion,然后再根据Q值选择最佳策略,这节课讲的是直接拟合策略的方法,会用到策略梯度的方法

在第一节课的时候,科老师就提到了智能体agent的两种学习方案:

• 随机策略的方案 与 策略梯度的方案

随机策略与策略梯度

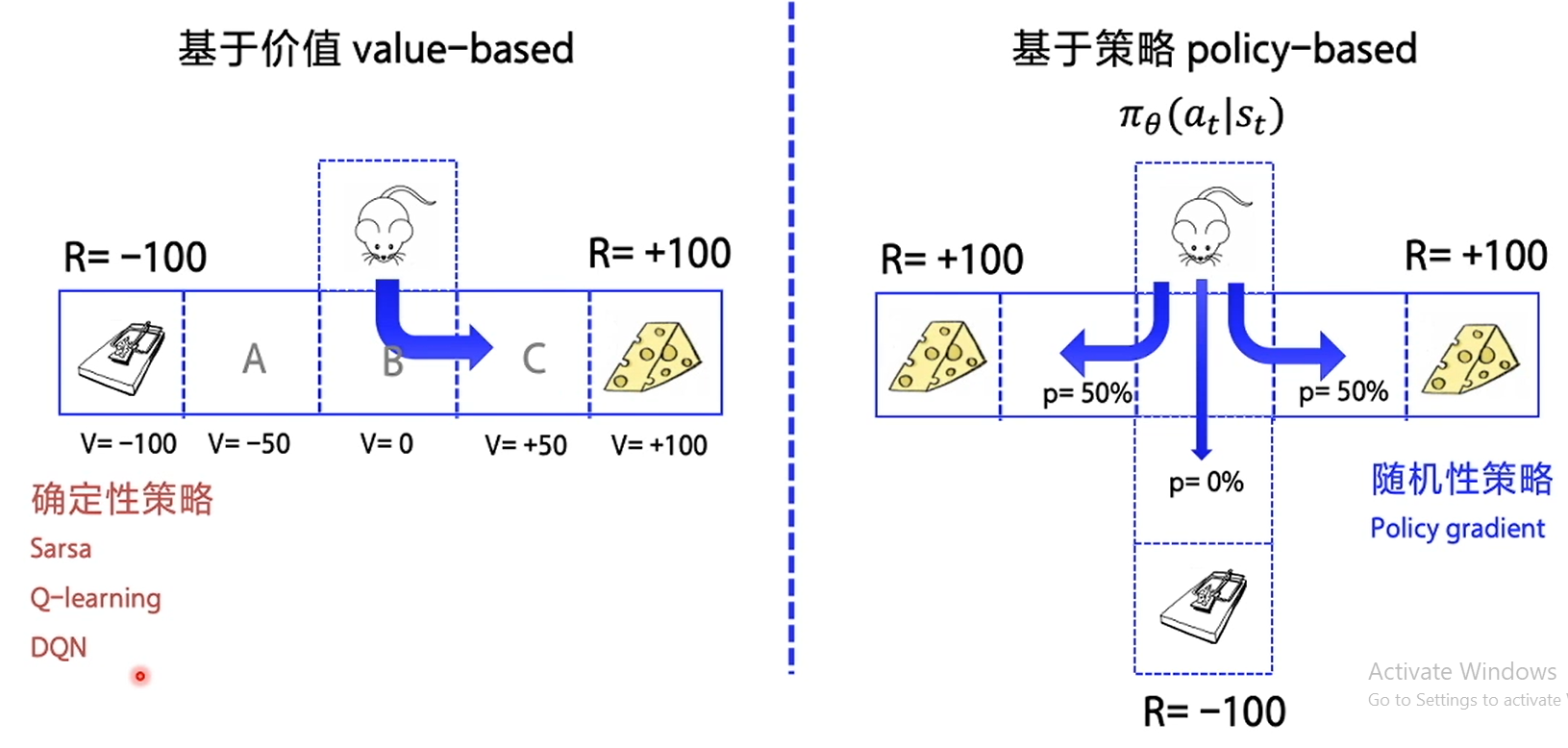
在强化学习中，有两大类方法，一种基于值（Value-based），一种基于策略（Policy-based）

• Value-based的算法的典型代表为Q-learning和SARSA，将Q函数优化到最优，再根据Q函数取最优策略。
• Policy-based的算法的典型代表为Policy Gradient，直接优化策略函数。

基于价值 value-based

value-based先学习动作价值函数,目的是把Q价值迭代更新到最优,然后再根据动作价值选择最优的动作

前面3节课讲的方法都是基于价值的方法

基于策略 policy-based

policy-based直接输出动作的概率,选择也不再依赖于价值函数,不会一个策略走到底,代表的算法就是今天要讲解的Policy Gradient

value-based VS policy-based

Policy-based直接表示策略

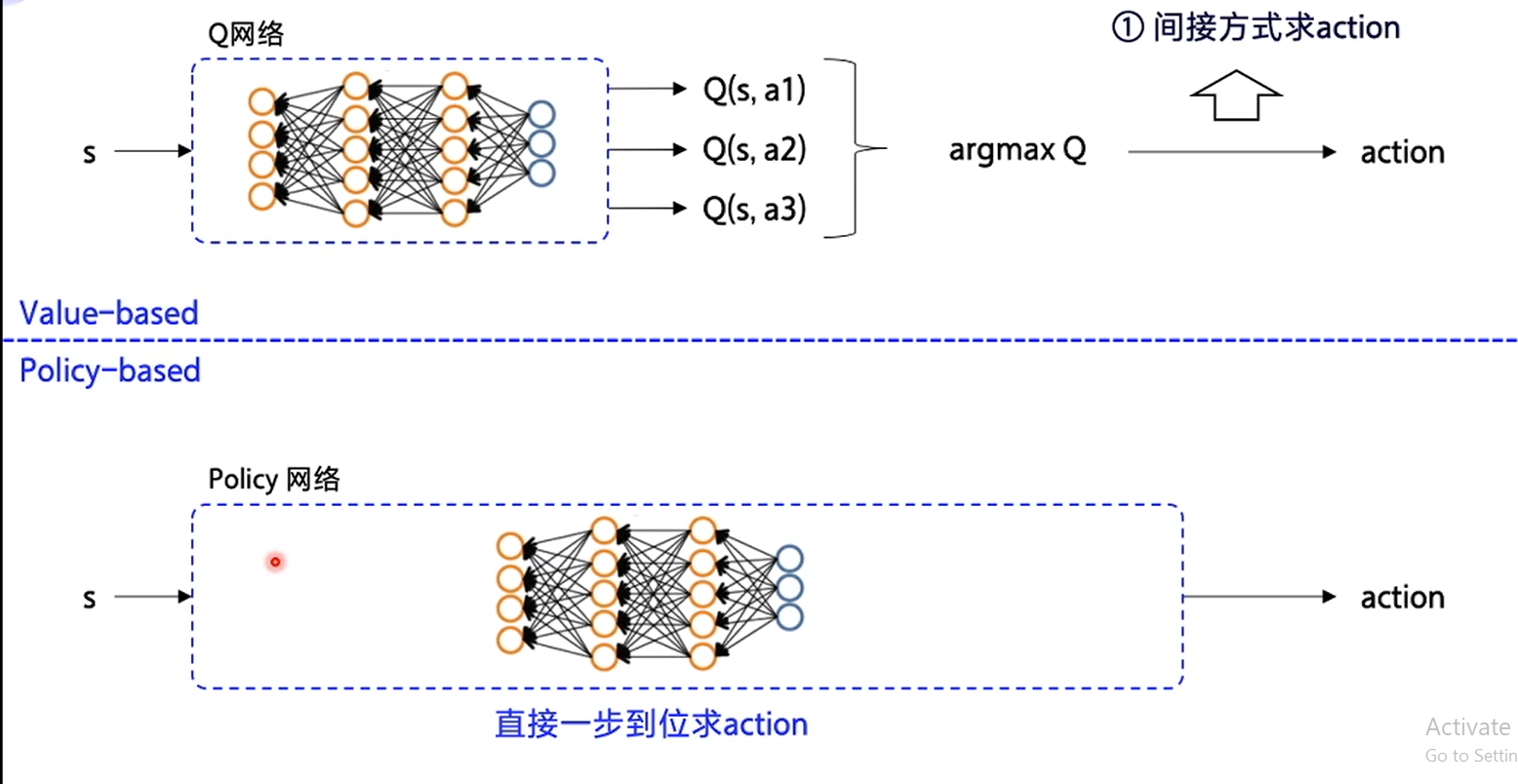
Value-base首先要求出Q值,然后优化的也一直是Q值,它把Q网络调到最优之后输出Q的最大值argmaxQ即输出Q值最大的动作

而Policy-based没有那么麻烦,不需要算哪个动作更值钱,直接用神经网络拟合一下policy,一步到位,输入x,输出动作action

随机策略

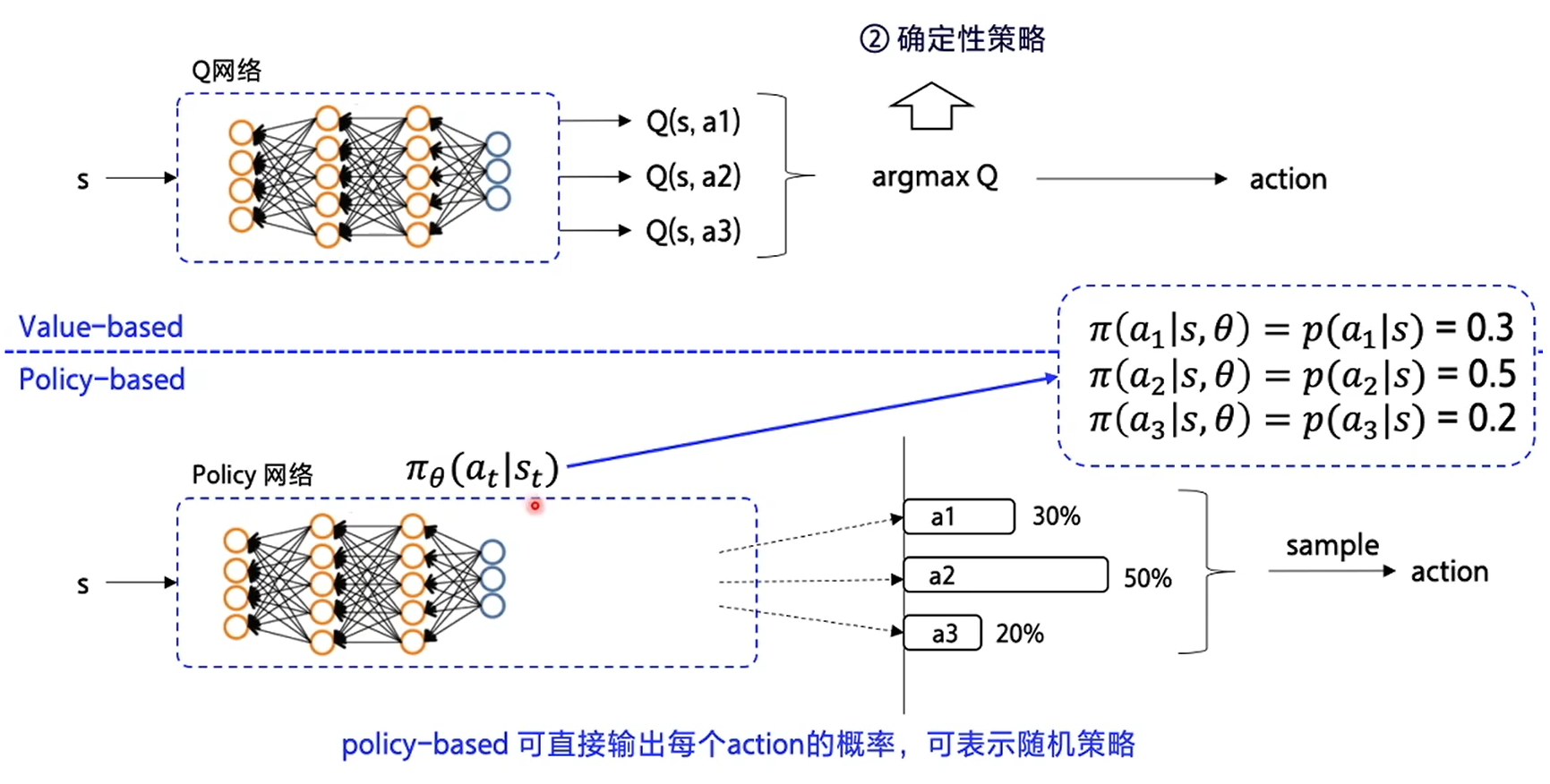
Value-base会先优化Q网络,把各个状态的动作价值都优化到最优了以后直接取出argmaxQ对应的动作,这样的做法其实是确定性的策略,输入一样的状态会得到一样的输出

而Policy-based输出的是动作的概率,它是随机的策略。用Π表示策略,θ表示神经网络的参数(权重、偏置等),${\Pi }_{\theta }(a_t|s_t)$表示的就是在$s_t$的状态下输出动作$a_t$的概率,假如只有3个动作,那么3个动作输出的概率相加应该为1,概率越大就越容易被采样到,也就越容易输出。这种策略在玩石头剪刀布这样的随机性很大的游戏中比较适用。

如果用DQN玩剪刀石头布这种随机性很大的游戏,很可能训练到最后,一直输出同一个动作。

但是用Policy Gradient的话,优化到最后就会发现三个动作的概率都是一样的,为了输出概率,一般都会在神经网络的最后加上一层softmax的全连接层

softmax函数

Softmax将多个神经元的输出，映射到(0, 1)区间内，可以看成概率来理解，可以输出不同动作的概率

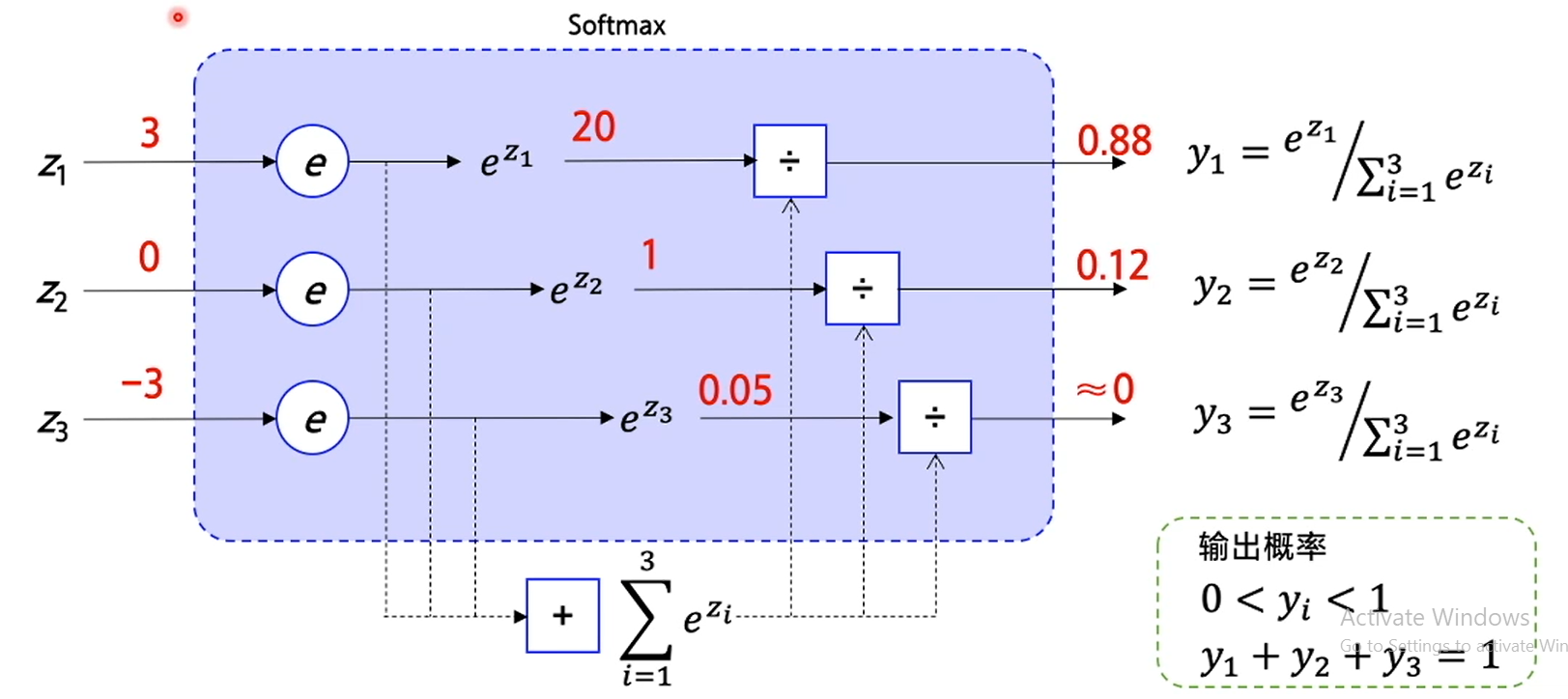
使用sortmax函数能保证输出是概率的同时,保证概率之和为1

随机策略举例

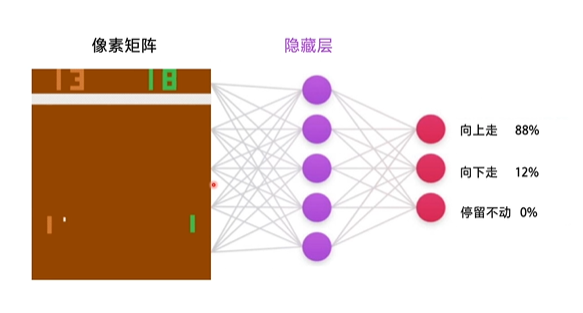
• 输入: 状态的像素矩阵
• 输出: 动作概率向量，比如[0.88, 0.12, 0.0]

在这个乒乓球游戏里,都是分幕的,一个episode(幕)代表一轮游戏

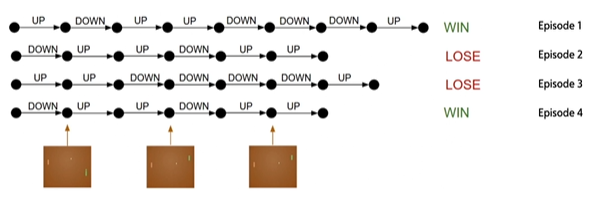
一个episode结束后才开始下一轮的游戏 ,最后的目的是让reward尽可能地大

也就是说,要尽可能地拉开得分的差距

那么,怎么去量化优化目标呢?

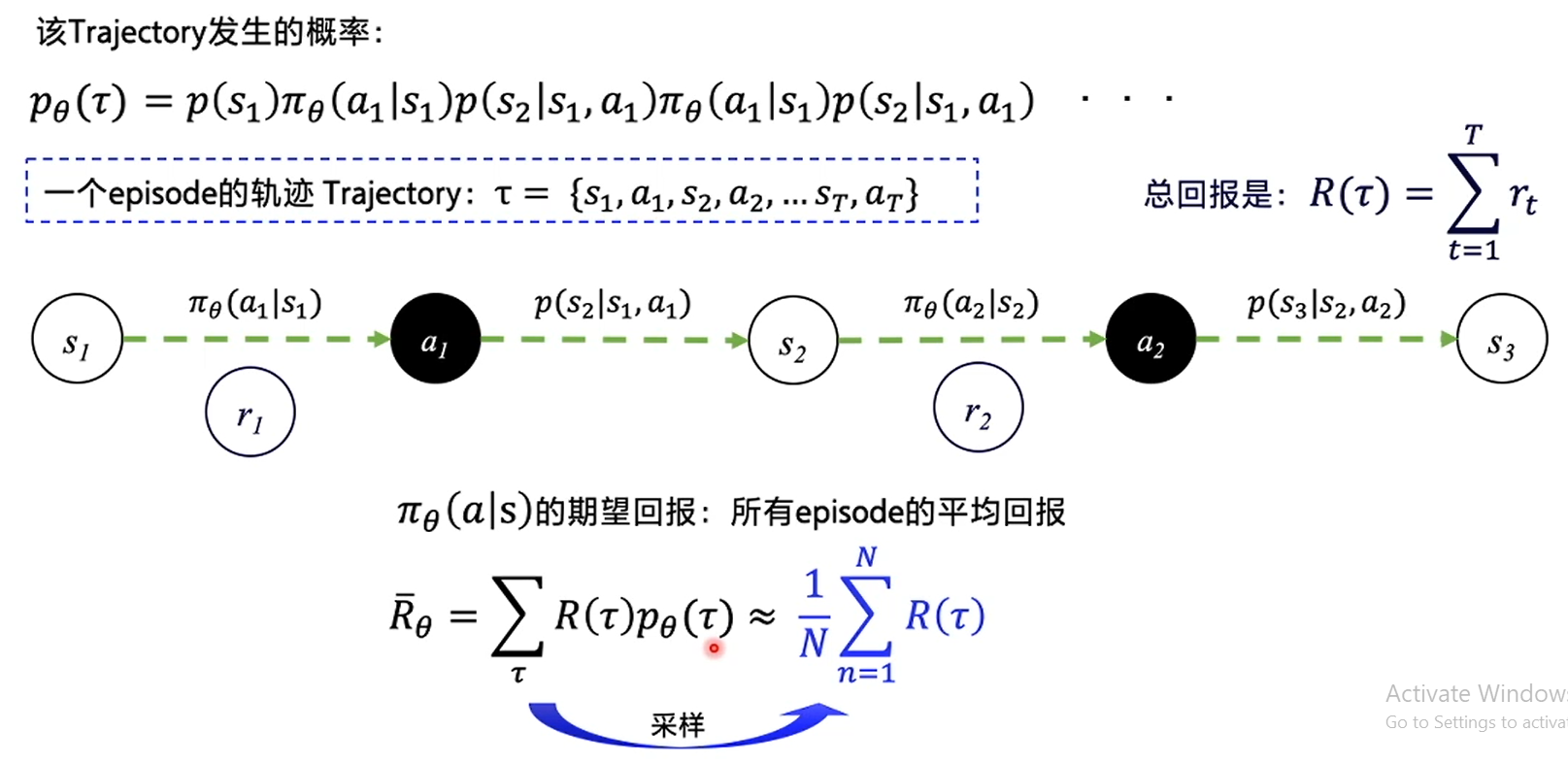
轨迹Trajectory

我们需要考虑所有的情况,从初始的状态出发,可能会有不同的概率选择不同的动作并用${\Pi }_{\theta }$表示输出的概率

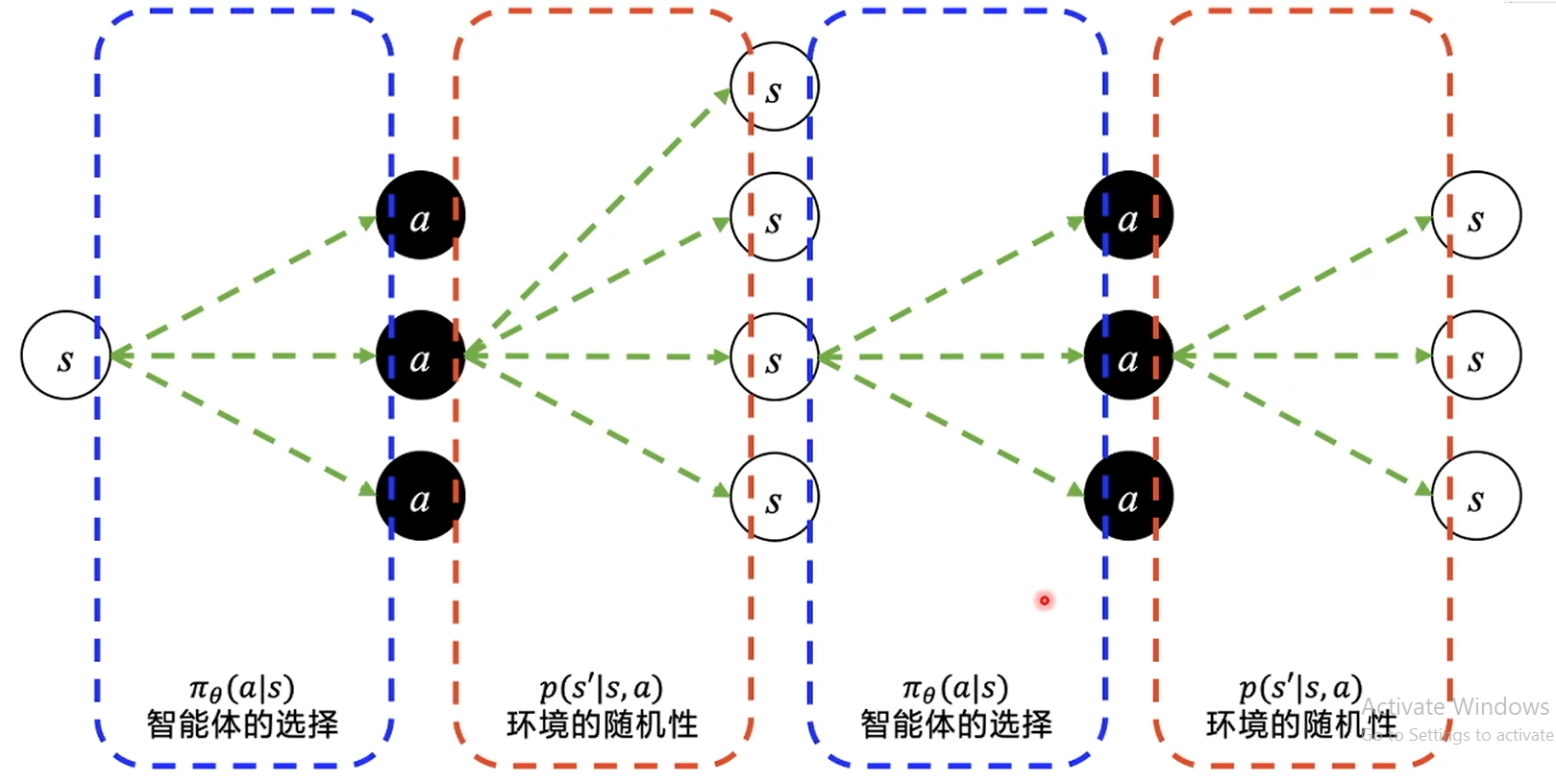
根据概率选择了其中一个动作之后,由于环境的随机性,会有不同的概率去到不同的状态,这个概率称为状态转移概率,用P来表示,$P(s^{\prime }|s,a)$表示在 s 状态下选择 a 动作后转移到状态 s’ 的概率。

去到一个新状态以后,又会交给智能体去选择,如此不断地交互下去… …

其中,智能体的选择是我们可以优化的策略,而环境转移概率不是我们能够控制的

期望回报

智能体只能跟环境交互后输出一个动作,再拿到一个新的状态,输出一个动作,当交互终止后,就算完成了一个episode:

把这一整个episode的状态和动作串起来的集合就叫做一个episode的轨迹Trajectory,那么我们也可以计算出这条轨迹发生的概率:

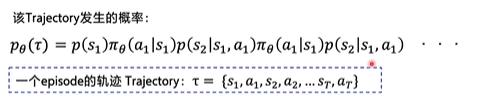
不光如此,我们还能计算出这条轨迹得到的总回报:

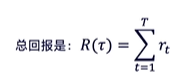
但实际上跟环境交互的轨迹不止一条,可能有千千万万条轨迹,所以可以把某一条轨迹拿到的分数(总回报)和这一条轨迹发生的概率相乘,然后再全部相加,便可以得到在策略Π下拿到的期望回报:

这在一定程度上可以反映出这条策略的好坏。

可是在正常的计算过程中,不可能把所有的轨迹都加起来,况且环境转移概率也是未知的,所以可以拿N个episode拿到的分数求平均,当N足够大的时候,可以近似地拟合期望回报:

这一过程称为采样,采样N个episode来计算近似的期望回报,这个期望回报可以用做优化策略函数的一个目标

优化策略函数

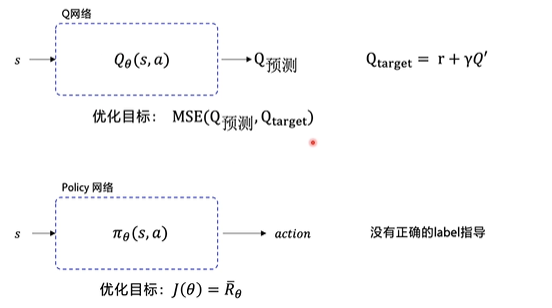
DQN构造的Q网络,是通过loss函数,也就是Qtarget和它的Q预测的平方差,而Qtarget其实担任的就是监督学习正确标签的角色

再看看Policy Gradient,输入状态state,输出动作action,但问题就在于没有正确的标签,谁也不知道在某个状态下最佳的动作是什么,所以Policy Gradient需要用到期望回报,它的目标是让期望回报越大越好,这个操作也叫做梯度上升

神经网络的参数更新需要根据梯度来决定参数更新的方向,也就是说,我们需要求解这个$R_{\theta }$,以此来更新网络

策略梯度

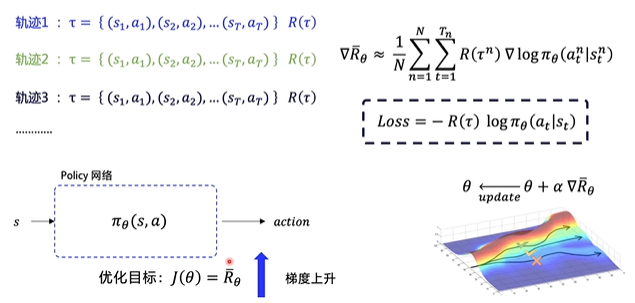
为了计算策略梯度,我们需要产生N条episode的轨迹,每一条轨迹都能算出一个回报,以及这条轨迹对应的梯度,优化目标对参数θ求导后得到策略梯度：

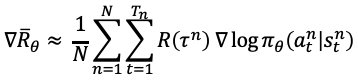
这个求导过程挺巧妙的,可以约去环境转移概率,这里没有做过多的推导,在后面会有详细的推导过程,写代码的时候,直接用这个公式写就可以了

为了达到梯度上升的效果,这里把loss计算出来以后,只需要在送进优化器前加一个负号即可起到梯度上升的效果了

PolicyGradeint算法

蒙特卡洛MC与时序差分TD

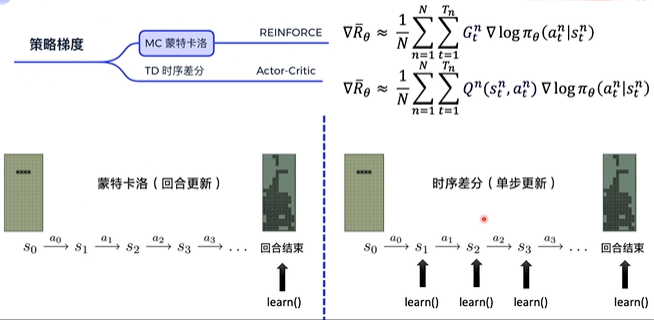
• 蒙特卡洛是在每个回合结束后去更新参数
• 时序差分是在每一个step后都做参数更新,它的更新频率更高

这里主要讲解REINFORCE算法

REINFORCE算法

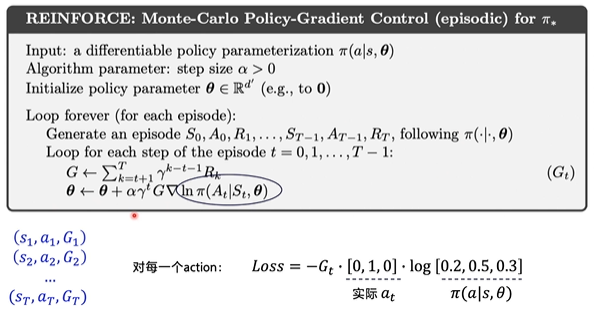
REINFORCE算法用的就是回合更新的方式

具体做法是先拿到一个episode的整个step的数据,然后把每一个动作的价值$G_t$算出来

# 根据一个episode的每个step的reward列表，计算每一个Step的Gt
def calc_reward_to_go(reward_list, gamma=1.0):
    for i in range(len(reward_list) - 2, -1, -1):
        # G_t = r_t + γ·r_t+1 + ... = r_t + γ·G_t+1
        reward_list[i] += gamma * reward_list[i + 1]  # Gt
    return np.array(reward_list)

类比监督学习来理解Policy Gradient

拿手写数字识别举例:

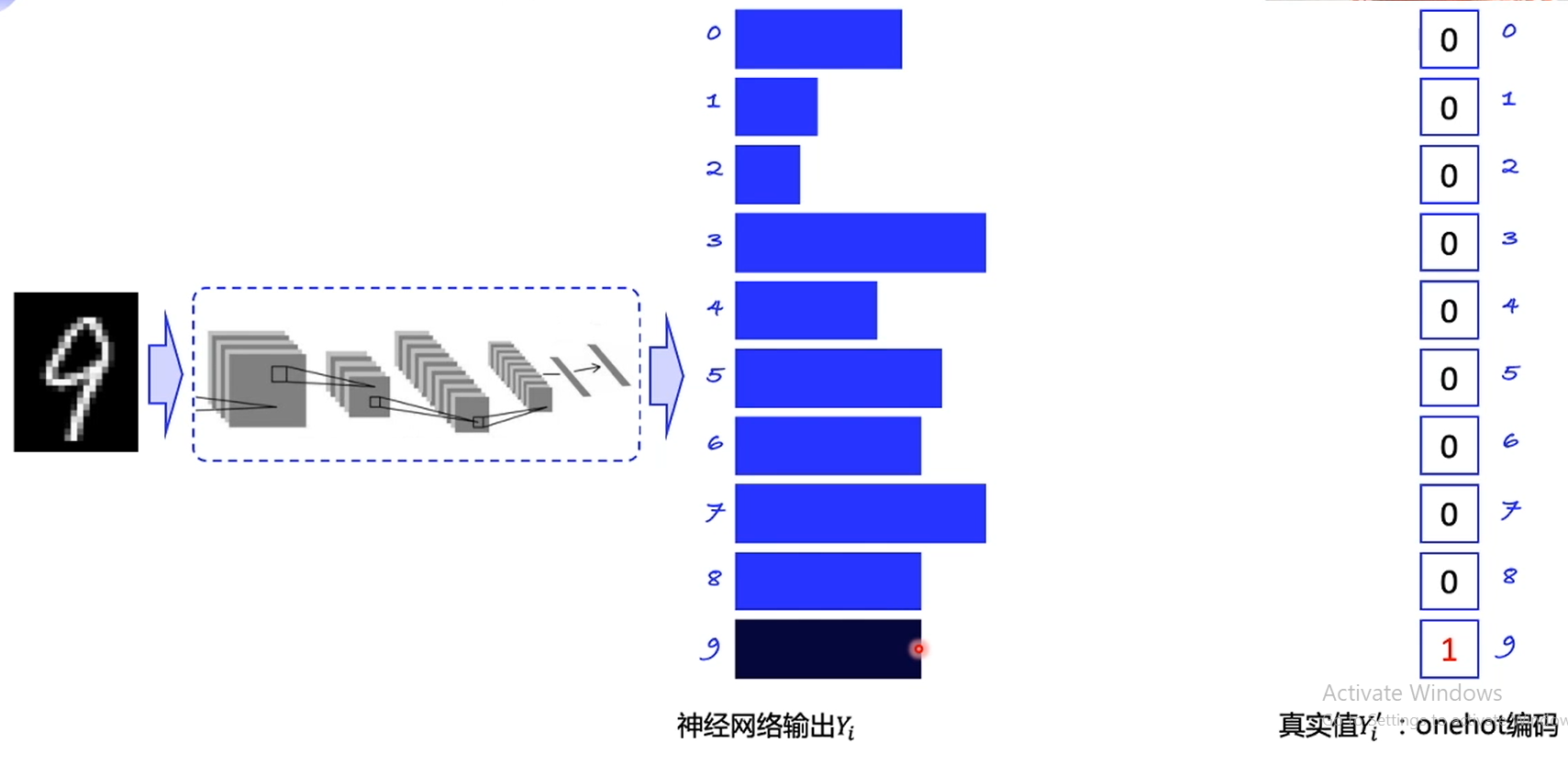
网络的输出是每一个数字的概率,预测的时候,选择概率最高的作为输出,但是训练时,要不断地优化概率,尽可能地使输出值的概率逼近1

可以用交叉熵来表示两个概率之间的差距,也就是神经网络的输出和真实值的差距:

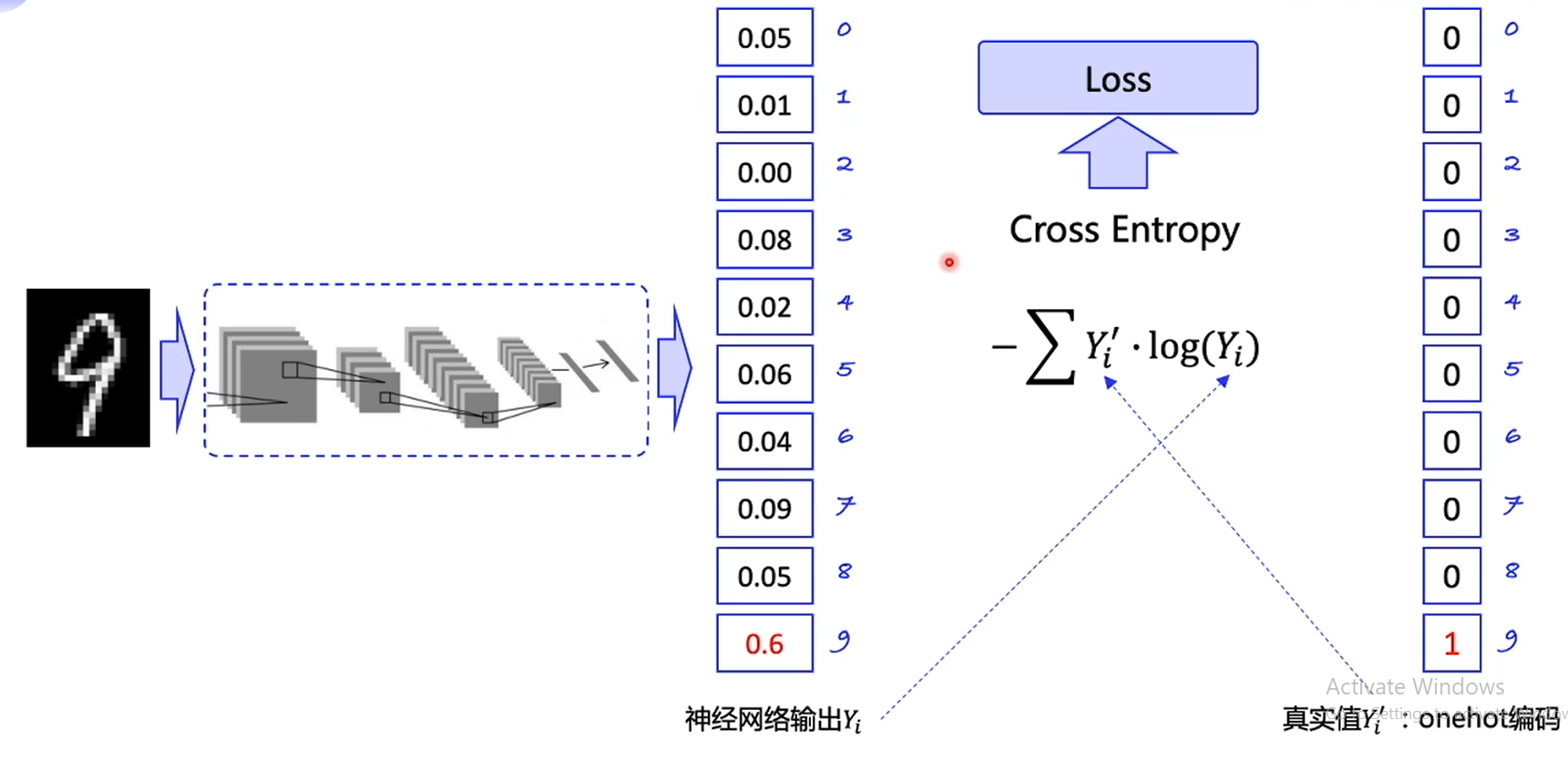
这个loss用来优化神经网络

那么类似的,Policy Gradient也可以这么做:

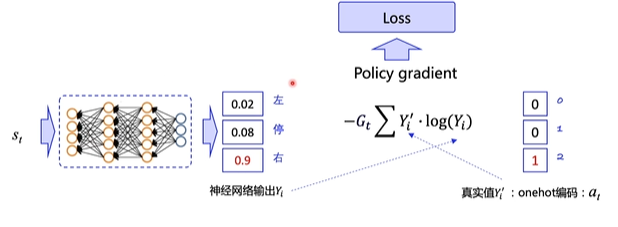
输入$s_t$,输出每个动作的概率分别为0.02、0.08和0.9,但实际上是选择其中一个动作输出,对应的概率是0、0、1

利用交叉熵,就可以求出输出的概率和实际输出的差距,但实际的动作$a_t$只是实际输出的action,它不一定是正确的action,他不能像手写数字识别那样,给出正确的标签,来指导神经网络朝着正确的方向更新参数,所以在这里要乘上一个奖励回报$G_t$

也就是加上$G_t$作为权重。$G_t$越大, loss越需要重视;$G_t$越小, loss就不那么重要

Loss

这就是我们要构造的loss:

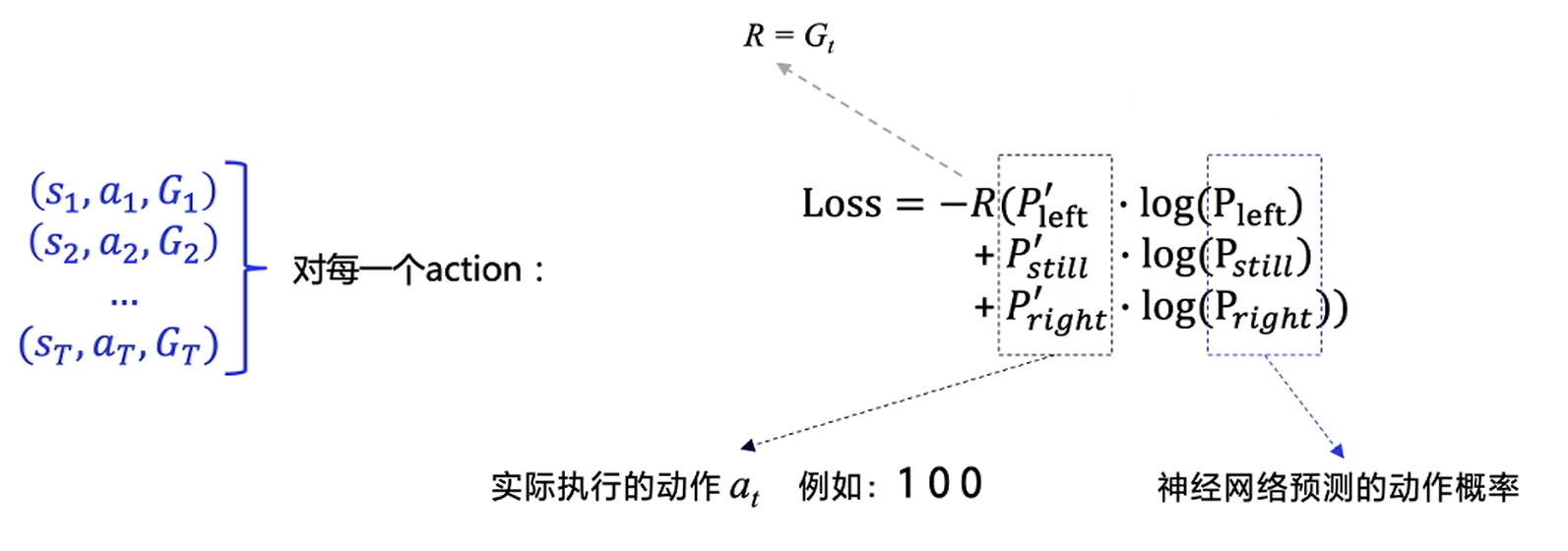
用代码可以表示为:

def learn(self, obs, action, reward):
        """ 用policy gradient 算法更新policy model
        """
        act_prob = self.model(obs)  # 获取输出动作概率
        # log_prob = layers.cross_entropy(act_prob, action) # 交叉熵
        log_prob = layers.reduce_sum(-1.0 * layers.log(act_prob) * layers.one_hot(action, act_prob.shape[1]),dim=1)
        cost = log_prob * reward
        cost = layers.reduce_mean(cost)

        optimizer = fluid.optimizer.Adam(self.lr)
        optimizer.minimize(cost)
        return cost

REINFORCE流程图

经过上面的介绍,再用流程图串起来:

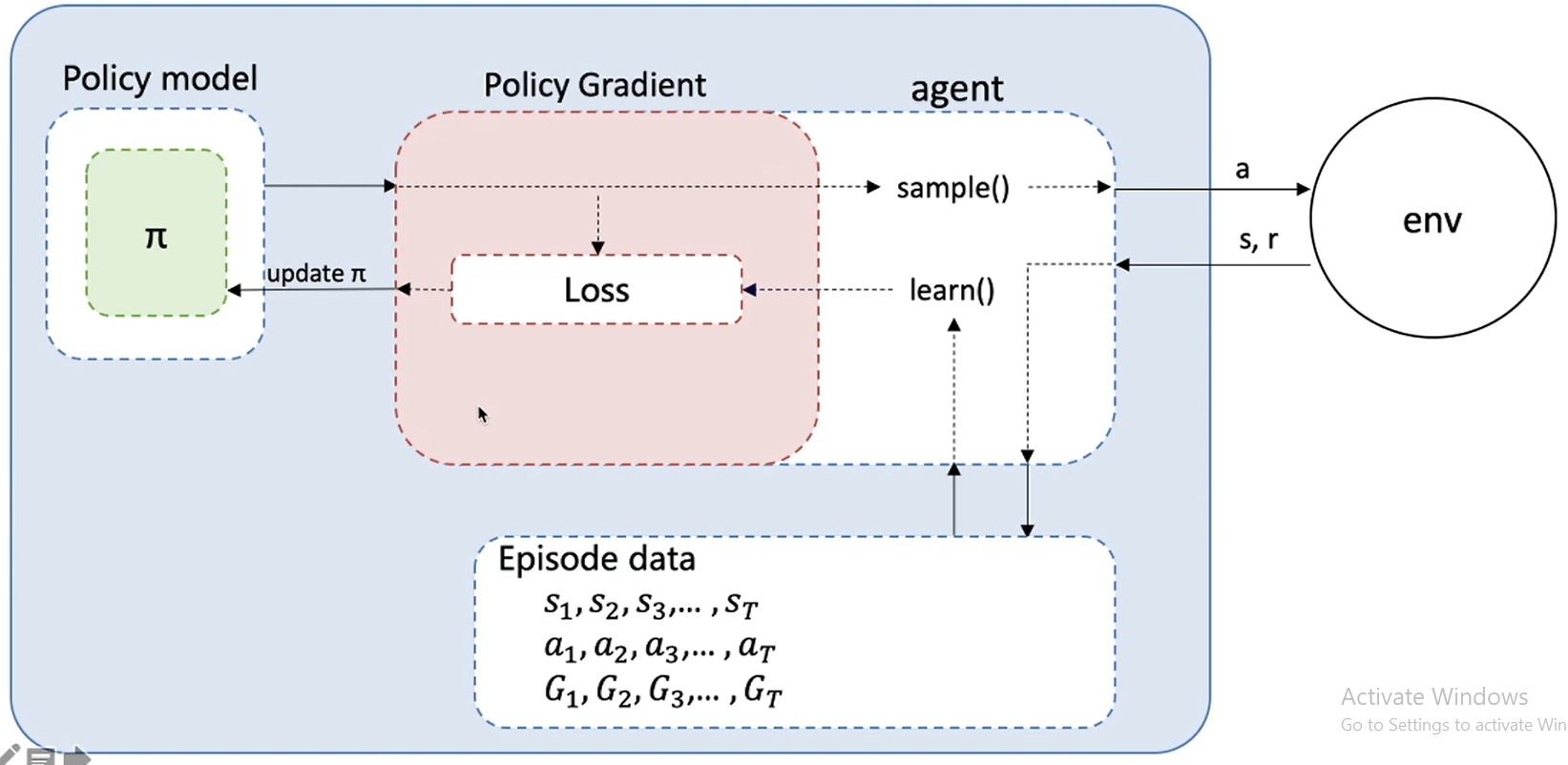
PARL Policy Gradient流程图:

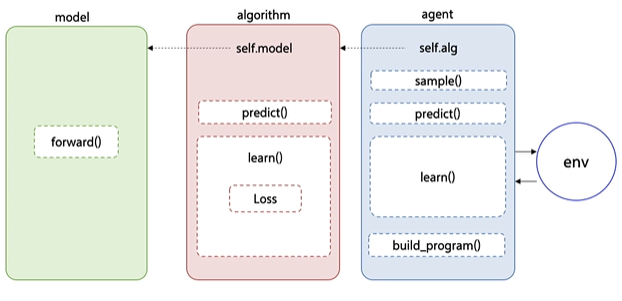
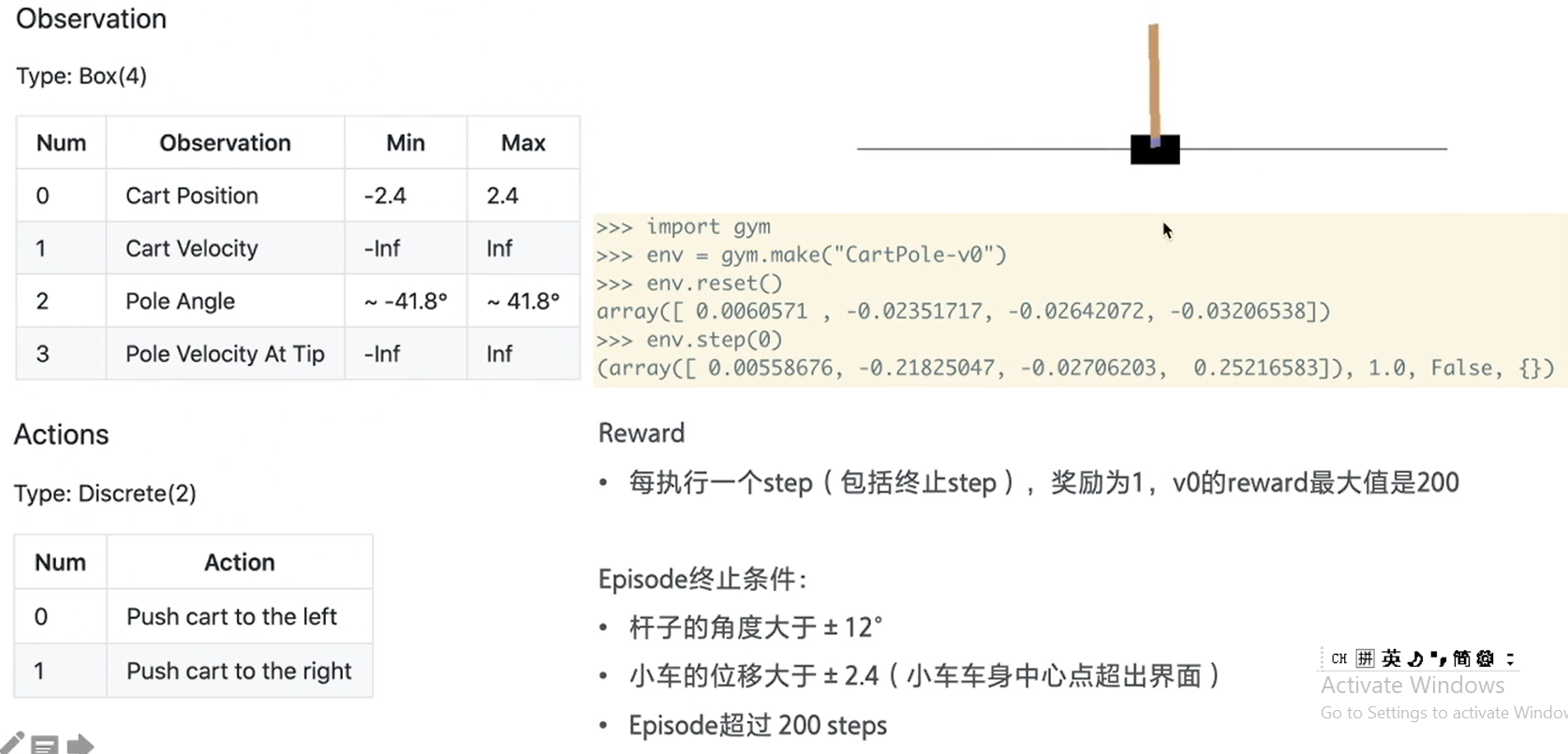
用Policy Gradient完成CartPole

CartPole的游戏规则是一样的

下面开始搭建Model、Algorithm、Agent架构

Model

Model用来定义前向(Forward)网络，用户可以自由的定制自己的网络结构。

class Model(parl.Model):
    def __init__(self, act_dim):
        act_dim = act_dim
        hid1_size = act_dim * 10

        self.fc1 = layers.fc(size=hid1_size, act='tanh')
        self.fc2 = layers.fc(size=act_dim, act='softmax')

    def forward(self, obs):  # 可直接用 model = Model(5); model(obs)调用
        out = self.fc1(obs)
        out = self.fc2(out)
        return out

这里需要注意的是最后一层全连接层的激活函数一定要用softmax,这样才会输出概率

Algorithm

Algorithm 定义了具体的算法来更新前向网络(Model)，也就是通过定义损失函数来更新Model，和算法相关的计算都放在algorithm中。

# from parl.algorithms import PolicyGradient # 也可以直接从parl库中导入PolicyGradient算法，无需重复写算法

class PolicyGradient(parl.Algorithm):
    def __init__(self, model, lr=None):
        """ Policy Gradient algorithm
        
        Args:
            model (parl.Model): policy的前向网络.
            lr (float): 学习率.
        """

        self.model = model
        assert isinstance(lr, float)
        self.lr = lr

    def predict(self, obs):
        """ 使用policy model预测输出的动作概率
        """
        return self.model(obs)

    def learn(self, obs, action, reward):
        """ 用policy gradient 算法更新policy model
        """
        act_prob = self.model(obs)  # 获取输出动作概率
        # log_prob = layers.cross_entropy(act_prob, action) # 交叉熵
        log_prob = layers.reduce_sum(
            -1.0 * layers.log(act_prob) * layers.one_hot(
                action, act_prob.shape[1]),
            dim=1)
        cost = log_prob * reward
        cost = layers.reduce_mean(cost)

        optimizer = fluid.optimizer.Adam(self.lr)
        optimizer.minimize(cost)
        return cost

Agent

Agent负责算法与环境的交互，在交互过程中把生成的数据提供给Algorithm来更新模型(Model)，数据的预处理流程也一般定义在这里。

class Agent(parl.Agent):
    def __init__(self, algorithm, obs_dim, act_dim):
        self.obs_dim = obs_dim
        self.act_dim = act_dim
        super(Agent, self).__init__(algorithm)

    def build_program(self):
        self.pred_program = fluid.Program()
        self.learn_program = fluid.Program()

        with fluid.program_guard(self.pred_program):  # 搭建计算图用于 预测动作，定义输入输出变量
            obs = layers.data(
                name='obs', shape=[self.obs_dim], dtype='float32')
            self.act_prob = self.alg.predict(obs)

        with fluid.program_guard(
                self.learn_program):  # 搭建计算图用于 更新policy网络，定义输入输出变量
            obs = layers.data(
                name='obs', shape=[self.obs_dim], dtype='float32')
            act = layers.data(name='act', shape=[1], dtype='int64')
            reward = layers.data(name='reward', shape=[], dtype='float32')
            self.cost = self.alg.learn(obs, act, reward)

    def sample(self, obs):
        obs = np.expand_dims(obs, axis=0)  # 增加一维维度
        act_prob = self.fluid_executor.run(
            self.pred_program,
            feed={'obs': obs.astype('float32')},
            fetch_list=[self.act_prob])[0]
        act_prob = np.squeeze(act_prob, axis=0)  # 减少一维维度
        act = np.random.choice(range(self.act_dim), p=act_prob)  # 根据动作概率选取动作
        return act

    def predict(self, obs):
        obs = np.expand_dims(obs, axis=0)
        act_prob = self.fluid_executor.run(
            self.pred_program,
            feed={'obs': obs.astype('float32')},
            fetch_list=[self.act_prob])[0]
        act_prob = np.squeeze(act_prob, axis=0)
        act = np.argmax(act_prob)  # 根据动作概率选择概率最高的动作
        return act

    def learn(self, obs, act, reward):
        act = np.expand_dims(act, axis=-1)
        feed = {
            'obs': obs.astype('float32'),
            'act': act.astype('int64'),
            'reward': reward.astype('float32')
        }
        cost = self.fluid_executor.run(
            self.learn_program, feed=feed, fetch_list=[self.cost])[0]
        return cost

然后在main()函数里:

# 创建环境
env = gym.make('CartPole-v0')
obs_dim = env.observation_space.shape[0]
act_dim = env.action_space.n
logger.info('obs_dim {}, act_dim {}'.format(obs_dim, act_dim))

# 根据parl框架构建agent
model = Model(act_dim=act_dim)
alg = PolicyGradient(model, lr=LEARNING_RATE)
agent = Agent(alg, obs_dim=obs_dim, act_dim=act_dim)

# 加载模型
# if os.path.exists('./model.ckpt'):
#     agent.restore('./model.ckpt')
#     run_episode(env, agent, train_or_test='test', render=True)
#     exit()

for i in range(1000):
    obs_list, action_list, reward_list = run_episode(env, agent)
    if i % 10 == 0:
        logger.info("Episode {}, Reward Sum {}.".format(
            i, sum(reward_list)))

    batch_obs = np.array(obs_list)
    batch_action = np.array(action_list)
    batch_reward = calc_reward_to_go(reward_list)

    agent.learn(batch_obs, batch_action, batch_reward)
    if (i + 1) % 100 == 0:
        total_reward = evaluate(env, agent, render=False) # render=True 查看渲染效果，需要在本地运行，AIStudio无法显示
        logger.info('Test reward: {}'.format(total_reward))

# 保存模型到文件 ./model.ckpt
agent.save('./model.ckpt')

以上的代码可以在PARL下的lesson4找到:

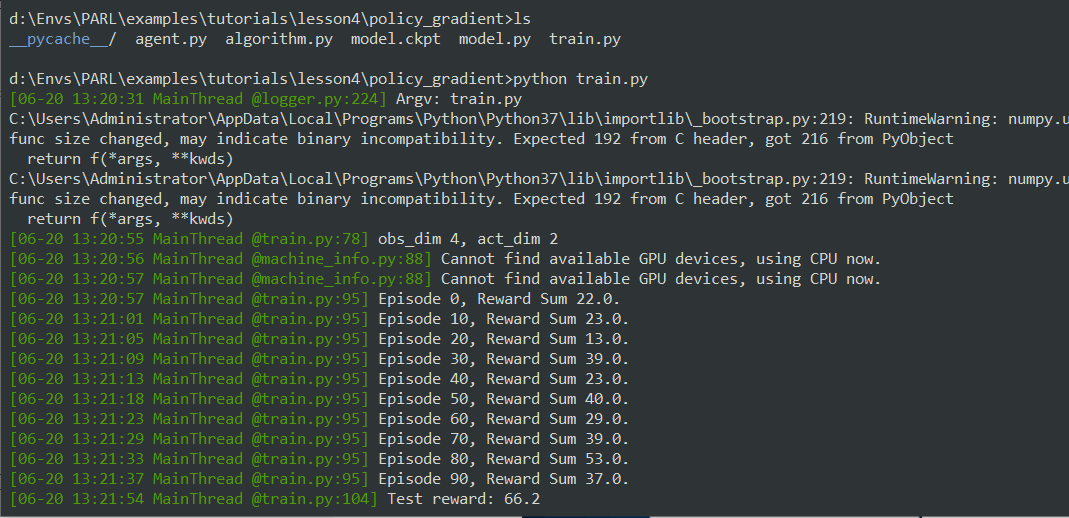
可以看到刚开始训练的时候,效果就很不错了:

公式推导

最后

以上就是懦弱煎饼为你收集整理的从零实践强化学习之基于策略梯度求解RL(PARL)随机策略与策略梯度PolicyGradeint算法公式推导的全部内容，希望文章能够帮你解决从零实践强化学习之基于策略梯度求解RL(PARL)随机策略与策略梯度PolicyGradeint算法公式推导所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。