目录
- 1.组合
- 2.组合总和 III
- 3. 电话号码的字母组合
- 4. 组合总和
- 5.组合总和 II
“回溯是递归的副产品,只要有递归就会有回溯。”
b站-回溯算法理论基础
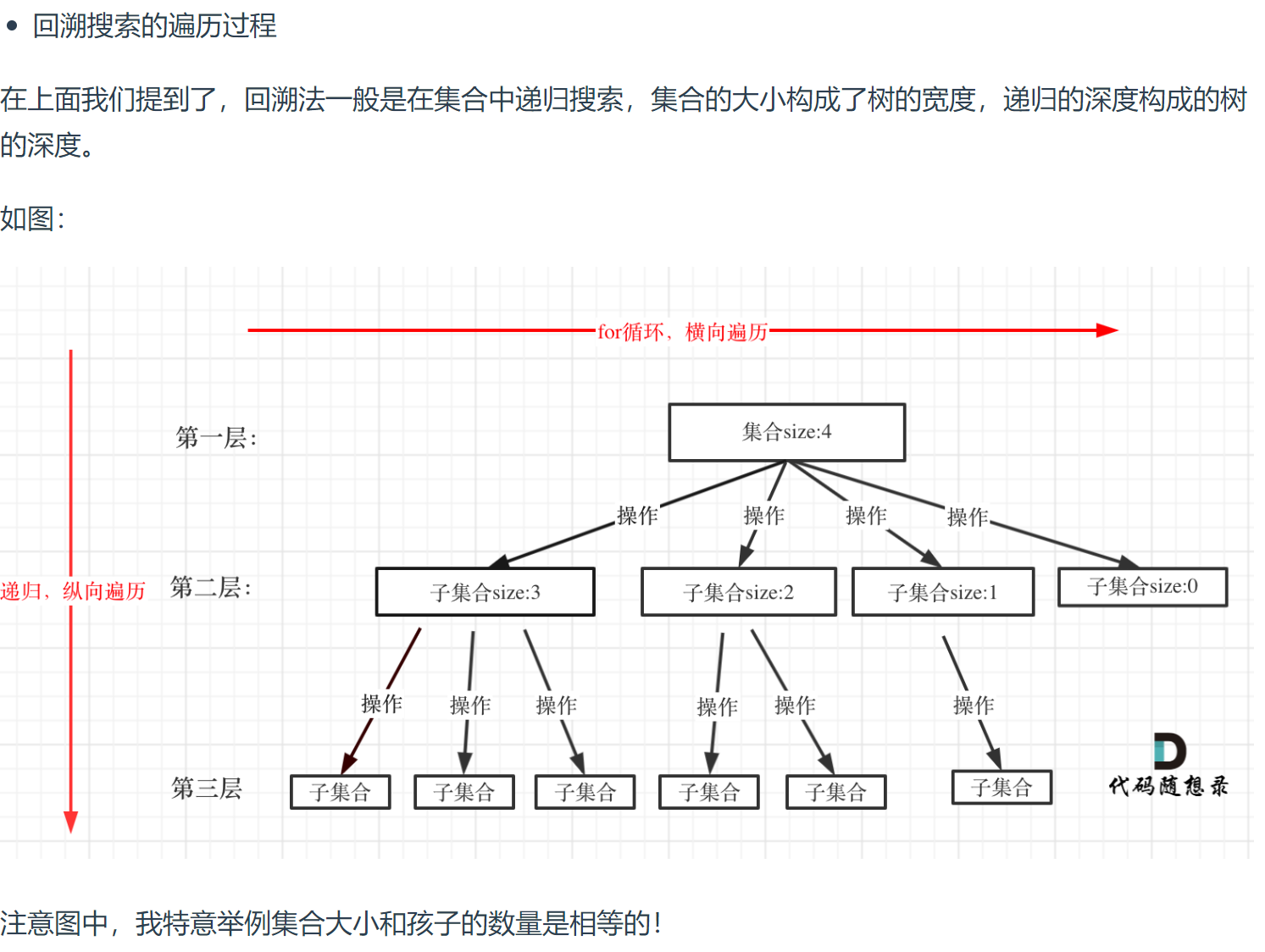
回溯其实就是纯暴力搜索,一些问题没法用for循环。
回溯可以解决:组合、切割、子集、排列、棋盘这类问题

1.组合
77. 组合-中等
b站-代码随想录
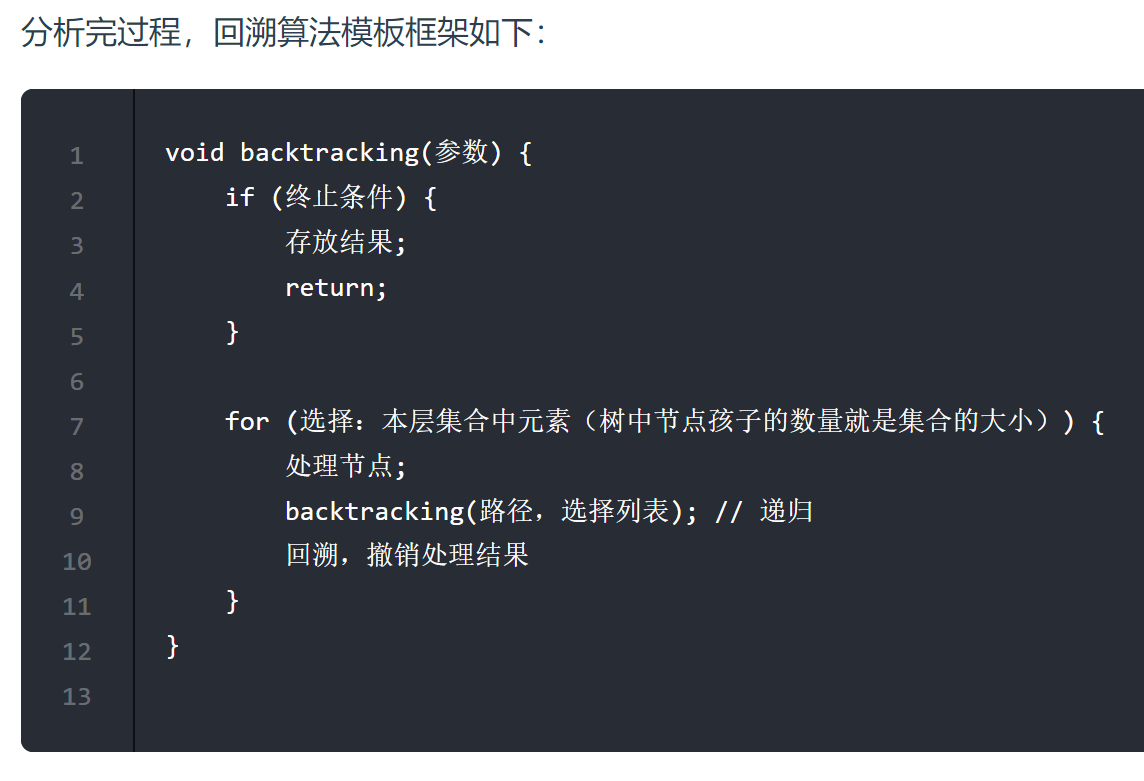
递归就是用来控制有多少层for循环。k=2时我们可以用两层for循环,那k=50时咋办呢?
回溯法????
var combine = function(n, k) {
const ans = [], path = [];
const backtracing = (n, k, startIndex) => {
if(path.length === k) {
ans.push(path.slice());
// res.push(Array.from(path));
// ans.push([...path]);
return;
}
for(let i = startIndex; i <= n; i++) {
path.push(i);
backtracing(n, k, i + 1);
path.pop();
}
}
backtracing(n, k, 1);
return ans;
};
剪枝????
可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。
i <= n - (k - path.length) + 1;
let result = []
let path = []
var combine = function(n, k) {
result = []
combineHelper(n, k, 1)
return result
};
const combineHelper = (n, k, startIndex) => {
if (path.length === k) {
result.push([...path])
return
}
for (let i = startIndex; i <= n - (k - path.length) + 1; ++i) {
path.push(i)
combineHelper(n, k, i + 1)
path.pop()
}
}
2.组合总和 III
216. 组合总和 III-中等
b站解答
确定终止条件:
path.length == ksum == n
var combinationSum3 = function(k, n) {
const ans = [], path = [];
let sum = 0;
const backtracing = (path, index) => {
// 剪枝
if(sum > n) {
return;
}
if(path.length === k) {
if(sum === n) {
ans.push([...path]);
return;
}
}
// for循环中也有剪枝
for(let i = index; i <= 9 - (k - path.length) + 1; i++) {
path.push(i);
sum = sum + i;
index++;
backtracing(path, index);
sum -= i;
path.pop();
}
}
backtracing(path, 1);
return ans;
};
3. 电话号码的字母组合
17. 电话号码的字母组合-中等
b站视频讲解
普通解法
var letterCombinations = function(digits) {
let ans=[],len=digits.length;
if(digits=="") return ans;
let inputMap = {"2":"abc","3":"def","4":"ghi","5":"jkl","6":"mno","7":"pqrs","8":"tuv","9":"wxyz"};
for(let i=0;i<len;i++){
ans[i]=[];
let c=inputMap[digits[i]];
for(let j=0;j<c.length;j++){
if(i==0){
ans[i].push(c[j]);
}else{
for(let k=0;k<ans[i-1].length;k++){
ans[i].push(ans[i-1][k]+c[j]);
}
}
}
}
return ans[len-1];
};
回溯
var letterCombinations = function(digits) {
const ans = [];
let s = [];
if(!digits) return ans;
const letterMap = ['', '', 'abc', 'def', 'ghi', 'jkl', 'mno', 'pqrs', 'tuv', 'wxyz'];
// index记录遍历到digits的第几位了
var backtracing = (digits, index) => {
if(digits.length === index) {
ans.push(s.join(''));
return;
}
let digit = digits[index];
let letter = letterMap[digit];
for(let i = 0; i < letter.length; i++) {
s.push(letter[i]);
backtracing(digits, index + 1);
s.pop(letter[i]);
}
}
backtracing(digits, 0);
return ans;
};
4. 组合总和
39. 组合总和-中等
b站讲解
本题没有元素的数量限制,只有总和限制。所以终止条件为sum>=target。
重点:刚开始自己写,一直运行不正确,要么是没去重,要么是结果不全,看了视频讲解,发现递归时函数参数是for循环中的i,也就是backtracing(sum, i);。
var combinationSum = function(candidates, target) {
const ans = [], path = [];
candidates.sort((a, b) => a - b);
var backtracing = (sum, index) => {
if(sum == target) {
ans.push([...path]);
return;
}
if(sum > target) return;
for(let i = index; i < candidates.length; i++) {
if(candidates[i] <= target - sum) {
path.push(candidates[i]);
sum += candidates[i];
backtracing(sum, i);
sum -= candidates[i];
path.pop();
}else{
// 对数组排完序后,如果当前candidates[i]已经大于target - sum了,直接break
break;
}
}
}
backtracing(0, 0);
return ans;
};
5.组合总和 II
40. 组合总和 II-中等
b站视频讲解
重点:去重。视频里提到树层去重与树枝去重,本题关键在于树层去重。
不用userd数组
自己做的时候,想到了if(candidates[i] == candidates[i - 1]) continue;,但去重效果并不理想。
最后发现少了个限定条件i > index,这样才能保证是树层去重,而树枝内的重复元素则不受影响。
var combinationSum2 = function(candidates, target) {
const ans = [], path = [];
candidates.sort((a, b) => a - b);
var backtracing = (sum, index) => {
if(sum == target) {
ans.push([...path]);
return;
}
if(sum > target) return;
for(let i = index; i < candidates.length; i++) {
if(i > index && candidates[i] == candidates[i - 1]) continue;
if(candidates[i] <= target - sum) {
path.push(candidates[i]);
sum += candidates[i];
backtracing(sum, i + 1);
path.pop();
sum -= candidates[i];
}else{
break;
}
}
}
backtracing(0, 0);
return ans;
};
userd数组
思路:利用userd数组标记元素,记录该元素是否使用过。
var combinationSum2 = function(candidates, target) {
const ans = [], path = [];
let used = new Array(candidates.length).fill(false);
candidates.sort((a, b) => a - b);
const backtracing = (sum, index) => {
if(sum == target) {
ans.push([...path]);
return;
}
for(let i = index; i < candidates.length && sum < target; i++) {
if((i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) || candidates[i] > target - sum) continue;
path.push(candidates[i]);
sum += candidates[i];
used[i] = true;
backtracing(sum, i + 1);
path.pop();
sum -= candidates[i];
used[i] = false;
}
}
backtracing(0, 0);
return ans;
};
最后
以上就是平淡大山最近收集整理的关于leetcode每天5题-Day471.组合2.组合总和 III3. 电话号码的字母组合4. 组合总和5.组合总和 II的全部内容,更多相关leetcode每天5题-Day471.组合2.组合总和内容请搜索靠谱客的其他文章。








发表评论 取消回复