快速排序之——Hoare方法一实现

81 阅读 0 评论 54 点赞

我是靠谱客的博主复杂红牛，最近开发中收集的这篇文章主要介绍快速排序之——Hoare方法一实现，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

快速排序的定义：

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

Hoare方法动态图：

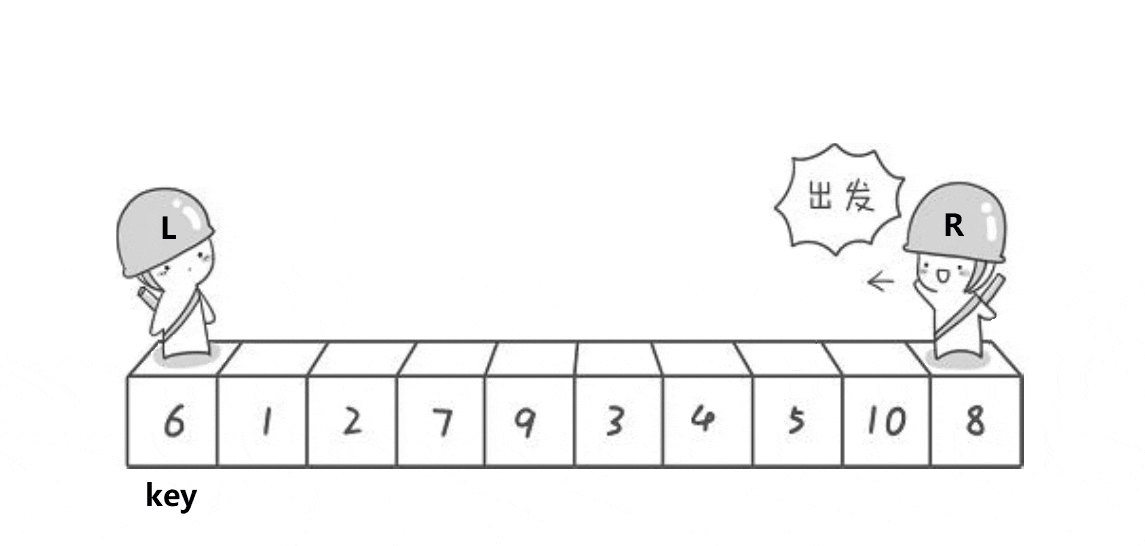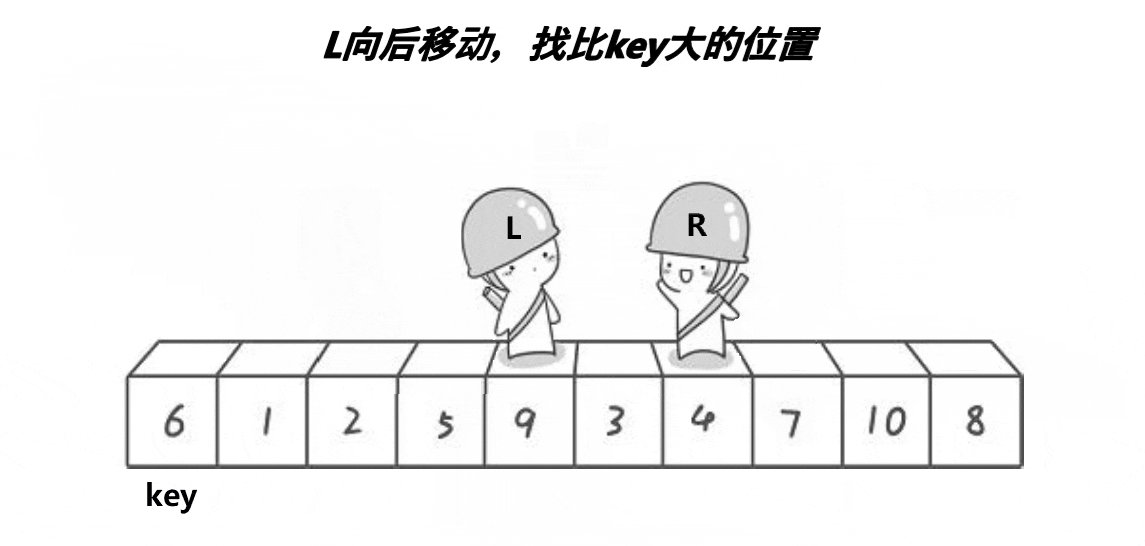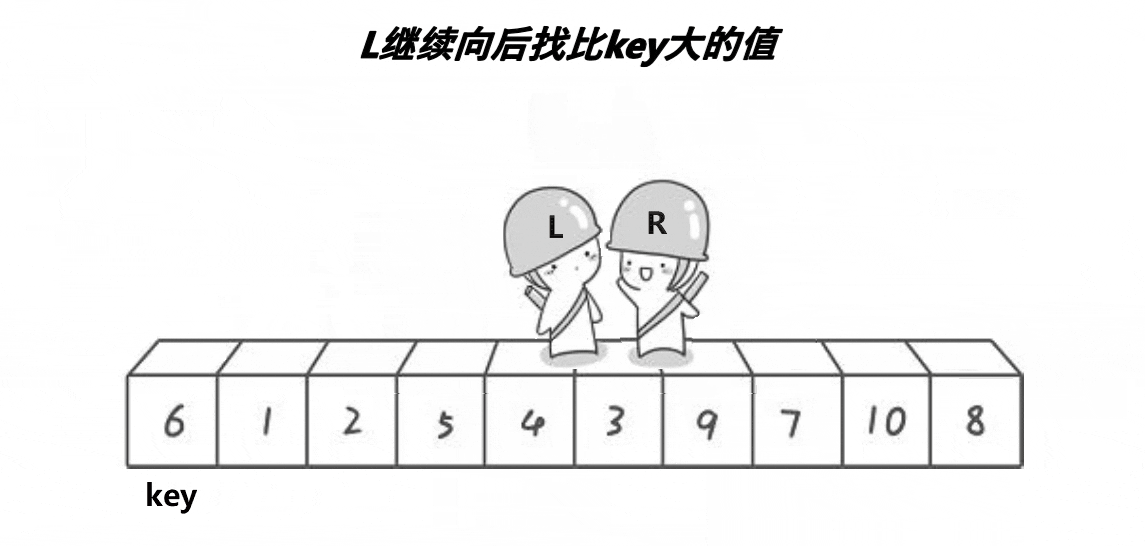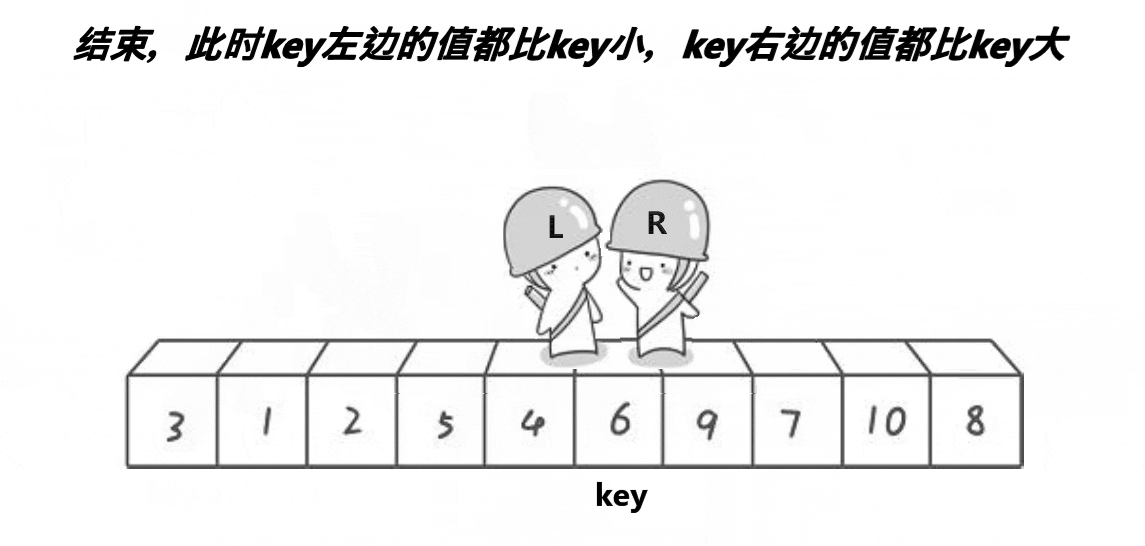
在动态图中，key称为基准值，默认把基准值定义在数组的首元素上，其次为了加快遍历的速度，需要用到两个变量分别去对应数组的首尾部分，L处在数列的首部，它需要从左往右寻找比Keyi位置的值大的，遇到后就停下来，没遇到就一直走；R处在数列的尾部，它需要从右往左去寻找比keyi位置的值小的，也是遇到后就停下来，没遇到就一直走。

当L与R都遇到停下来后开始互换位置，然后继续遍历，直到L==R时，双方都不会再走了，因为它们走到了同一个位置，这个位置被称为它俩的相遇点，之后便需要将keyi位置的值与相遇点的值互换位置，这样keyi位置的值就放到了中间，成为了数组的中心——基准值，它意味着将数组分为两个子序列，左序列全是小于Keyi的值，右序列全是大于Keyi的值，这样便可以利用递归，一层一层再对左右两个子序列进行相同的步骤——将一个大的无序序列转化为多个小的序列，从而进行排序，最终排列为完全有序的序列。

快速排序的步骤框架

// 假设按照升序对array数组中[left, right)区间中的元素进行排序
void QuickSort(int array[], int left, int right)
{
 if(right - left <= 1)
 return;
 
 // 按照基准值对array数组的 [left, right)区间中的元素进行划分
 int div = partion(array, left, right);
 
 // 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)
 // 递归排[left, div)
 QuickSort(array, left, div);
 
 // 递归排[div+1, right)
 QuickSort(array, div+1, right);
}

代码实现：

方法1：Hoare版本——快排递归

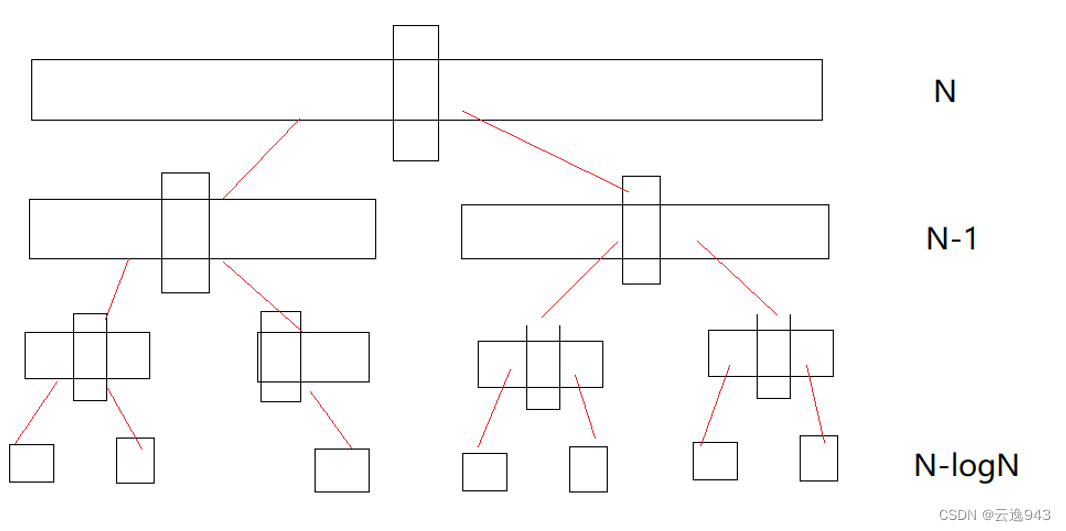
首先就是通过遍历将Key位置的值换到数组序列的中间部分，然后以Key为基准值，将序列递归分割，该方法的图解就像二叉树一样，所用的时间杂度为O(N*logN)，递归的层度为logN层。

int HoareSort(int* arr, int left, int right) {
	int keyi = left;
	while (left < right) {
		//注：在外层while中，left与right是不断变化的，
        //必须保证里层的while中的每一次循环都要符合
		// left<right,因为left可能有与right相遇或者错过的情况，
        //不允许有这种情况发生，否则会出错！！！
	
		//right先走
		while (left < right && arr[right] >= arr[keyi]) {
			--right;
		}
		//left再走
		while (left < right && arr[left] <= arr[keyi]) {
			++left;
		}

		//这时，left与right都找到了比Key...，跳出了循环，然后就开始互换
		if (left < right) {
			Swap(&arr[left], &arr[right]);
		}
		//互换完后再找，直到left>=right跳出大循环，
        //然后把left与right相遇点的位置与keyi互换即可
	}
	int meeti = left;
	Swap(&arr[meeti], &arr[keyi]);
	return meeti;
}

void QuickSort(int* arr, int left,int right) {
	if (left >= right) {
		return;
	}
	int keyi = HoareSort(arr, left, right);
	//递归，通过确定keyi的最终位置，将整个数组从中间分开，
    //keyi左边的为一组,keyi右边的为另一组
	//左边一组继续通过HoareSort进行寻找，排序。。。
    //右边也是如此，最后形成完整的有序数组
	QuickSort(arr, left, keyi - 1);
	QuickSort(arr, keyi + 1, right);
}

这种快排方法对于无序杂乱的序列来说，效率非常高，而对于接近有序和完全有序的数组序列，使用它效率就很低，它的时间复杂度会从O(N*logN)退化到O(N^2)，快排的效率就相当于冒泡排序，所以需要对Hoare方法进行相应的优化，使得快排对于任何类型的序列都能达到极高的效率！

优化方法1：三数取中

三数取中的思路：当我们知道数组的首部元素和尾部元素后，便可求出这个序列中间位置的数，我们只需要在首中尾这三个数中，挑出一个不是最大，也不是最小的中值，进行快速排序，便可加快提高快速排序效率。

为什么要取中值？假设待待排序的数列是一组高度有序的数列，显然数列首部很可能是极小值，数组的尾部是极大值，若选取一个排在中间的值，即使在最坏的情况下，right从右往左走，left从左往右走，right与left只需要走到中间位置便可以相遇，而这个数也正好是整个序列的均值。大大提高了快排效率。使用三数取中法消除了预排输入不好的情况，并且减少了快排大约14%的比较次数。

//算法优化法1.三数取中
int GetMidIndex(int* a, int left, int right) {
	int mid = (right - left) / 2;
	if (a[left] < a[mid]) {

		if (a[mid] < a[right])
			return mid;
		else if (a[left] > a[right])
			return left;
		else {
			return right;
		}
	}

	else {		                //a[left]>=a[mid]
		if (a[mid] > a[right])
			return mid;
		else if (a[left] < a[right])
			return left;
		else {
			return right;
		}
	}
}

int HoareSort(int* arr, int left, int right) {
	int mid = GetMidIndex(arr, left, right);
	Swap(&arr[left], &arr[mid]);
	int keyi = left;
	while (left < right) {
		

		//right先走
		while (left < right && arr[right] >= arr[keyi]) {
			--right;
		}
		//left再走
		while (left < right && arr[left] <= arr[keyi]) {
			++left;
		}

		//这时，left与right都找到了比Key...，跳出了循环，然后就开始互换
		if (left < right) {
			Swap(&arr[left], &arr[right]);
		}
		
	}
	int meeti = left;
	Swap(&arr[meeti], &arr[keyi]);
	return meeti;
}

void QuickSort(int* arr, int left, int right) {
	if (left >= right) {
		return;
	}

	int keyi = HoareSort(arr, left, right);
	QuickSort(arr, left, keyi - 1);
	QuickSort(arr, keyi + 1, right);
}

优化方法2：小区间优化法

小区间优化主要是针对快速排序的递归版本，其思想是如果某一趟区间的长度小于某一长度则不需要继续进行递归快排，而是使用其他排序将该区间的元素排序好。

//算法优化法2：小区间优化法

int HoareSort(int* arr, int left, int right) {
	int keyi = left;
	while (left < right) {
		//注：在外层while中，left与right是不断变化的，必须保证里层的while中的每一次循环都要符合
		// left<right,因为left可能有与right相遇或者错过的情况，不允许有这种情况发生，否则会出错！！！
	
		//right先走
		while (left < right && arr[right] >= arr[keyi]) {
			--right;
		}
		//left再走
		while (left < right && arr[left] <= arr[keyi]) {
			++left;
		}

		//这时，left与right都找到了比Key...，跳出了循环，然后就开始互换
		if (left < right) {
			Swap(&arr[left], &arr[right]);
		}
		//互换完后再找，直到left>=right跳出大循环，然后把left与right相遇点的位置与keyi互换即可
	}
	int meeti = left;
	Swap(&arr[meeti], &arr[keyi]);
	return meeti;
}

void QuickSort(int* arr, int left,int right) {
	if (left >= right) {
		return;
	}
	//当区间的长度小于等于某一长度时，使用直接插入算法进行排序，若还是使用递归快排，有些小题大做，杀鸡焉用牛刀了
	//因为小区间的的递归快排次数很少，递归又是那种浪费栈区空间，若是递归的多了，会栈溢出，所以能得话，就少递归
	if (right - left <= 8) {
		InsertSort(arr, right - left + 1);
	}

	//对于大于某一长度的区间长度，则还是使用递归快排
	else {
		int keyi = HoareSort(arr, left, right);
		//递归，通过确定keyi的最终位置，将整个数组从中间分开，keyi左边的为一组,keyi右边的为另一组
		//左边一组继续通过HoareSort进行寻找，排序。。。右边也是如此，最后形成完整的有序数组
		QuickSort(arr, left, keyi - 1);
		QuickSort(arr, keyi + 1, right);
	}
}