最小二乘法的实现

根据参考链接中的原理给出如下公式：

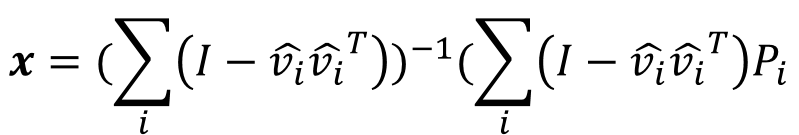
$x$为拟合结果。
代码如下：

import numpy as np
import math

def Intersection(LineD, PList):
	l = len(LineD)
	I = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
	q = np.array([0, 0, 0])
	Msum = np.array([[0, 0, 0], [0, 0, 0], [0, 0, 0]])
	
	for j in range(0,l):
		Lnormal = np.array([-LineD[l]/np.linalg.norm(LineD[l])])
		p = PList[l][:3]
		viviT = Lnormal*Lnormal.T
		M = I - viviT
		Msum = Msum + M
		q = q + np.dot(M,p)
	q = q.T
	lp = np.linalg.lstsq(Msum, q, rcond=None)[0]
	return lp

其中，输入的LineD为直线方向的List，格式为：[[x1,y1,z1], [x2,y2,z2],....]，P为直线上一点的坐标，格式与LineD相同。输出的lp为三维坐标。

Ransac优化

Ransac原理见链接。
主要实现步骤有：

• 随机抽取num条直线
• 最小二乘法算该组直线交点
• 计算距离交点在阈值t以内的直线个数count
• 重复抽取计算步骤n次，并选择所有结果中count最大时的交点并返回
• 为了使结果鲁棒，对所得结果内符合阈值条件内的直线再次计算交点，并与原结果比较，直到结果不再变化为止

代码如下：

import numpy as np
import math
import random

def RansacIntersection(LineD, PList, n, num, t):
    # LineD is the list of Light Direction
    # PList is the list of P position
    # n : times of sampling
    # num: number of lines during a sampling
    # t: threshold of distance to examine the number of lines around the point (unit: mm)

    l = len(LineD)
    I = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
    maxlines = 0
    reallp = []

    for i in range(0,n):
        #   pick up num line randomly
        #   calculate the intersection point
        #   calculate the distance between the point and lines
        #   count the number of lines around the point

        q = np.array([0, 0, 0])
        Msum = np.array([[0, 0, 0], [0, 0, 0], [0, 0, 0]])
        flag = random.sample(range(l), num)

        for j in range(0,num):
            flagj = flag[j]
            Lnormal = np.array([-LineD[flagj]/np.linalg.norm(LineD[flagj])])
            p = PList[flagj][:3]
            viviT = Lnormal*Lnormal.T
            M = I - viviT
            Msum = Msum + M
            q = q + np.dot(M,p)
        q = q.T
        lp = np.linalg.lstsq(Msum, q, rcond=None)[0]
        count = 0

        for j in range(0, l):
            Lnormal = np.array(-LineD[j] / np.linalg.norm(LineD[j]))
            p = PList[j][:3]
            P2L = np.array(lp - p)
            d = np.sqrt(1-(np.dot(Lnormal, P2L)/np.linalg.norm(P2L))**2)*np.linalg.norm(P2L)
            # print 1-(np.dot(Lnormal, P2L)/np.linalg.norm(P2L))**2
            # print d
            if d < t:
                count = count + 1
            # print count
            # print "****"
        if count > maxlines:
            maxlines = count
            reallp = lp

    lp0 = [[],[],[]]
    lp = reallp
    # print lp
    # print lp[0], lp[1], lp[2]
    while (not((lp0[0] == lp[0]) and (lp0[1] == lp[1]) and (lp0[2] == lp[2]))):
        count = 0
        # print "@@@@@@"
        q = np.array([0, 0, 0])
        Msum = np.array([[0, 0, 0], [0, 0, 0], [0, 0, 0]])
        for j in range(0, l):
            Lnormal = np.array(-LineD[j] / np.linalg.norm(LineD[j]))
            p = PList[j][:3]
            P2L = np.array(lp - p)
            d = np.sqrt(1 - (np.dot(Lnormal, P2L) / np.linalg.norm(P2L)) ** 2) * np.linalg.norm(P2L)

            if d < t:
                # print "****"
                count = count+1
                Lnormal = np.array([-LineD[j] / np.linalg.norm(LineD[j])])
                p = PList[j][:3]
                viviT = Lnormal * Lnormal.T
                M = I - viviT
                Msum = Msum + M
                q = q + np.dot(M, p)
        q = q.T
        lp0 = lp
        lp = np.linalg.lstsq(Msum, q, rcond=None)[0]
        # print lp

    reallp = lp
    print (count)

    # print "%%%%%"
    return reallp

第一次发博，不足之处请多多指教，如有问题欢迎讨论。

（转载请标明出处）

最后

以上就是热心帅哥为你收集整理的最小二乘法拟合直线簇交点及Ransac拟合最小二乘法的实现Ransac优化的全部内容，希望文章能够帮你解决最小二乘法拟合直线簇交点及Ransac拟合最小二乘法的实现Ransac优化所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。