MATLAB编写一段施密特正交的函数，输入为列向量，输出将矩阵每一列向量Schmidt正交化后的向量组

       最近帮人写一个施密特正交的程序，学习过线性代数或这数值计算时都会了解到施密特正交化方法，施密特正交是求欧式空间正交基的一种方法（事实上，在代数学中施密特正交也可拓展到一般的线性空间），即任意一组线性无关的向量，通过施密特正交化方法后得到的新的向量组中的向量两辆正交，且施密特正交化后的向量组与原向量组等价。

       施密特正交化的过程随处都可以找到，这里简单呈现一下，即α1，α2，α3...为一组线性无关的向量组，则可以通过施密特正交化的方法将其变为两两正交的向量组：

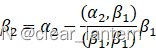
 以此类推，经过施密特正交化后的向量组β1，β2，β3...即为两两正交的正交组。

       现编写一个MATLAB函数，按照施密特正交化的方法，输入为矩阵，输出为将矩阵每一列作为一个向量，对该向量组进行施密特正交化得到的新的矩阵，以及每一列向量的模长（范数）。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function [Qhat,Rhat] = csg(A)

    [row,col]= size(A);
    Qhat = zeros(row,col);
    Rhat = zeros(1,col);
    
    Qhat(:,1)=A(:,1); 
    column1 = A(:,1);
    Rhat(1) = norm(column1);
    
    for j = 2 : col
        for i = 1: j-1            
            q(:,i) = ((Qhat(:,i)' * A(:,j))/(Qhat(:,i)' * Qhat(:,i)));
            r(:,j)= q(:,i) * Qhat(:,i);
            A(:,j)= A(:,j) -r(:,j);          
        end
        Qhat(:,j)=A(:,j);    
        Rhat(j)=norm(Qhat(:,j));
    end

若输入矩阵A为：

A =

     1     0     0
     1     1     0
     0     0     1

在命令行调用，[Qhat,Rhat] = csg(A)，运行结果为：

Qhat =

    1.0000   -0.5000         0
    1.0000    0.5000         0
         0         0    1.0000

Rhat =

    1.4142    0.7071    1.0000

其中Qhat为将A中每一列向量施密特正交化之后的组成的新的向量组。Rhat是Qhat中每一个列向量的模长，若想继续单位化操作即可直接坐商。

       代码中的方法即是常规的施密特正交化的方法，其中norm函数是matlab中自带的求范数的函数，norm(x,1)即是求向量x的1范数，若不给参数直接norm(x)默认求x的2范数，即欧式范数，也就是实域线性空间下向量的模长。

最后

以上就是轻松小懒猪最近收集整理的关于MATLAB编写一段施密特正交的函数，输入为列向量，输出将矩阵每一列向量Schmidt正交化后的向量组的全部内容，更多相关MATLAB编写一段施密特正交内容请搜索靠谱客的其他文章。