21天活动Zyf打卡第三天Promise9913，路径交叉

题目描述：

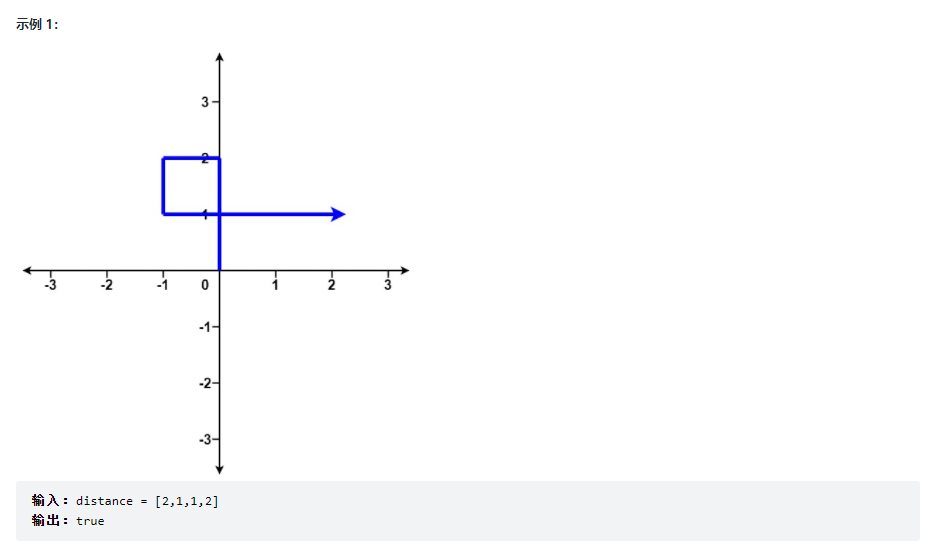
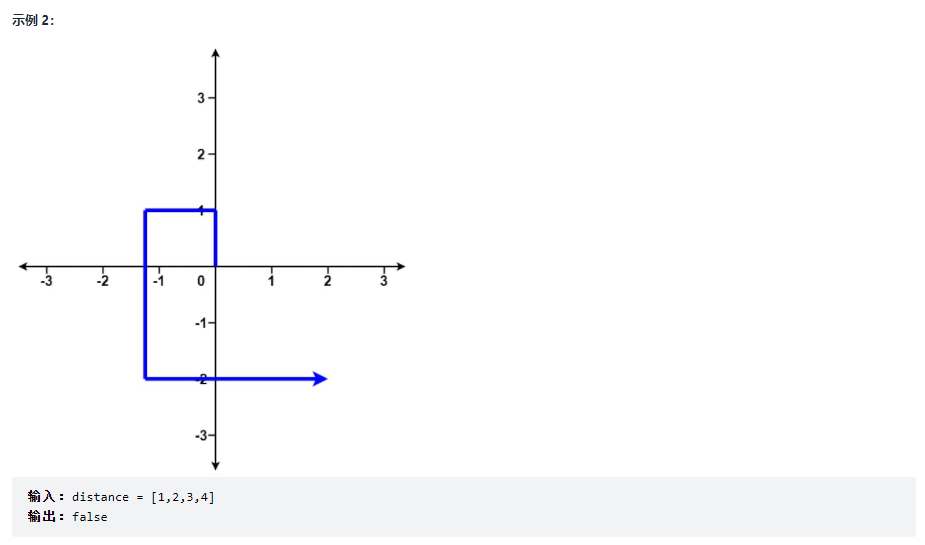
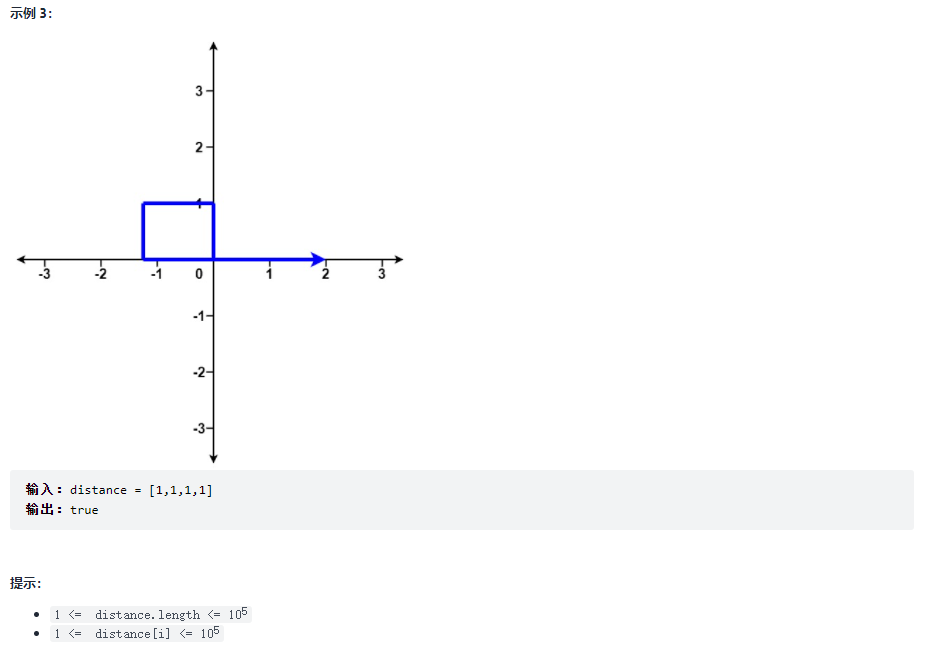
给你一个整数数组 distance 。

从 X-Y 平面上的点 (0,0) 开始，先向北移动 distance[0] 米，然后向西移动 distance[1] 米，向南移动 distance[2] 米，向东移动 distance[3] 米，持续移动。也就是说，每次移动后你的方位会发生逆时针变化。

判断你所经过的路径是否相交。如果相交，返回 true ；否则，返回 false 。

解题思路：

法一：归纳法（归纳路径交叉的情况）
思路和算法

根据归纳结果，我们发现所有可能的路径交叉的情况只有以下三类：

第 11 类，如上图所示，第 ii 次移动和第 i-3i−3 次移动（包含端点）交叉的情况，例如归纳中的 4-24−2、4-34−3、4-54−5 和 4-64−6。

这种路径交叉需满足以下条件：

第 i-1i−1 次移动距离小于等于第 i-3i−3 次移动距离。
第 ii 次移动距离大于等于第 i-2i−2 次移动距离。

第 22 类，如上图所示，第 55 次移动和第 11 次移动交叉（重叠）的情况，例如归纳中的 5-25−2 和 5-35−3。这类路径交叉的情况实际上是第 33 类路径交叉在边界条件下的一种特殊情况。

这种路径交叉需要满足以下条件：

第 44 次移动距离等于第 22 次移动距离。
第 55 次移动距离大于等于第 33 次移动距离减第 11 次移动距离的差；注意此时第 33 次移动距离一定大于第 11 次移动距离，否则在上一步就已经出现第 11 类路径交叉的情况了。

第 33 类，如上图所示，第 ii 次移动和第 i-5i−5 次移动（包含端点）交叉的情况，例如归纳中的 6-26−2 和 6-36−3。

这种路径交叉需满足以下条件：

第 i-1i−1 次移动距离大于等于第 i-3i−3 次移动距离减第 i-5i−5 次移动距离的差，且小于等于第 i-3i−3 次移动距离；注意此时第 i-3i−3 次移动距离一定大于第 i-5i−5 次移动距离，否则在两步之前就已经出现第 11 类路径交叉的情况了。
第 i-2i−2 次移动距离大于第 i-4i−4 次移动距离；注意此时第 i-2i−2 次移动距离一定不等于第 i-4i−4 次移动距离，否则在上一步就会出现第 33 类路径交叉（或第 22 类路径交叉）的情况了。
第 ii 次移动距离大于等于第 i-2i−2 次移动距离减第 i-4i−4 次移动距离的差。

class Solution:
    def isSelfCrossing(self, distance: List[int]) -> bool:
        n = len(distance)
        for i in range(3, n):
            # 第 1 类路径交叉的情况
            if (distance[i] >= distance[i - 2]
                    and distance[i - 1] <= distance[i - 3]):
                return True

            # 第 2 类路径交叉的情况
            if i == 4 and (distance[3] == distance[1]
                           and distance[4] >= distance[2] - distance[0]):
                return True

            # 第 3 类路径交叉的情况
            if i >= 5 and (distance[i - 3] - distance[i - 5] <= distance[i - 1] <= distance[i - 3]
                           and distance[i] >= distance[i - 2] - distance[i - 4]
                           and distance[i - 2] > distance[i - 4]):
                return True
        return False

复杂度分析

• 时间复杂度：O(n)O(n)，其中 nn 为移动次数。

• 空间复杂度：O(1)O(1)

最后

以上就是虚心跳跳糖为你收集整理的21天活动Zyf打卡第三天Promise9913，路径交叉的全部内容，希望文章能够帮你解决21天活动Zyf打卡第三天Promise9913，路径交叉所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。