概述
文章目录
- 直接结构
- 直接I型
- 直接II型
- 级联结构
- 并联结构
- 转置结构
一个数字滤波器在时域常用常系数线性差分方程表示
y
(
n
)
=
∑
k
=
0
M
b
k
x
(
n
−
k
)
−
∑
k
=
1
N
a
k
y
(
n
−
k
)
(1)
y(n)=sum_{k=0}^Mb_kx(n-k) - sum_{k=1}^N a_ky(n-k) tag{1}
y(n)=k=0∑Mbkx(n−k)−k=1∑Naky(n−k)(1)
不难得出其系统函数为
H
(
z
)
=
∑
k
=
0
M
b
k
z
−
k
1
+
∑
k
=
1
N
a
k
z
−
k
(2)
H(z) = frac{sum_{k=0}^M b_kz^{-k}}{1+sum_{k=1}^N a_kz^{-k}} tag{2}
H(z)=1+∑k=1Nakz−k∑k=0Mbkz−k(2)
无限长单位冲激响应(IIR)滤波器，其具有如下特点：
- 系统的单位抽样响应 h ( n ) h(n) h(n)是无限长的
- 从(1)中看，至少存在一个 a k ≠ 0 a_kneq 0 ak=0.也就是说输出到输入存在反馈,是递归结构
- 从(2)中看, H ( z ) H(z) H(z)在有限Z平面 ( 0 < ∣ z ∣ < ∞ ) (0<|z|<infty) (0<∣z∣<∞)一定存在极点.
- 单位冲激响应 h ( n ) h(n) h(n)为实数,则所有系数 ( a k , b k ) (a_k,b_k) (ak,bk)均为实数
直接结构
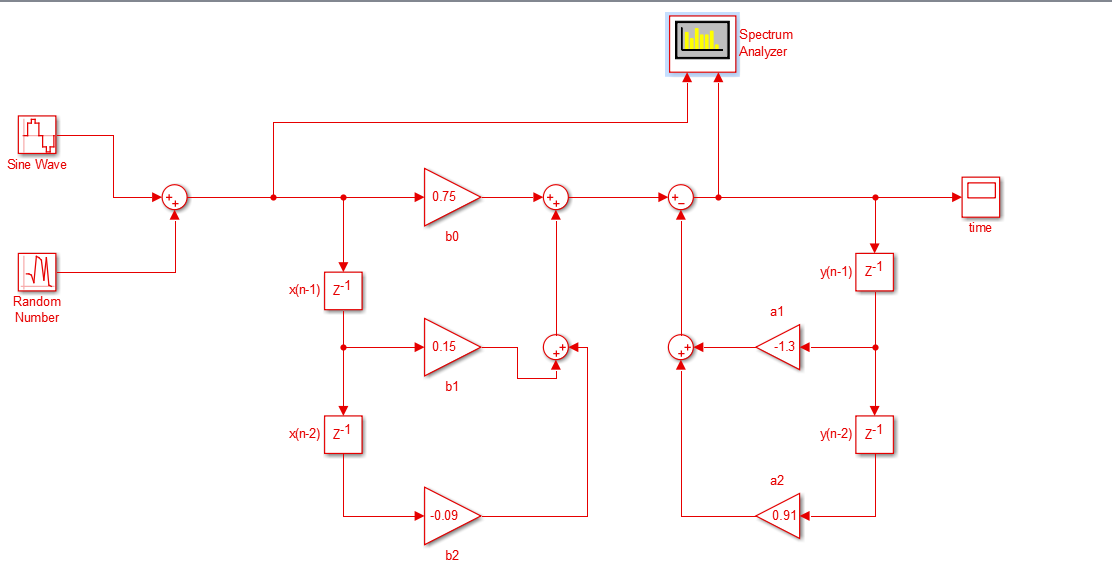
直接I型
根据时域表达式(1)首先将
x
(
n
−
k
)
x(n-k)
x(n−k)加权作和，再实现
y
(
n
−
k
)
y(n-k)
y(n−k)的加权和,就可以实现直接I型
直接II型
将I型中时延器合并，即可得到直接II型
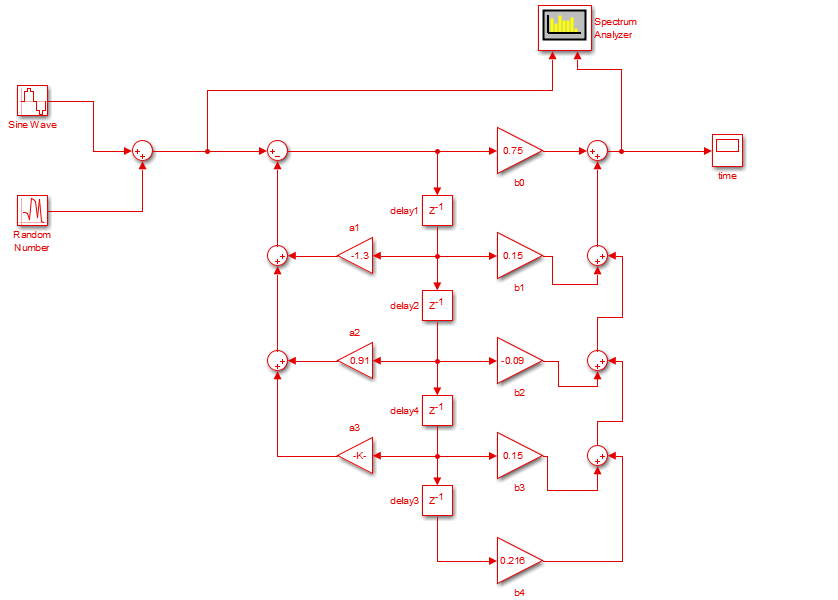
关于反馈网络的说明:
对于每一次 x ( n ) x(n) x(n)的输入,反馈网络不同于正馈网络1,仅运算一次输出.反馈网络的输出量将作为输入量继续影响反馈网络的输出，不断进行递归运算,直到全部反馈网络中不再产生输出量2,系统的响应才算结束.
级联结构
对系统函数表达式(2)进行因式分解，有
H
(
z
)
=
G
∏
j
=
1
m
(
1
−
ξ
i
z
−
1
)
∏
i
=
1
n
(
1
−
p
i
z
−
1
)
(3)
H(z)=G frac{prod_{j=1}^m (1-xi_i z^{-1})}{prod_{i=1}^n (1-p_i z^{-1})} tag{3}
H(z)=G∏i=1n(1−piz−1)∏j=1m(1−ξiz−1)(3)
将其中的共轭零极点合并
(
1
−
q
k
z
−
1
)
(
1
−
q
k
∗
z
−
1
)
=
1
−
(
q
k
+
q
k
∗
)
z
−
1
+
q
k
q
k
∗
z
−
2
(1-q_k z^{-1})(1-q_k^*z^{-1})=1-(q_k+q_k^*)z^{-1}+q_k q_k^* z^{-2}
(1−qkz−1)(1−qk∗z−1)=1−(qk+qk∗)z−1+qkqk∗z−2
系统函数将变为一阶与二阶因式相乘的形式,那么系统函数也可以进一步写为多个有理分式连乘的形式,其中每个可用如下通式表示
H
k
(
z
)
=
1
+
β
1
k
z
−
1
+
β
2
k
z
−
2
1
+
α
1
k
z
−
1
+
α
2
k
z
−
2
H_k(z)=frac{1+beta_{1k}z^{-1}+beta_{2k}z^{-2}}{1+alpha_{1k}z^{-1}+alpha_{2k}z^{-2}}
Hk(z)=1+α1kz−1+α2kz−21+β1kz−1+β2kz−2
频域相乘，时域卷积，所以滤波器的设计可以采用多个基本结构所代表的系统相连构成.
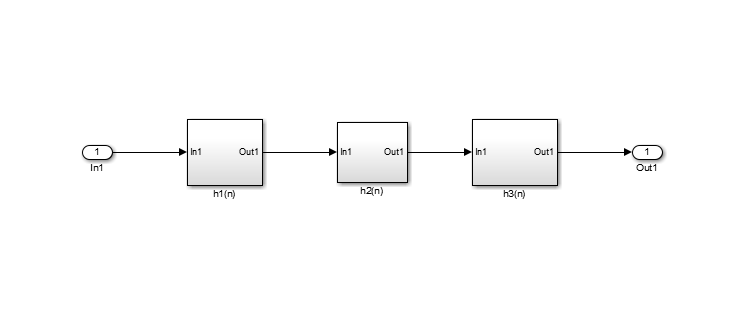
由于
H
(
z
)
=
Y
(
z
)
X
(
z
)
=
1
+
β
1
k
z
−
1
+
β
2
k
z
−
2
1
+
α
1
k
z
−
1
+
α
2
k
z
−
2
(4)
H(z)=frac{Y(z)}{X(z)}=frac{1+beta_{1k}z^{-1}+beta_{2k}z^{-2}}{1+alpha_{1k}z^{-1}+alpha_{2k}z^{-2}} tag{4}
H(z)=X(z)Y(z)=1+α1kz−1+α2kz−21+β1kz−1+β2kz−2(4)
对(4)进行逆Z变换，不难得出其对应网络的时域表达式
y
(
n
)
=
∑
k
=
0
2
β
k
x
(
n
−
k
)
−
∑
k
=
1
2
α
k
y
(
n
−
k
)
y(n)=sum_{k=0}^2beta_kx(n-k)-sum_{k=1}^2 alpha_k y(n-k)
y(n)=k=0∑2βkx(n−k)−k=1∑2αky(n−k)
一阶基本网络设计为
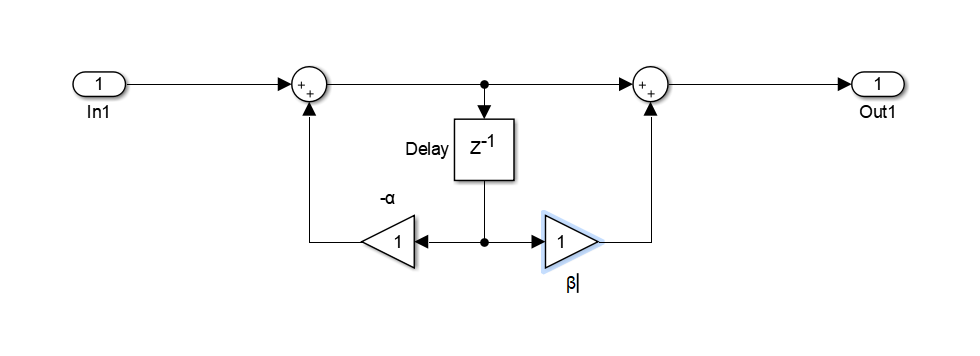
二阶基本网络设计
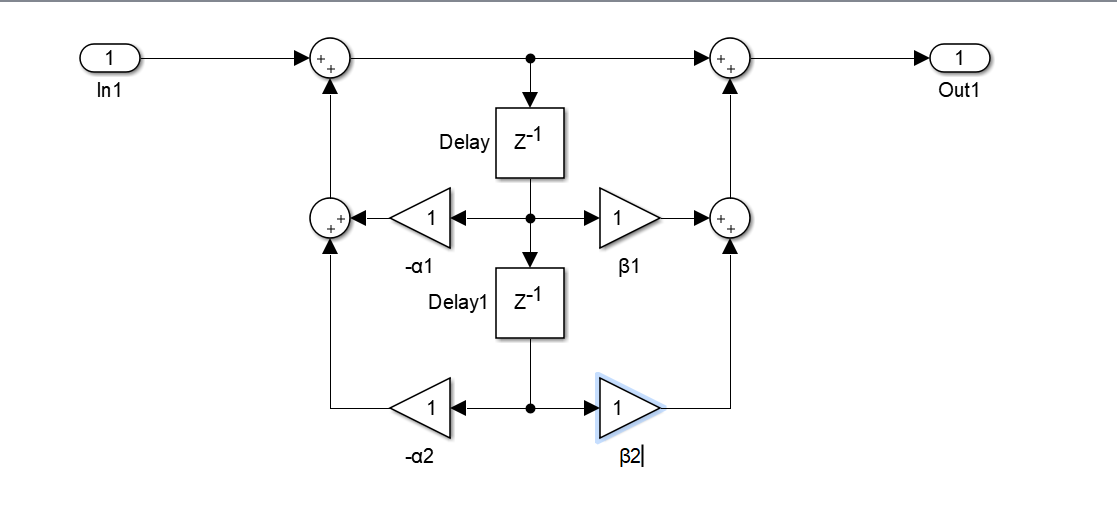需要注意的是
- 每级相连次序不唯一很灵活，但不同连接次序会有不同误差
- 联级网络间要有电平的放大与缩小
- 由于网络联级，误差会逐级累积
并联结构
将(3)进行部分分式展开
H
(
z
)
=
G
∑
i
=
0
N
A
i
1
−
p
i
z
−
1
+
∑
i
=
0
M
−
N
C
i
z
−
i
H(z)=Gsum_{i=0}^{N} frac{A_i}{1-p_iz^{-1}}+sum_{i=0}^{M-N} C_iz^{-i}
H(z)=Gi=0∑N1−piz−1Ai+i=0∑M−NCiz−i
在这里对展开式的第二部分进行说明:
- 当 M ≥ N Mgeq N M≥N时
分子可视为
n
u
m
e
r
a
t
o
r
=
P
1
⋅
d
e
n
o
m
i
n
a
t
o
r
+
P
2
numerator = P_1 cdot denominator +P_2
numerator=P1⋅denominator+P2
因此
C
i
C_i
Ci为
P
1
P_1
P1多项式各幂次系数,
P
2
P_2
P2留下为真分式的分母,进行部分展开.
- 当
M
<
N
M<N
M<N时
P 1 = 0 P_1=0 P1=0,此时H(z)为真分式,无额外常数项.
再将部分展开式的共轭极点合并,系统函数可以表示为
H
(
z
)
=
∑
i
=
0
N
B
0
k
+
B
1
k
z
−
1
1
+
A
1
k
z
−
1
+
A
2
k
z
−
2
+
∑
i
=
0
M
−
N
C
i
z
−
i
H(z)=sum_{i=0}^N frac{B_{0k}+B_{1k}z^{-1}}{1+A_{1k}z^{-1}+A_{2k}z^{-2}}+sum_{i=0}^{M-N} C_iz^{-i}
H(z)=i=0∑N1+A1kz−1+A2kz−2B0k+B1kz−1+i=0∑M−NCiz−i
将和式中每一部分作为一个基本结构,按照作和的关系并联连接
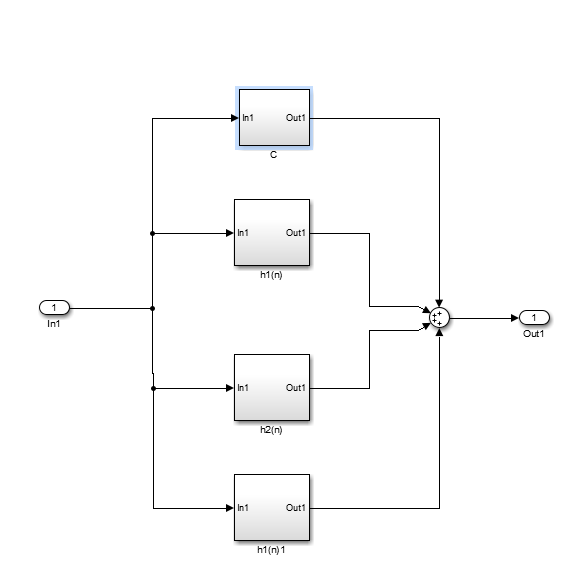
其中一、二阶基本网络与联级结构相同;常数部分设计如下
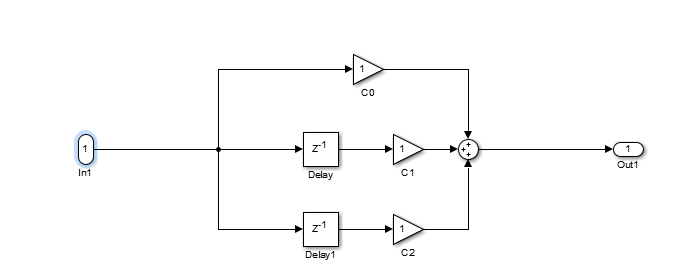相对于联级结构来说，并联结构各基本网络平行，因此所产生的误差不会累积，且信号同时加到各网络上，运算速度略快
转置结构
利用线性时不变系统的转置定理设计转置结构
对于线性时不变系统,将其流图的所有支路方向翻转,不改变支路增益,再交换输入输出位置，所得到新的网络为原网络的转置结构，二者系统函数相同
对 x ( n ) x(n) x(n)加权部分 ↩︎
多次时延后 y ( n − k ) = 0 y(n-k)=0 y(n−k)=0 ↩︎
最后
以上就是虚心跳跳糖为你收集整理的IIR基本结构直接结构级联结构并联结构转置结构的全部内容，希望文章能够帮你解决IIR基本结构直接结构级联结构并联结构转置结构所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复