当我们学习到离散时间非周期信号的傅里叶变换的时候，我们已经走到了频域分析的尾声。回顾之前所学，我们发现，其实连续时间和离散时间的傅里叶变换是有诸多相似之处的，但是两者之间却又有某些重大的不同。那么，下面我们就一起来看看 DTFT。

一、基本公式

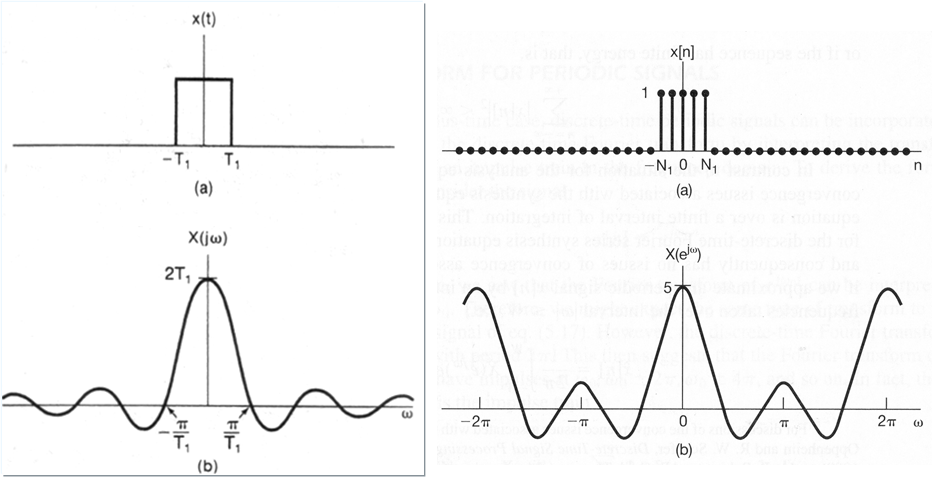
我们先回顾一下对于离散时间的周期方波，它的 DFS 是长什么样的：

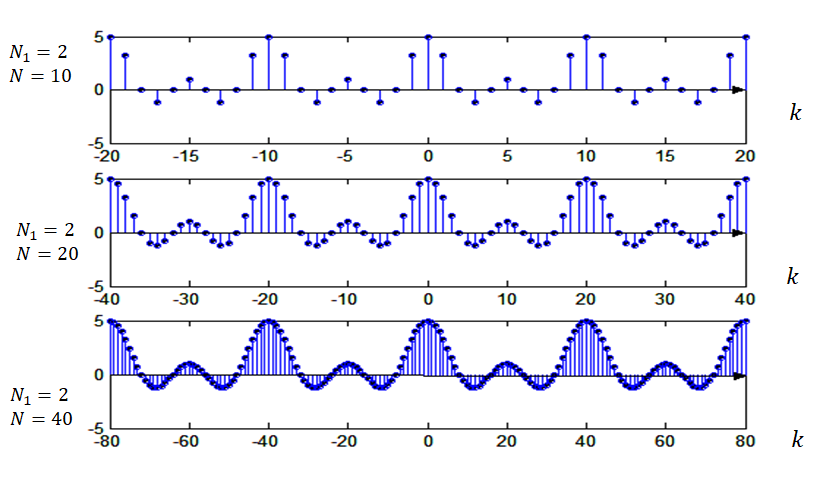
N 表示周期，N1 表示脉冲宽度。我们都可以看到，对于 DFS 而言，它是以 N 为周期的

当周期 N 趋于无穷时，周期信号就演变成了非周期信号。频谱也变成了上述 DFS 的包络。那么这就是傅里叶变换了。

离散时间非周期信号的傅里叶正变换：$$X(e^{j\omega })=\sum _{n-\infty }^{+\infty }x[n]e^{-j\omega n}$$
离散时间非周期信号傅里叶逆变换公式：$$x[n]=\frac{1}{2\pi }{\int }_{2\pi }X(e^{j\omega })e^{j\omega n}d\omega$$

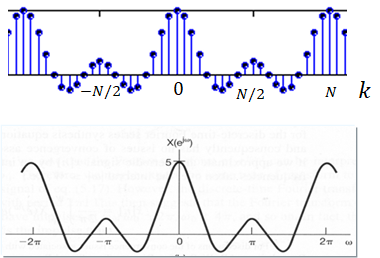
我们对比这两幅图，思考下面的一个问题：离散时间傅里叶变换得到的 $X(e^{j\omega })$ 是否具有周期性？
—— 答案是：YES！$X(e^{j\omega })$ 是以 $2\pi$ 为周期的。

二、离散时间傅里叶变换的收敛性

大家回顾一下，我们在上一篇 $Blog$ 里面说过：对于 DFS 来说，它是一定收敛的，所以不存在收敛条件的问题。但是对于 DTFT 而言，我们有下面两个条件，满足其中之一即可收敛：$$\begin{gathered} \sum _{n=-\infty }^{+\infty }|x[n]{|}^2<\infty \\ \sum _{n=-\infty }^{+\infty }|x[n]|<\infty \end{gathered}$$

三、常见信号的 DTFT

3.1 单边指数信号：$a^{n}u[n]$

它的频谱我们是必须要记住的：$$X(e^{j\omega })=\frac{1}{1-a{e}^{-j\omega }}$$
不过这里需要区别于连续时间的单边复指数信号 $e^{-at}u(t)$，它的频谱是：$X(j\omega )=\frac{1}{a+j\omega }$

对于这个 $X(e^{j\omega })=\frac{1}{1-a{e}^{-j\omega }}$ 我们还是有很多东西需要挖掘一下的：首先，这个频谱是一个复数，那么，我们需要从幅值和相角两个方面来讨论。其二、这个 $a$ 的取值也会使得频谱形状有较大的改变。

它的幅度我们可以表示为：$$|X(e^{j\omega })|=\frac{1}{\sqrt{1+a^2-2acos\omega }}$$
相位这里不再赘述，我们下面看看在 $0<a<1$ 的情况下的幅频特性和相频特性：

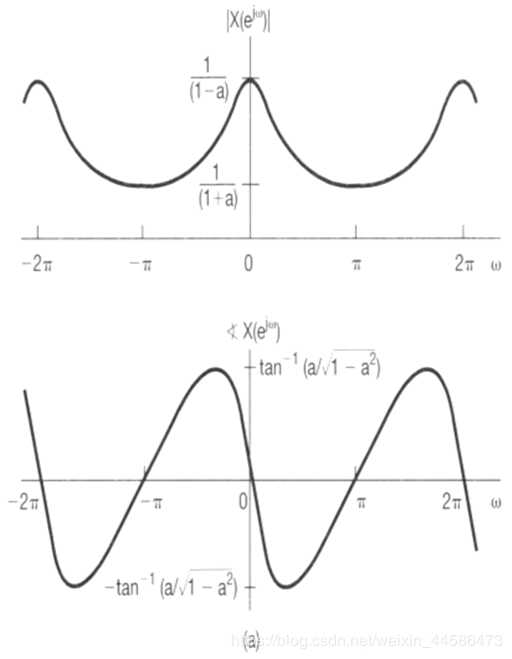
通过幅频特性曲线我们可以发现：该频谱在 频率为 $2k\pi$ 附近有较大的幅值，这就是所谓的低通滤波器（注意了：我们认为频率在 $2k\pi$ 附近的，都可以称之为低频成分），（频率在 $k\pi$ 附近的，可以称之为高频成分！）

下面，我们再看看当 $-1<a<0$ 时的频响：

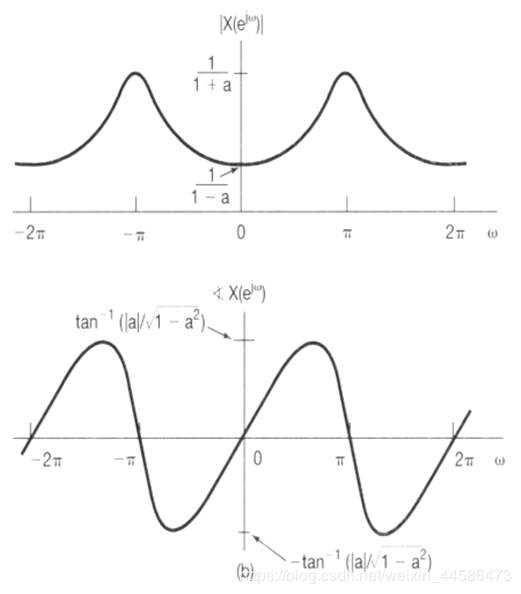
我们看到，只有在频率在 $k\pi$ 附近时，幅度才有较大的值，这就变成了高通滤波器！

3.2 单位冲激函数

单位冲激函数 $\delta [n]$ 的傅里叶变换就是幅度为 1 的直流信号

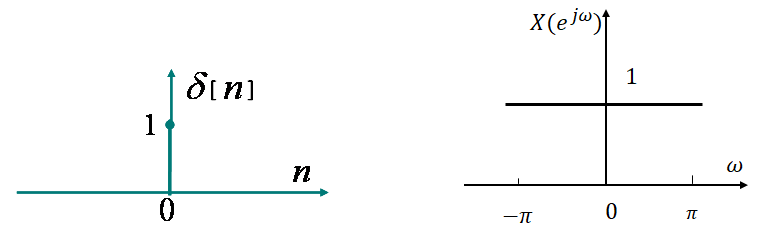
3.3 直流信号

$x[n]=1$ 的傅里叶变换为：${\sum }_{k=-\infty }^{+\infty }2\pi \delta (\omega -2k\pi )$

3.4 门信号

这个大家也不需要特别记忆，但是万一遇到了要会推导。（这里的推导还是需要一定的技巧的）
对于：$$x[n]=\{\begin{array}{l}1|n|\le N_1\\ 0|n|>N_1\end{array}$$
首先，我们直接上公式：$$\begin{array}{rl}X(e^{j\omega })& =\sum _{n=-\infty }^{+\infty }x[n]e^{-j\omega n}\\ & =\sum _{n=-N_1}^{+N_1}x[n]e^{-j\omega n}\end{array}$$
下面我们令：$m=n+N_1$，那么带入上式，就得到：$$\begin{array}{rl}X(e^{j\omega })& =\sum _{m=0}^{2N_1}{e}^{-j\omega (m-N_1)}(x[n]=1)\\ & =e^{j\omega N_1}\sum _{m=0}^{2N_1}{e}^{-j\omega m}\end{array}$$
对于：${\sum }_{m=0}^{2N_1}{e}^{-j\omega m}$ ，我们就可以看成是一个等比数列求和了：
因此，我们得到下面的一系列推导：

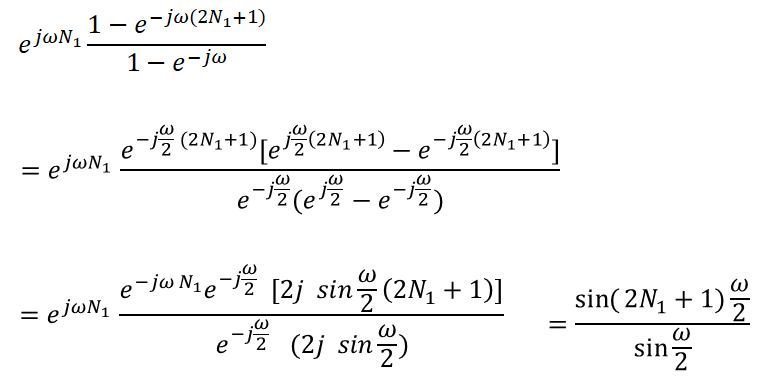
大家特别注意一下：提取因子的技巧（提取半频率）

3.5 离散时间周期信号的傅里叶变换

大家记住这个公式：$$X(e^{j\omega })=2\pi \sum _{k=-\infty }^{+\infty }{a}_k\delta (\omega -k\frac{2\pi }{N})$$

四、DTFT 有别于 CTFT 的几点性质

4.1 时域内插

我们知道，对于连续时间信号而言，假设把它做一定比例的压缩，再做一个拉伸，信号是能够恢复成原来的样子的。但是对于离散时间信号而言，对他的压缩相当于丢掉了一部分信息，那么此时再拉伸是无法变回去的。因此，下面我们看看对于离散时间信号而言，时域内插对 DTFT 有什么影响：

我们定义：$$x_{(k)}[n]=\{\begin{array}{l}x[\frac{n}{k}],n为k的整数倍时\\ 0,n不是k的整数倍时\end{array}$$

那么，当 k 是正数的时候，这样的操作就是相当于拉伸。那么我们记住：$$x_{(k)}[n]\underleftrightarrow{\mathcal{F}}X(e^{jk\omega })$$

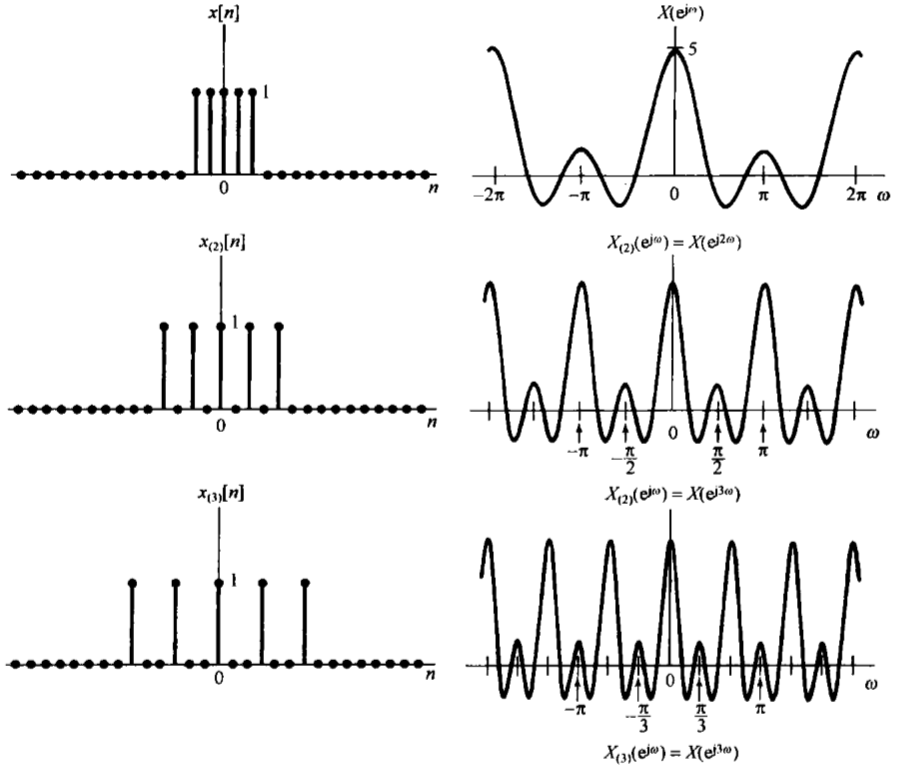
另外，还给了我们一个启发：时域扩展，对频谱而言就表现成压缩。

4.2 频域微分

注意是 “频域”，我们之前学习 CTFT 的时候讲的是时域微分。这里需要区分。我们下面直接给出i性质：$$\begin{gathered} x[n]\underleftrightarrow{\mathcal{F}}X(e^{j\omega }) \\ (-jn)x[n]\underleftrightarrow{\mathcal{F}}\frac{d(X(e^{j\omega }))}{d\omega } \end{gathered}$$

4.3 帕斯瓦尔定理

等式左边是时域信号的能量：$$\sum _{n=-\infty }^{+\infty }|x[n]{|}^2=\frac{1}{2\pi }{\int }_{2\pi }|X(e^{j\omega }){|}^{2}d\omega$$

至此，我们关于信号频域分析的系列 $Blog$ 就要告一段落啦！后面的 $Blog$ 将会重点聚焦滤波器、采样、通信系统、拉普拉斯变换等内容。see you！

最后

以上就是神勇玉米为你收集整理的【信号与系统学习笔记】—— 离散时间非周期信号的傅里叶变换 （DTFT)【概念+性质 一站式全解析】一、基本公式二、离散时间傅里叶变换的收敛性三、常见信号的 DTFT四、DTFT 有别于 CTFT 的几点性质的全部内容，希望文章能够帮你解决【信号与系统学习笔记】—— 离散时间非周期信号的傅里叶变换 （DTFT)【概念+性质 一站式全解析】一、基本公式二、离散时间傅里叶变换的收敛性三、常见信号的 DTFT四、DTFT 有别于 CTFT 的几点性质所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。