A题:
A题题目链接
题目描述:
Fibonacci-ish
Yash has recently learnt about the Fibonacci sequence and is very excited about it. He calls a sequence Fibonacci-ish if
- the sequence consists of at least two elements
- f0 and f1 are arbitrary
- fn + 2 = fn + 1 + fn for all n ≥ 0.
You are given some sequence of integers a1, a2, ..., an. Your task is rearrange elements of this sequence in such a way that its longest possible prefix is Fibonacci-ish sequence.
The first line of the input contains a single integer n (2 ≤ n ≤ 1000) — the length of the sequence ai.
The second line contains n integers a1, a2, ..., an (|ai| ≤ 109).
Print the length of the longest possible Fibonacci-ish prefix of the given sequence after rearrangement.
3
1 2 -1
3
5
28 35 7 14 21
4
NoteIn the first sample, if we rearrange elements of the sequence as - 1, 2, 1, the whole sequence ai would be Fibonacci-ish.
In the second sample, the optimal way to rearrange elements is
,
,
,
, 28.
题意:
给定一个长为n的序列,找出其中最长斐波那契子数列,并输出其长度。
解析:
这道题本来是想直接两个for循环暴力去做,然后利用"桶"的思想记录结果,看了下数据的范围|ai|<=10^9,显然用桶的思想是行不通的,然后想着是否能用二分查找,写了很久发现二分也不行,每次遍历叠加的过程中,每求得一次和就要找其后面的数是否有等于该数的,这样的话时间复杂度太大了,肯定是超时的,然后就在CSDN中查找别人的解题报告。发现大多数人的做法竟然还是两个for循环暴力求解,不过其中也做了很多优化,下面我就这题解说说自己的理解。
首先要明白的是斐波那契数列的组成,第一个和第二个数是指定的数,从第三个数开始,每个数都是其本身对应的前面两个数的和,那么我们就可以利用"桶"的思想,当将其中的两个数求和之后得到一个数,我们直接利用"桶"是否为0便可以判断该数是否存在,可是这道题数据范围达到了10^9,那么用数组作为"桶"显然是不行的,所以我们可以用map容器(映射关系),这也是一种类似于"桶"的容器,所以我们在输入数据的时候便可以先一一记录
每个数的个数,将这n个数进行升序排序。
"桶"的问题解决了,那么我们要怎么样找最长的斐波那契子序列呢?
根据以上对斐波那契数列的描述,我们每次最先要确定的是前两个数,那么再根据前两个数的和找第三个数,然后再根据第二第三个数的和找第四个数
....如此下去,直到第n个这样的数不存在。然后记录这次斐波那契子数列的长度。
以上描述的过程,是不是很像辗转相除法的过程呢?所以我们求最长子序列的长度则可以得出以下代码:
int find_quence(int a,int b)
{
int ans = 0;
if(f[a+b])
{
--f[a+b];
ans = find_quence(b,a+b) + 1;
++f[a+b];
}
return ans;
}该递归程序的解释:
首先递归程序我们要明确两个问题:
1.递归起始时的初始值
2.递归的终止条件.
很明显,这个递归程序的起始条件就是由主函数传上来的形参,终止条件就是f[a+b] = 0(map类容器f是我们的"桶")。一开始的时候,序列长度为0,
我们从第一次进入if循环开始分析,if循环成立,表示序列中有等于a+b的数存在,因此我们可以将该数并入序列中,所以要将该数出"桶",然后序列长
度加1之后,再按照同样的方式,寻找序列中第二个和第三个数的和是否存在。如此下去,当f[a+b]不存在时,即此时的f[a+b] = 0,那么if循环不成立,
函数返回0至上一层调用该函数的地方,后面的过程就类似于前缀和叠加的过程,一层一层的返回,将每次返回的结果一一的加到前面那个调用它的函
数的序列的长度上(其实这是一个回溯的过程,意思就是这条路径我已经探索完毕,我要回到我最初探索的地方,所以我探索过的地方都要一一的还回
去,以便我下一次再探索的时候使用),直到返回最初调用该函数的地方,将ans的结果带回主函数。
描述过程:
入栈 → 继续递归的条件不满足(停止入栈) -> 出栈(探索过的路径还回,将探索的结果报给自己的"上一级") -> 栈空 ->总的结果带回主函数
清楚以上过程之后,写出相应代码提交,可是却还是超时了。
原因在哪里呢?
斐波那契数列每一项都是不相同的,所以给定序列重复元素要预先处理掉,这样的话减少遍历次数,从而降低时间复杂度;
举个例子吧:
就像我们给出的样例1.
如果排序完的序列是这样的:
-1 -1 -1 -1 1 1 1 1 2 2 2 2 2
这样的序列最后的结果依旧是3,重复元素给我们的斐波那契数列的长度无任何贡献。但是遍历次数却多了。这样的序列本来遍历次数只要3*3.但是在
没有去重的情况下则变成了13*13,大量重复元素的情况下效率是非常低的。所以才会超时。这里的话调用了STL中的unique方法去重:
int N = unique(num,num+n) - num;
//去重,类似于剪枝的思想,减少重复计算的次数C++ STL算法系列4---unique , unique_copy函数
有了上面的几个优化之后,我们得出了这样的代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<map>
using namespace std;
const int maxn = 1010;
int num[maxn];
map<int,int> f;
int find_quence(int a,int b)
{
int ans = 0;
if(f[a+b])
{
--f[a+b];
ans = find_quence(b,a+b) + 1;
++f[a+b];
}
return ans;
}
int main()
{
int n;
scanf("%d",&n);
for(int i = 0;i < n;++i)
{
scanf("%d",&num[i]);
++f[num[i]];
}
sort(num,num+n);
//排序后减少重复遍历的次数
int ans = 0;
int N = unique(num,num+n) - num;
//去重,类似于剪枝的思想,减少重复计算的次数
for(int i = 0;i < N;++i)
for(int j = 0;j < N;++j)
{
if(i == j && f[num[i]]==1)
continue;
--f[num[i]],--f[num[j]];
ans = max(ans,find_quence(num[i],num[j]) + 2);
++f[num[i]],++f[num[j]];
}
printf("%dn",ans);
return 0;
}

可是,这并不是最优解,最优解耗时仅40+ms,有兴趣的可以研究研究:
codeforces 633D - Fibonacci-ish 离散化 + 二分查询
数据的离散化
B题:
B题题目链接
题目描述:
Print Check
Kris works in a large company "Blake Technologies". As a best engineer of the company he was assigned a task to develop a printer that will be able to print horizontal and vertical strips. First prototype is already built and Kris wants to tests it. He wants you to implement the program that checks the result of the printing.
Printer works with a rectangular sheet of paper of size n × m. Consider the list as a table consisting of n rows and mcolumns. Rows are numbered from top to bottom with integers from 1 to n, while columns are numbered from left to right with integers from 1 to m. Initially, all cells are painted in color 0.
Your program has to support two operations:
- Paint all cells in row ri in color ai;
- Paint all cells in column ci in color ai.
If during some operation i there is a cell that have already been painted, the color of this cell also changes to ai.
Your program has to print the resulting table after k operation.
The first line of the input contains three integers n, m and k (1 ≤ n, m ≤ 5000, n·m ≤ 100 000, 1 ≤ k ≤ 100 000) — the dimensions of the sheet and the number of operations, respectively.
Each of the next k lines contains the description of exactly one query:
- 1 ri ai (1 ≤ ri ≤ n, 1 ≤ ai ≤ 109), means that row ri is painted in color ai;
- 2 ci ai (1 ≤ ci ≤ m, 1 ≤ ai ≤ 109), means that column ci is painted in color ai.
Print n lines containing m integers each — the resulting table after all operations are applied.
3 3 3
1 1 3
2 2 1
1 2 2
3 1 3
2 2 2
0 1 0
5 3 5
1 1 1
1 3 1
1 5 1
2 1 1
2 3 1
1 1 1
1 0 1
1 1 1
1 0 1
1 1 1
NoteThe figure below shows all three operations for the first sample step by step. The cells that were painted on the corresponding step are marked gray.
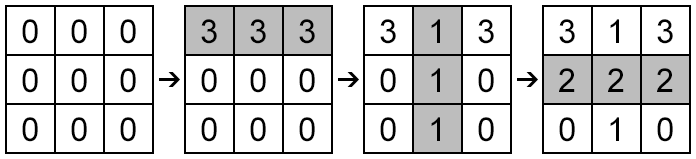
这道题其实不难,首先我们要看一下题目给出的数据范围:
n,m(1<n,m<=5000)分别是给定矩形的长和宽,并且n*m最大可达10^5,k为操作次数,达10^5次,但是题目限制时间只有1s,所以很明显如果我们
暴力去做的话,那么必然会超时。因此,我们应当对暴力的算法进行改进或者优化。
首先我们看操作类型和操作的过程是怎么样的,题设中给出两种:
1 ri ai(1表示操作的是"行",ri表示具体操作的是矩形的哪一行,ai表示将该行所有的数换成ai)
2 ci ai(2表示操作的是"列",ci表示具体操作的是矩形的哪一列,ai表示将该列所有的数换成ai)
最后输出在k次操作之后的矩形中所有的数(初始情况矩形中所有的数都是0)
那么我们需要思考的是,矩形中的数在k次操作之后最终变成的数字与什么有关?
为了解决这个疑问,我们可以看一下样例的解释,给定样例为:
3 3 3 1 1 3 2 2 1 1 2 2
首先我们是在第一行操作,将第一行所有的数字变成3,然后在第二列操作,将第二列所有的数字变成1,最后在第二行操作,将第
二行所有的数变成2,那么我们看图中,有哪些数被重复操作了?
有两个数,第一行的第二个,以及第二行的第二个,那么这两个数都变成什么数了?
第一行的第二个最后变成了1,而第二行的第二个最后变成了2.
那么这时候如果你还是觉得无规律可循的话,可以仿照以上方式,自己实现一下第二组测试样例
根据以上分析,其实我们可以发现,在n*m的矩形中,每个元素最后的值都取决于最后在该处操作的行或者是列
那么问题分析到这里,其实就很好解决了。对于每次输入的操作,我们只需要每次记录一下给出的行或者列操作的次序就好了,然
后在输出的时候,比较一下每个元素的所在行和所在列哪个操作是在最后(即标记的序号更大),如果该处没被操作过,那么输出0.
完整代码实现:
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = (int)1e5 + 10;
int kinds[maxn],pos[maxn],opr[maxn],row[5010],col[5010];
int main(){
int n,m,k;
scanf("%d %d %d",&n,&m,&k);
for(int i = 1;i <= k;++i){
scanf("%d %d %d",&kinds[i],&pos[i],&opr[i]);
if(kinds[i]==1){
row[pos[i]-1] = i;
}
else{
col[pos[i]-1] = i;
}
}
opr[0] = 0;
for(int i = 0;i < n;++i){
for(int j = 0;j < m;++j){
if(j == 0){
printf("%d",opr[max(row[i],col[j])]);
}
else{
printf(" %d",opr[max(row[i],col[j])]);
}
}
printf("n");
}
return 0;
}
C题:
C题题目链接
题目描述:
Watchmen
Watchmen are in a danger and Doctor Manhattan together with his friend Daniel Dreiberg should warn them as soon as possible. There are n watchmen on a plane, the i-th watchman is located at point (xi, yi).
They need to arrange a plan, but there are some difficulties on their way. As you know, Doctor Manhattan considers the distance between watchmen i and j to be |xi - xj| + |yi - yj|. Daniel, as an ordinary person, calculates the distance using the formula 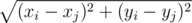 .
.
The success of the operation relies on the number of pairs (i, j) (1 ≤ i < j ≤ n), such that the distance between watchman iand watchmen j calculated by Doctor Manhattan is equal to the distance between them calculated by Daniel. You were asked to compute the number of such pairs.
The first line of the input contains the single integer n (1 ≤ n ≤ 200 000) — the number of watchmen.
Each of the following n lines contains two integers xi and yi (|xi|, |yi| ≤ 109).
Some positions may coincide.
Print the number of pairs of watchmen such that the distance between them calculated by Doctor Manhattan is equal to the distance calculated by Daniel.
3
1 1
7 5
1 5
2
6
0 0
0 1
0 2
-1 1
0 1
1 1
11
NoteIn the first sample, the distance between watchman 1 and watchman 2 is equal to |1 - 7| + |1 - 5| = 10 for Doctor Manhattan and
for Daniel. For pairs (1, 1), (1, 5) and (7, 5), (1, 5) Doctor Manhattan and Daniel will calculate the same distances.
题意不难理解,就是说给定n个点,找出其中满足 |xi - xj| + |yi - yj| = 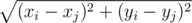
然后输出总对数即可(注意可能会有相同的点坐标)
首先我们看给定的这个条件,很自然我们便能想到就是将两边平方
然后将相同的项消去后,则得
|xi - xj| * |yi - yj| = 0.
那么要满足以上条件:
则必须满足 |xi - xj| = 0或者是|yi - yj| = 0.
即Xi = Xj或Yi = Yj;
然后这样就完了吗?注意这里还有个问题,题目中说了可能会有相同的点坐标,然后我们看示例2,不包括重复的点组成的满足题设的组,
我们计算得总共有10组,但是输出却是11,那么说明重复的点坐标也可以组成点坐标相同的组,但是涉及到了重复的点坐标组成点坐标相同的组
的问题,我们要考虑的是,该组中的点,X坐标和Y坐标都是相同的,所以我们在统计X坐标和Y坐标相同的组数时,都会将这些组记录进去。
所以这里就存在着重复记录的问题。
考虑完了以上问题之后,我们可以开始着手计算总的组数了,假如x值相等的组数为n1,y值相等的组数为n2
那么满足条件的总组数为ans = C(n1,2) + C(n2,2)
但是点坐标相同的组数我们重复计算了一次,所以我们应该再统计出点坐标相同的组数,然后再将总的组数减去重复记录的组数,即得最后的答案。
假设记录得重复的组数为k,那么最后的答案为:
ans = C(n1,2) + C(n2,2)- C(k,2)
完整代码实现:
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
typedef struct point Point;
typedef long long ll;
const int maxn = (int)2e5 + 10;
struct point{
ll x,y;
};
Point all[maxn];
ll pair_x[maxn],pair_y[maxn],repeat[maxn];
bool cmp1(Point a,Point b);
bool cmp2(Point a,Point b);
int main(){
int n;
while(scanf("%d",&n)==1&&n){
memset(pair_x,0,sizeof(pair_x));
memset(pair_y,0,sizeof(pair_y));
memset(repeat,0,sizeof(repeat));
for(int i = 0;i < n;++i){
scanf("%I64d %I64d",&all[i].x,&all[i].y);
}
sort(all,all+n,cmp1);
int k = 0;
for(int i = 0;i < n-1;++i){
if(all[i].x==all[i+1].x){
++pair_x[k];
}
else{
++k;
}
}
ll ans = 0;
for(int i = 0;i <= k;++i){
ans += pair_x[i]*(pair_x[i]+1) / 2;
}
sort(all,all+n,cmp2);
k = 0;
int flag = 0;
for(int i = 0;i < n-1;++i){
if(all[i].y==all[i+1].y){
++pair_y[k];
if(all[i].x==all[i+1].x){
//记录重复组数
++repeat[flag];
}
else{
++flag;
}
}
else{
++k;
++flag;
}
}
for(int i = 0;i <= flag;++i){
ans += pair_y[i]*(pair_y[i]+1) / 2;
}
for(int i = 0;i <= flag;++i){
ans -= repeat[i]*(repeat[i]+1) / 2;
}
printf("%I64dn",ans);
}
return 0;
}
//按x值升序排序,统计x值相等的组数
bool cmp1(Point a,Point b){
if(a.x==b.x){
return a.y < b.y;
}
else{
return a.x < b.x;
}
}
//按y值升序排序,统计y值相等的组数
bool cmp2(Point a,Point b){
if(a.y==b.y){
return a.x < b.x;
}
else{
return a.y < b.y;
}
}
而STL中的map类似于我们平常用的"桶"了(两元素之间的映射关系),然后使用pair作为map容器的第一个形参,记录重复组数。
C++ map的基本操作和使用
c++ 中 pair 的 使用方法
完整代码:
//来自codeforces
#include<cstdio>
#include<map>
#include<algorithm>
using namespace std;
typedef pair<int,int>P;
map<int,int>a,b;
map<P,int>c;
int n,i,x,y;
long long ans;
int main(){
scanf("%d",&n);
for(i=1;i<=n;i++){
scanf("%d%d",&x,&y);
ans+=a[x]+b[y]-c[P(x,y)];
//a[x],b[y],c[P(x,y)]分别是从0加至n-1
a[x]++;
b[y]++;
c[P(x,y)]++;
}
printf("%I64dn",ans);
return 0;
}
D题:
D题题目链接
题目描述:
Figure 1 shows a graphical representation of a binary tree of letters. People familiar with binary trees can skip over the Figure 1
definitions of a binary tree of letters, leaves of a binary tree, and a binary search tree of letters, and go right to The problem. A binary tree of letters may be one of two things:In the graphical representation of a binary tree of letters:
- It may be empty.
- It may have a root node. A node has a letter as data and refers to a left and a right subtree.
- The left and right subtrees are also binary trees of letters.
A leaf in a binary tree is a node whose subtrees are both empty. In the example in Figure 1,
- Empty trees are omitted completely.
- Each node is indicated by
- Its letter data,
- A line segment down to the left to the left subtree, if the left subtree is nonempty,
- A line segment down to the right to the right subtree, if the right subtree is nonempty.
this would be the five nodes with data B, D, H, P, and Y. The preorder traversal of a tree of letters satisfies the defining properties:The preorder traversal of the tree in Figure 1 is KGCBDHQMPY. A tree like the one in Figure 1 is also a binary search tree of letters.
- If the tree is empty, then the preorder traversal is empty.
- If the tree is not empty, then the preorder traversal consists of the following, in order
- The data from the root node,
- The preorder traversal of the root's left subtree,
- The preorder traversal of the root's right subtree.
A binary search tree of letters is a binary tree of letters in which each node satisfies: The root's data comes later in the alphabet than all the data in the nodes in the left subtree. The root's data comes earlier in the alphabet than all the data in the nodes in the right subtree. The problem: Consider the following sequence of operations on a binary search tree of letters Remove the leaves and list the data removed Repeat this procedure until the tree is empty Starting from the tree below on the left, we produce the sequence of trees shown, and then the empty treeby removing the leaves with data BDHPY CM GQ K Your problem is to start with such a sequence of lines of leaves from a binary search tree of letters and output the preorder traversal of the tree. 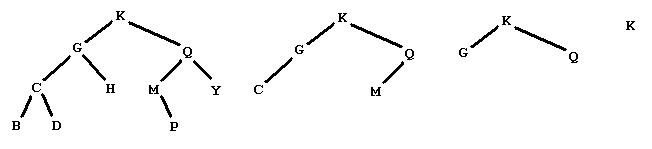
Input
The input will contain one or more data sets. Each data set is a sequence of one or more lines of capital letters. The lines contain the leaves removed from a binary search tree in the stages described above. The letters on a line will be listed in increasing alphabetical order. Data sets are separated by a line containing only an asterisk ('*'). The last data set is followed by a line containing only a dollar sign ('$'). There are no blanks or empty lines in the input.Output
For each input data set, there is a unique binary search tree that would produce the sequence of leaves. The output is a line containing only the preorder traversal of that tree, with no blanks.Sample Input
BDHPY CM GQ K * AC B $Sample Output
KGCBDHQMPY BAC题意:这道题题目实在是长....其实就是讲述二叉查找树的概念,然后给你一些字符串,这些字符串是从一棵完整的树上取下的。从第一次开始,每次获得的字符串都是树剩下部分的叶节点,当树空的时候停止。然后根据这些字符串,题设要求给出该树的先序遍历。解析:首先要明白二叉查找树的一些基本性质:二叉查找树(BinarySearch Tree,也叫二叉搜索树,或称二叉排序树Binary Sort Tree)或者是一棵空树,或者是具有下列性质的二叉树:
(1)、若它的左子树不为空,则左子树上所有结点的值均小于它的根结点的值;
(2)、若它的右子树不为空,则右子树上所有结点的值均大于它的根结点的值;
(3)、它的左、右子树也分别为二叉查找树。
根据上面题意的描述,我们很容易就能发现,最后一次揪下的叶节点必然就是根节点。所以,我们一开始就可以确定好根节点。然后由于每次获得的字符串都是树剩下部分的叶节点,所以我们可以推出:每次揪下的叶节点中,两两叶节点不成父子关系,并且子节点总是先于父节点被揪下。所以有了这样的推断,我们就可以将字符串从后往前进行"建树"。由于根节点已经确定,所以我们可以从倒数第二个字符串开始,从其第一个字符开始寻找它在树中的位置,一开始的时候是跟整棵树的根节点进行比较,如果该节点的值(即节点的数据域)小于根节点,则该节点必然位于根节点的左侧,然后查找的位置到了根节点的左孩子节点,反之则在根节点的右侧,当然,我们也需要另外声明一个Node类型的变量记住每次深入查找前当前节点的地址,这样的话方便后面找到待插入节点的位置时,将其插入树中,然后继续按照上述方式查找待插入节点的位置,直到当前查找到的位置为空,说明不能再继续查找了,那么此时该处便是待插入节点的位置。然后将待插入节点与其父节点进行比较,再将其插入树中即可。当整棵树建立起来之后,调用先序遍历函数输出其先序遍历即可。完整代码实现:#include<cstdio> #include<iostream> #include<algorithm> #include<string> using namespace std; typedef struct node Node; struct node{ //二叉树节点存储结构的定义 char data; Node *lchild,*rchild; }; Node *root = NULL; //表示整棵树的根节点 //节点初始化 Node *Init(Node *node,char _data){ node = (Node *)malloc(sizeof(Node)); node -> lchild = NULL; node -> rchild = NULL; node -> data = _data; return node; } //建树过程,即将每个节点插入其相应的位置 void build_tree(Node *node){ //printf("%c",node->data); Node *s = root; //从根节点开始寻找 Node *father; while(s){ father = s; if(s->data > node->data){ s = s -> lchild; //查找继续向左孩子节点深入 } else{ s = s -> rchild; //查找继续向右孩子节点深入 } } if(father->data > node->data){ father -> lchild = node; } else{ father -> rchild = node; } } //先序遍历 void preorder(Node *root){ if(root){ printf("%c",root->data); preorder(root -> lchild); preorder(root -> rchild); } } int main(){ string a[30]; int cnt; //记录字符串的数量 while(1){ cnt = 0; while(1){ getline(cin,a[cnt]); if(a[cnt]=="$" || a[cnt]=="*"){ break; } ++cnt; } root = Init(root,a[cnt-1][0]); //确定整棵树的根节点 int tmp = cnt; //暂存cnt的值 for(int i = tmp - 2;i >= 0;--i){ for(int j = 0;a[i][j] != '�';++j){ Node *p; p = Init(p,a[i][j]); //节点初始化 build_tree(p); //节点插入树中 } } preorder(root); printf("n"); if(a[cnt] == "*"){ continue; } else{ break; } } return 0; }
详解二叉查找树算法的实现E题:E题题目链接题目描述:Joysticks
TimeLimit:1000MS MemoryLimit:256MB64-bit integer IO format: %I64dProblem DescriptionFriends are going to play console. They have two joysticks and only one charger for them. Initially first joystick is charged at a1 percent and second one is charged at a2 percent. You can connect charger to a joystick only at the beginning of each minute. In one minute joystick either discharges by 2 percent (if not connected to a charger) or charges by 1 percent (if connected to a charger).
Game continues while both joysticks have a positive charge. Hence, if at the beginning of minute some joystick is charged by 1 percent, it has to be connected to a charger, otherwise the game stops. If some joystick completely discharges (its charge turns to 0), the game also stops.
Determine the maximum number of minutes that game can last. It is prohibited to pause the game, i. e. at each moment both joysticks should be enabled. It is allowed for joystick to be charged by more than 100 percent.
InputThe first line of the input contains two positive integers a1 and a2 (1 ≤ a1, a2 ≤ 100), the initial charge level of first and second joystick respectively.
OutputOutput the only integer, the maximum number of minutes that the game can last. Game continues until some joystick is discharged.
SampleInput 13 5SampleOutput 16SampleInput 24 4题意:SampleOutput 25NoteIn the first sample game lasts for 6 minute by using the following algorithm:
- at the beginning of the first minute connect first joystick to the charger, by the end of this minute first joystick is at 4%, second is at 3%;
- continue the game without changing charger, by the end of the second minute the first joystick is at 5%, second is at 1%;
- at the beginning of the third minute connect second joystick to the charger, after this minute the first joystick is at 3%, the second one is at 2%;
- continue the game without changing charger, by the end of the fourth minute first joystick is at 1%, second one is at 3%;
- at the beginning of the fifth minute connect first joystick to the charger, after this minute the first joystick is at 2%, the second one is at 1%;
- at the beginning of the sixth minute connect second joystick to the charger, after this minute the first joystick is at 0%, the second one is at 2%.
After that the first joystick is completely discharged and the game is stopped.
其实这道题是签到题,可是放在了E题的位置...两个游戏手柄都要充电,但只有一个充电器,不充电的情况下手柄每分钟会消耗2%的电,而充电的情况下每分钟会得到1%的电,不会同时充电和耗电,但是如果其中有手柄的电量到了1%,那么则该手柄一定要连接充电器。然后给出两个手柄的初始电量,求能持续的最长时间。解析:简单贪心,每次充电时优先给电量少的充电即可,但是要注意的是,当两个手柄的电量均为1%时,游戏也是要停止的(因为只有一个充电器),因此在考虑特殊情况后,得出以下完整代码:F题:#include<cstdio> int main(){ int a1,a2,ans = 0; scanf("%d %d",&a1,&a2); while(a1 > 0 && a2 > 0 && a1 + a2 > 2){ ans++; if(a1 > a2){ a1 -= 2; a2 += 1; } else{ a2 -= 2; a1 += 1; } } printf("%dn",ans); return 0; }F题题目链接题目描述:C. Spy Syndrome 2time limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard outputAfter observing the results of Spy Syndrome, Yash realised the errors of his ways. He now believes that a super spy such as Siddhant
can't use a cipher as basic and ancient as Caesar cipher. After many weeks of observation of Siddhant’s sentences,
Yash determined a new cipher technique.
For a given sentence, the cipher is processed as:
- Convert all letters of the sentence to lowercase.
- Reverse each of the words of the sentence individually.
- Remove all the spaces in the sentence.
For example, when this cipher is applied to the sentence
Kira is childish and he hates losing
the resulting string is
ariksihsidlihcdnaehsetahgnisol
Now Yash is given some ciphered string and a list of words. Help him to find out any original sentence composed using only words
from the list. Note, that any of the given words could be used in the sentence multiple times.
InputThe first line of the input contains a single integer n (1 ≤ n ≤ 10 000) — the length of the ciphered text.
The second line consists of nlowercase English letters — the ciphered text t.
The third line contains a single integer m (1 ≤ m ≤ 100 000) — the number of words
which will be considered while deciphering the text. Each of the next m lines contains a non-empty word wi (|wi| ≤ 1 000)
consisting of uppercase and lowercase English letters only. It's guaranteed that the total length of all words doesn't exceed 1 000 000.
OutputPrint one line — the original sentence. It is guaranteed that at least one solution exists. If there are multiple solutions, you may output any of those.
Examplesinput30 ariksihsidlihcdnaehsetahgnisol 10 Kira hates is he losing death childish L and NoteoutputKira is childish and he hates losinginput12 iherehtolleh 5 HI Ho there HeLLo hellooutputHI there HeLLoNoteIn sample case 2 there may be multiple accepted outputs, "HI there HeLLo" and "HI there hello" you may output any of them.
F题....并不会做....网上搜的解题报告都看不懂思路....太弱了.....
放两篇,你们有兴趣的可以去研究研究:
【Manthan, Codefest 16C】【DP SET-MAP 字典树哈希法】Spy Syndrome 2 字符串是否由字典库单词反转加密而成
Codeforces 633C Spy Syndrome 2 【字典树 + DFS】
官方解题报告(其中C对应周赛F,D对应周赛A)
总结:还是太弱了啊...得多充电涨姿势....
如有错误,还请指正,O(∩_∩)O谢谢
最后
以上就是粗心煎饼最近收集整理的关于第三周周赛——基础数据结构结业场(坚持就会有AK,题目出自codeforces 633C,633D,631B,651A,651C以及poj1577) Fibonacci-ish Print Check WatchmenJoysticks的全部内容,更多相关第三周周赛——基础数据结构结业场(坚持就会有AK,题目出自codeforces内容请搜索靠谱客的其他文章。






![[DFS] cf 134A Ice Skating](https://www.shuijiaxian.com/files_image/reation/bcimg9.png)


发表评论 取消回复