LIS(两种方法求最长上升子序列)

56 阅读 0 评论 37 点赞

我是靠谱客的博主寒冷苗条，最近开发中收集的这篇文章主要介绍LIS(两种方法求最长上升子序列)，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

首先得明白一个概念：子序列不一定是连续的，可以是断开的。

有两种写法：

一、动态规划写法

复杂度：O(n^2)

代码：

 1 #include <iostream>
 2 #include <queue>
 3 #include <cstdio>
 4 #include <algorithm>
 5 #include <cmath>
 6 #include <cstring>
 7 #define INF 0x3f3f3f3f
 8
 9 using namespace std;
10 typedef long long ll;
11 const int maxn = 1000;
12 int a[maxn],dp[maxn];
13
14 int main()
15 {
16
ios::sync_with_stdio(false);
17
int n;
18
while(cin>>n && n)
19 
{
20
for(int i = 0; i<n; i++)
21
cin>>a[i];
22
int mmax = -1;
23
for(int i = 0; i<n; i++)
24 
{
25
dp[i] = 1;
26
for(int j = 0; j<i; j++)//遍历之前的每一个元素pre
27 
{
28
if(a[j]<a[i] && (dp[j]+1>dp[i]))//如果元素pre < 当前元素cur,而且pre的长度+1要比当前的长度多就更新当前的长度
29 
{
30
dp[i] = dp[j]+1;
31 
}
32 
}
33
mmax = max(mmax,dp[i]);//维护最大的长度
34 
}
35
printf("%dn",mmax);
36 
}
37
return 0;
38 }

二、low_bound写法

复杂度：O(nlogn)

这种写法就是将动规写法中的第二层的遍历改为了二分查找。所以复杂度变为O(nlogn)

牛客讲解视频

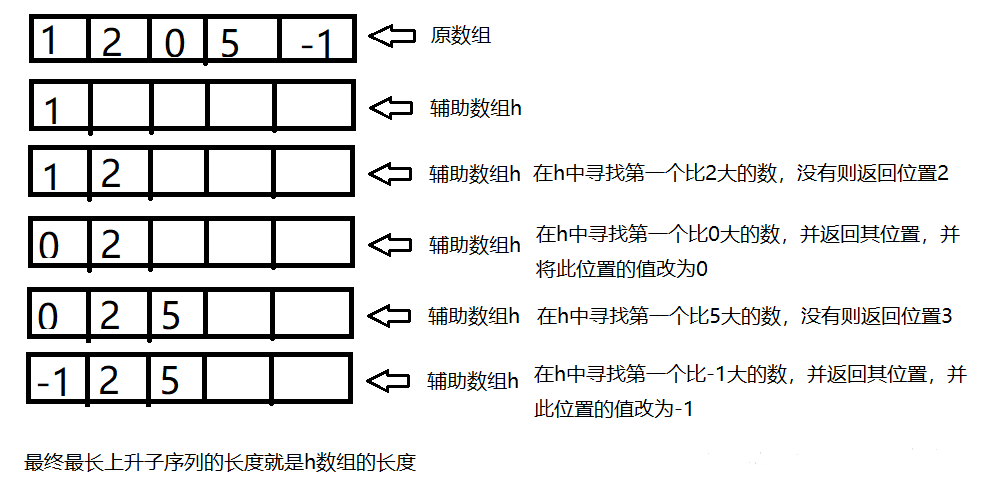
该算法中开了一个辅助数组h来表示该长度下最后的元素的最小值。例如 1、2、0、5 、-1

为什么要修改h数组里边的数为小的值呢，因为修改后h数组能变长的潜力就增大了，所以要修改。

代码：

 1 #include <iostream>
 2 #include <queue>
 3 #include <cstdio>
 4 #include <algorithm>
 5 #include <cmath>
 6 #include <cstring>
 7 #define INF 0x3f3f3f3f
 8
 9 using namespace std;
10 typedef long long ll;
11 const int maxn = 1000;
12 int a[maxn],dp[maxn];
13
14 int main()
15 {
16
ios::sync_with_stdio(false);
17
int n;
18
while(cin>>n)
19 
{
20
memset(a,0,sizeof(a));
21
for(int i = 0; i<n; i++)
22
dp[i] = INF;
23
for(int i = 0; i<n; i++)
24
cin>>a[i];
25
int mmax = -1;
26
for(int i = 0; i<n; i++)
27 
{
28
int k = lower_bound(dp, dp+n, a[i])-dp;
29
dp[k] = a[i];
30
mmax = max(mmax, k+1);
31 
}
32
printf("%dn",mmax);
33 
}
34
return 0;
35 }