1 内容简介

对AD芯片基本原理，分类与关键技术参数指标进行整理介绍。

2 模数转换

2.1 转换原理类别

AD转换就是模数转换。顾名思义，就是把模拟信号转换成数字信号。主要包括积分型、逐次逼近型、并行比较型/串并行型、Σ-Δ调制型、压频变换型。A/D转换器是用来通过一定的电路将模拟量转变为数字量。模拟量可以是电压、电流等电信号，也可以是压力、温度、湿度、位移、声音等非电信号。但在A/D转换前，输入到A/D转换器的输入信号必须经各种传感器把各种物理量转换成电压信号。

2.1.1 积分类型

一个积分型ADC是一种通过使用积分器将未知的输入电压转换成数字表示的一种模-数转换器。在它最基本的实现中，这个未知的输入电压是被施加在积分器的输入端，并且持续一个固定的时间段（所谓的上升阶段）。然后用一个已知的反向电压施加到积分器，这样持续到积分器输出归零（所谓的下降阶段）。这样，输入电压的计算结果实际是参考电压的一个函数，定时上升阶段时间和测得的下降阶段时间。下降阶段时间的测量通常是以转换器的时钟为单位，所以积分时间越长，分辨率越高。同样的，转换器的速度可以靠牺牲分辨率来获得提升。这种类型的AD转换器可以获得高分辨率，但是通常这样做会牺牲速度。因此，这些转换器不适用于音频或信号处理的场合应用。 他们通常的典型应用就是数字电压计和其他需要高精度测量的仪表。
如图2.1与图2.2所示，转换过程分两个阶段：上升阶段和下降阶段。在上升阶段，积分器的输入是被测电压，在下降阶段，积分器的输入是已知的参考电压。在上升阶段中，开关选择被测电压进入积分器，积分器持续一个固定的时间段进行积分，在积分电容上面积累电荷。在下降阶段，开关选择参考电压进入积分器，在这阶段测量积分器输入归零的时间。

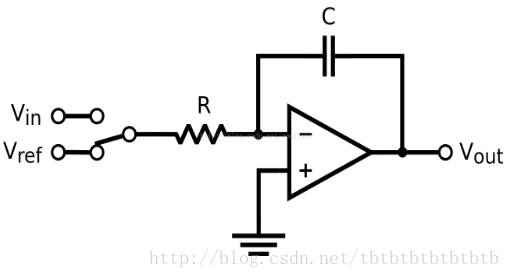
图2.1 ADC基本原理示意图

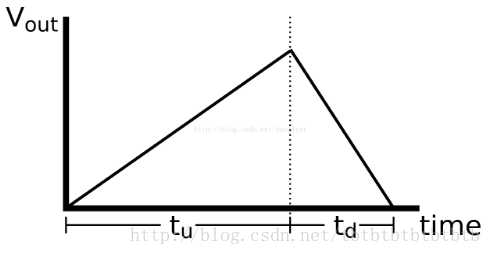
图2.2 采样电路充放电过程电压变化图示

2.1.2 逐次逼近类型

逐次逼近型adc由比较器、D/A转换器、缓冲寄存器和若干控制逻辑电路构成。原理是从高位到低位逐位比较，首先将缓冲寄存器各位清零；转换开始后，先将寄存器最高位置1，把值送入D/A转换器，经D/A转换后的模拟量送入比较器，称为 Vo，与比较器的待转换的模拟量Vi比较，若Vo

2.1.3 并行比较类型

一种典型的3位并行比较型A/D转换器原理电路如下图所示。它由电阻分压器、电压比较器、寄存器及编码器组成。
图中的8个电阻将参考电压VREF分成8个等级，其中7个等级的电压分别作为7个比较器 C1～C7 的参考电压，其数值分别为VREF/15、3VREF/15…、13VREF/15。输入电压为v1，它的大小决定各比较器的输出状态，如当0≤v1< VREF/15时，C7～C1的输出状态都为0；当3VREF/15≤v1<5VREF/15时，比较器C6和C7的输出CO6=CO7=1，其余各比较器的状态均为0。根据各比较器的参考电压值，可以确定输入模拟电压值与各比较器输出状态的关系。比较器的输出状态由D触发器存储，经优先编码器编码，得到数字量输出。优先编码器优先级别最高是I7 ，最低的是I1。设v1变化范围是 0～VREF，输出3位数字量为D2D1D0,3位并行比较型A/D转换器的输入、输出关系如图2.4所示所示。

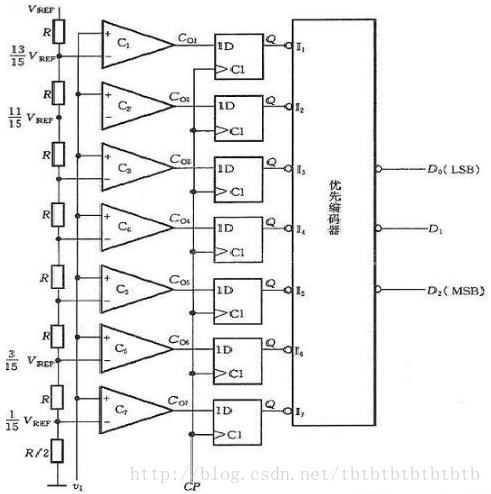
图2.3 三位并行比较ADC示意图

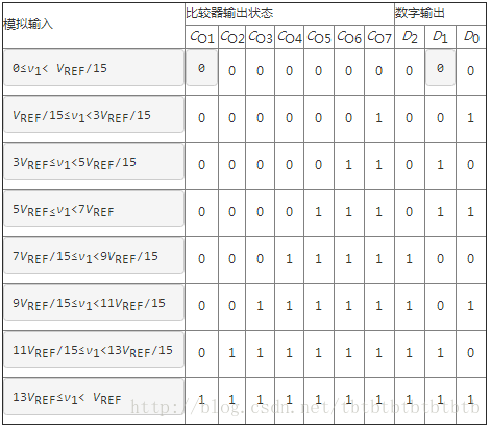
图2.4 三位并行比较ADC输出示意图

这类型芯片具有以下特点：
 由于转换是并行的，其转换时间只受比较器、触发器和编码电路延迟时间的限制，因此转换速度最快。
 随着分辨率的提高，元件数目要按几何级数增加。一个n位转换器，所用比较器的个数为2n-1，如8位的并行A/D转换器就需要28-1=255个比较器。由于位数愈多，电路愈复杂，因此制成分辨率较高的集成并行A/D转换器是比较困难的。
 精度取决于分压网络和比较电路。
 动态范围取决于VREF。

2.1.4 sigma类型

我们要解释∑-ΔADC的原理，这包含了几个基本理论：过采样(over sampling），量化噪声整形（quantization），数字滤波（digital filtering），抽取（decimation）。Σ-Δ转换器中的模拟部分非常简单（类似于一个1bit ADC），而数字部分要复杂得多，按照功能可划分为数字滤波和抽取单元。由于更接近于一个数字器件，Σ-ΔADC的制造成本非常低廉。
过采样：首先，考虑一个传统ADC的频域传输特性。输入一个正弦信号，然后以频率fs采样–按照 Nyquist定理，采样频率至少两倍于输入信号。从FFT分析结果可以看到，一个单音和一系列频率分布于DC到fs /2间的随机噪声。这就是所谓的量化噪声，主要是由于有限的ADC分辨率而造成的。单音信号的幅度和所有频率噪声的RMS幅度之和的比值就是信号噪声比（SNR）。对于一个Nbit ADC，SNR可由公式：SNR=6.02N+1.76dB得到。为了改善SNR和更为精确地再现输入信号，对于传统ADC来讲，必须增加位数。

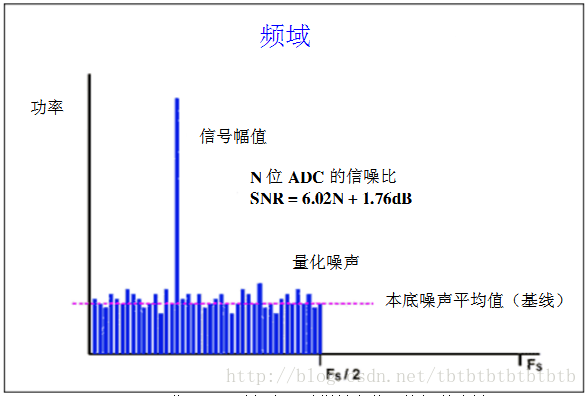
图 N位ADC以fs采样单频点信号频谱图

如果将采样频率提高一个过采样系数k，即采样频率为kfs，再来讨论同样的问题。FFT分析显示噪声基线降低了，SNR值未变，但噪声能量分散到一个更宽的频率范围。Σ-Δ转换器正是利用了这一原理，具体方法是紧接着1bit ADC之后进行数字滤波。大部分噪声被数字滤波器滤掉，这样，RMS噪声就降低了，从而一个低分辨率ADC，Σ-Δ转换器也可获得宽动态范围。

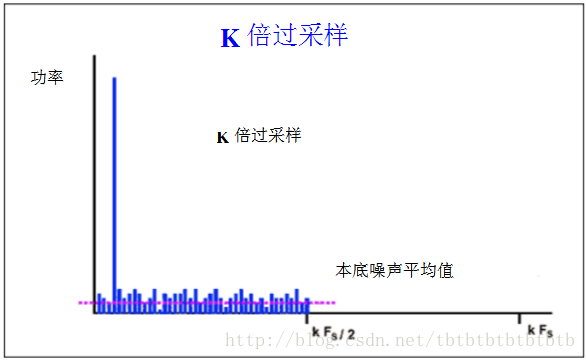
图 N位ADC以K*fs采样单频点信号频谱图

那么，简单的过采样和滤波是如何改善SNR的呢？一个1bit ADC的SNR为7.78dB（6.02+1.76），每4倍过采样将使SNR增加6dB，SNR每增加6dB等效于分辨率增加1bit。这样，采用1bit ADC进行64倍过采样就能获得4bit分辨率；而要获得16bit分辨率就必须进行415倍过采样，这是不切实际的。Σ-Δ转换器采用噪声成形技术消除了这种局限，每4倍过采样系数可增加高于6dB的信噪比。

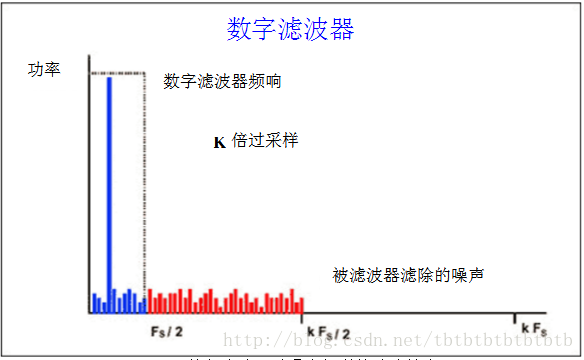
图 数字滤波器对噪声信号的减弱效果

量化噪声整形：Σ-Δ调制器包含1个差分放大器、1个积分器、1个比较器以及1个由1bit DAC（1个简单的开关，可以将差分放大器的反相输入接到正或负参考电压）构成的反馈环。反馈DAC的作用是使积分器的平均输出电压接近于比较器的参考电平。调制器输出中”1”的密度将正比于输入信号，如果输入电压上升，比较器必须产生更多数量的”1”，反之亦然。积分器用来对误差电压求和，对于输入信号表现为一个低通滤波器，而对于量化噪声则表现为高通滤波。这样，大部分量化噪声就被推向更高的频段。和前面的简单过采样相比，总的噪声功率没有改变，但噪声的分布发生了变化。

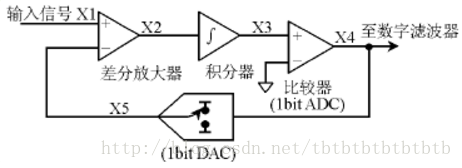
图 Σ-Δ调制器

现在，如果对噪声成形后的Σ-Δ调制器输出进行数字滤波，将有可能移走比简单过采样中更多的噪声。这种调制器（一阶）在每两倍的过采样率下可提供9dB的SNR改善。
在Σ-Δ调制器中采用更多的积分与求和环节，可以提供更高阶数的量化噪声成形。例如，一个二阶Σ-Δ调制器在每两倍的过采样率下可改善SNR 15dB。图2显示了Σ-Δ调制器的阶数、过采样率和能够获得的SNR三者之间的关系。

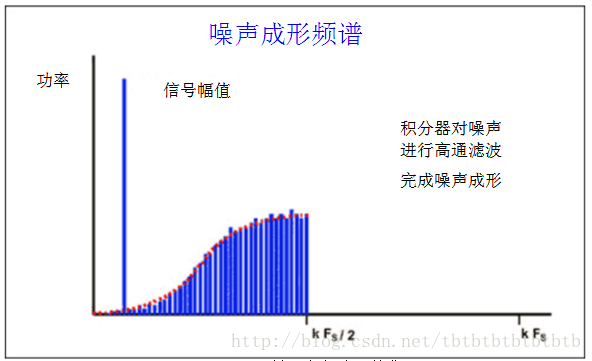
图 量化噪声整形示意图

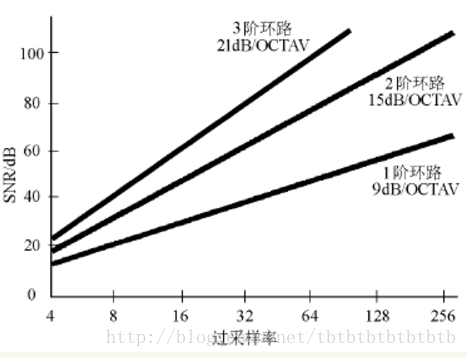
图 SNR与过采样率的关系

数字滤波：Σ-Δ调制器以采样速率输出1bit数据流，频率可高达MHz量级。数字滤波和抽取的目的是从该数据流中提取出有用的信息，并将数据速率降低到可用的水平。Σ-ΔADC中的数字滤波器对1bit数据流求平均，移去带外量化噪声并改善ADC的分辨率。数字滤波器决定了信号带宽、建立时间和阻带抑制。
抽取：由于带宽被输出数字滤波器降低，输出数据速率可低于原始采样速率，但仍满足Nyquist定律。这可通过保留某些采样而丢弃其余采样来实现，这个过程就是所谓的按M因子”抽取”。M因子为抽取比例，可以是任何整数值。在选择抽取因子时应该使输出数据速率高于两倍的信号带宽。这样，如果以fs的频率对输入信号采样，滤波后的输出数据速率可降低至fs /M，而不会丢失任何信息。

2.2 关键技术参数

2.2.1 分辨率

简单点说，“精度”是用来描述物理量的准确程度的，而“分辨率”是用来描述刻度划分的。从定义上看，这两个量应该是风马牛不相及的。简单做个比喻：有这么一把常见的塑料尺（中学生用的那种），它的量程是10厘米，上面有100个刻度，最小能读出1毫米的有效值。那么我们就说这把尺子的分辨率是1毫米，或者量程的1%；而它的实际精度就不得而知了（算是0.1毫米吧）。当我们用火来烤一下它，并且把它拉长一段，然后再考察一下它。我们不难发现，它还有有100个刻度，它的“分辨率”还是1毫米，跟原来一样！然而，您还会认为它的精度还是原来的0.1毫米么？

2.2.2 转换速率

转换速率(Conversion Rate)是指完成一次从模拟转换到数字的AD转换所需的时间的倒数。积分型AD的转换时间是毫秒级属低速AD，逐次比较型AD是微秒级属中速AD，全并行/串并行型AD可达到纳秒级。采样时间则是另外一个概念，是指两次转换的间隔。为了保证转换的正确完成，采样速率(Sample Rate)必须小于或等于转换速率。因此有人习惯上将转换速率在数值上等同于采样速率也是可以接受的。

2.2.3 精度与误差

常用的A/D转换器主要存在：失调误差、增益误差和线性误差。

2.2.3.1 基准误差

采用内部或外部基准的ADC的一个最大潜在误差源是参考电压。很多情况下，内置于芯片内部的基准通常都没有足够严格的规格。为了理解基准所带来的误差源，有必要特别关注一下三项指标：温漂，电压噪声，和负载调整。

2.2.3.2 量化误差

量化误差(Quantizing Error) 由于AD的有限分辩率而引起的误差，即有限分辩率AD的阶梯状转移特性曲线与无限分辩率AD（理想AD）的转移特性曲线（直线）之间的最大偏差。通常是1个或半个最小数字量的模拟变化量，表示为1LSB、1/2LSB。

2.2.3.3 失调误差与增益误差

失调误差与增益误差用数学公式可表达为：y=ax+b。其中，a为增益误差，b为失调误差。失调误差(Offset Error) 输入信号为零时输出信号不为零的值，可外接电位器调至最小。

2.2.3.4 线性度

线性度指标有两个：INL：翻译过来叫“积分非线性”，指的是ADC整体的非线性程度。DNL：翻译过来叫“微分非线性”，指的是ADC局部（细节）的非线性程度。
模数器件的精度指标是用积分非线性度（Interger NonLiner）即INL值来表示。也有的器件手册用 Linearity error 来表示。他表示了ADC器件在所有的数值点上对应的模拟值，和真实值之间误差最大的那一点的误差值。也就是，输出数值偏离线性最大的距离，单位是LSB（即最低位所表示的量）。比如12位ADC 的INL值为1LSB。那么，如果基准4.095V，测某电压得的转换结果是1000，那么，真实电压值可能分布在0.999~1.001V之间。
下面再说DNL值。理论上说，模数器件相邻量个数据之间，模拟量的差值都是一样的。就相一把疏密均匀的尺子。但实际并不如此。一把分辨率1毫米的尺子，相邻两刻度之间也不可能都是1毫米整。那么，ADC相邻两刻度之间最大的差异就叫差分非线性值（Differencial NonLiner）。DNL值如果大于1，那么这个ADC甚至不能保证是单调的，输入电压增大，在某个点数值反而会减小。这种现象在SAR（逐位比较）型ADC中很常见。举个例子，某12位ADC，INL=8LSB，DNL=3LSB（性能比较差），基准4.095V，测A电压读数1000，测B电压度数1200。那么，可判断B点电压比A点高197~203mV。而不是准确的200mV。
总结：（1）INL(Interger NonLinear,Linearity error)精度。理解为单值数据误差，对应该点模拟数据由于元器件及结构造成的不能精确测量产生的误差。（2）DNL(Differential NonLinear)差分非线性值。理解为刻度间的差值，即对每个模拟数据按点量化，由于量化产生的误差。

2.2.3.5 信噪比

图 信噪比

2.2.3.6 有效位数

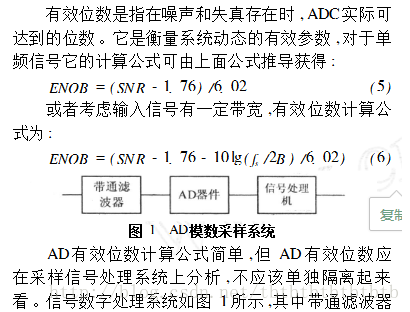
2.2.3.7 动态范围

3 参考文献

[1] 《A Glossary of Analog-to-Digital Specifications and Performance Characteristics》；
[2] 《理解AD转换器的性能参数》；
[3] 《Demystifying Sigma-Delta ADCs》；
[4] 《揭开Σ-ΔADC的神秘面纱》；

最后

以上就是清新季节为你收集整理的AD转换原理，器件与参数1 内容简介2 模数转换3 参考文献的全部内容，希望文章能够帮你解决AD转换原理，器件与参数1 内容简介2 模数转换3 参考文献所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。