【协同任务】基于matlab蚁群算法多无人机攻击调度【含Matlab源码 034期】

⛄一、多无人机协同作业简介

0 引言
多架无人机组成无人机集群可以协同完成任务，是未来无人机的发展方向。组成无人机集群的多架无人机通过机间链路互相通信实现协作，可以迅速准确地执行路径规划、协同侦察、协同感知和协同攻击等复杂任务。
为实现无人机集群协作的诱人前景，国内外都积极开展了相关研究工作。美国方面，美国国防预先研究计划局(DARPA)于2015年推出“小精灵”项目，计划研制具备自组织和智能协同能力的无人机蜂群系统。美国防部战略能力办公室(SCO)2014年启动了“无人机蜂群”项目，旨在通过有人机空射“灰山鹑”微型无人机蜂群执行低空态势感知和干扰任务。美国海军研究局(ONR)于2015年公布了“低成本无人机蜂群”(LOCUST)项目，研发可快速连续发射的无人机蜂群，无人机之间利用近距离射频网络共享态势信息，协同执行掩护、攻击或防御任务。2017年，在 DARPA 会议中心举办“进攻性集群战术”(OFFSET)项目的提案人活动，目标是发展基于游戏的开放架构，为城市作战的无人集群系统生成、评估和集成集群战术。
欧洲方面，2016 年，欧洲防务局启动了“欧洲蜂群”项目，开展了无人机蜂群的自主决策、协同飞行等关键技术研究。2016年，英国国防部发起无人机蜂群竞赛，参赛的多个团队控制无人机蜂群实现了通信中继、协同干扰、目标跟踪定位和区域测绘等任务。2017 年，俄罗斯无线电电子技术集团对外发表研究计划称，在战斗机上装载多架蜂群无人机可实现协同侦察和攻击的新型作战样式。
国内也相继展开相关研究。最近，中国电科(CETC)电子科学研究院发布了陆军协同无人机“蜂群”视频，引起广泛关注。
面对这一重要课题，本文研究总结了无人机协同应用的发展趋势，对其当前研究进展和发展方向进行了探讨，并提出无人机集群任务协作的发展趋势是多智能体协同。

1 无人机协同应用发展趋势
对现有研究工作的分析如图1所示，无人机协同应用大体上可以分为3个阶段，分别是分布式协同，群体智能协同和未来的多智能体协同。

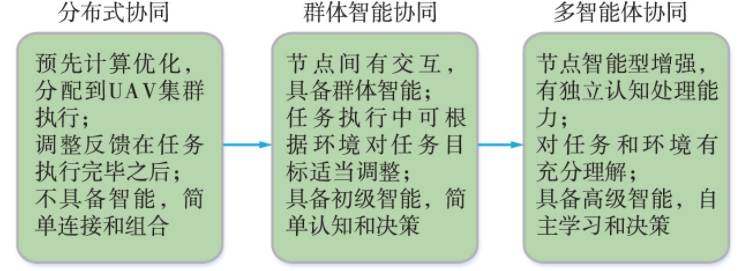
图1 无人机协同技术的发展趋势
无人机集群协同发展的第1个阶段是简单分布式协同。在该阶段，协同任务根据执行条件，预先在简单连接和组合的集群成员之间经过计算处理后分配执行。集群基本没有能力根据环境与目标的变化动态调整任务分配，各无人机分担的任务通常是确定的。

鉴于预分配方式的局限性，受生物集群活动的启发，群体智能被应用于无人机集群，使无人机集群协同发展到第2个阶段——群体智能协同。在该阶段中，各个无人机节点被赋予初级智能，能够进行简单的认知和决策；通过集群个体之间更为紧密的耦合，可以根据执行中的反馈调整优化方式或者优化目标，使整个无人机集群系统有能力构成自组织、高稳定的分布式系统。群体智能协同阶段当前正处于研究和应用迅速发展时期。

随着节点计算能力的进一步提升和人工智能技术的飞速发展，无人机协同即将进入发展的第3个阶段——多智能体协同。在多智能体协同发展阶段，集群中的各个无人机都将是一个独立的综合智能体，具有多维度认知计算和高级智能处理能力，从而实现更高效的自主学习和决策，并在此基础上，完成更复杂、更艰巨的任务。

2 分布式协同
从无人机集群出现开始就被用于解决协同路径规划、协同感知和协同任务规划等分布式协作任务。早期的无人机分布式协同任务通常都是提前进行充分的计算和分配，无人机节点按照既定算法或者方案予以执行。根据计算结果，分布式协同无人机群可组织执行配置好的任务，如图2所示。

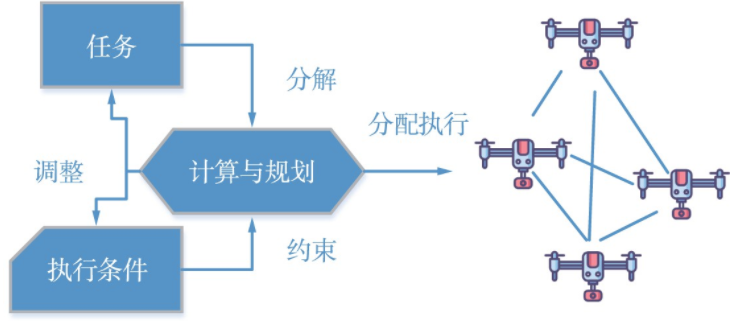
图2 分布式协同阶段的任务执行方式
2.1 协同路径规划
协同路径规划中，要求在给定目标或者搜索目标后，无人机节点根据当前的任务状态来确定飞行路径。针对协同搜索和跟踪任务的路线规划，无人机集群可采用最大化目标功能来检测最重要的目标，并在关键时刻对其进行跟踪，从而获得最有价值的信息。而协同搜索的路径规划可以分成无人机工作区间划分和全区域覆盖搜索路径规划2个子问题，将多机协同搜索转化为子区域上的单机搜索，对目标区域快速进行划分并生成飞行路线。基于改进遗传算法的多无人机协同侦察航迹规划算法，可用于解决面向复杂战场环境中高效侦察多种类型目标过程中的路径规划问题，并能够有效地提高航迹规划精度和效率。

2.2 协同感知
协同感知是多无人机集群共同探测感知某一目标区域状态的任务形式。在这类任务中最常见的是协同频谱感知。针对协同频谱感知任务特点，采用最佳融合准则的分布式协同任务执行方案可以优化检测性能，使协作频谱感知总错误率达到最小，并能降低协作感知时间，节省感知过程开销。

2.3 协同任务规划
协同任务规划要求集群系统能够根据目标任务和执行情况，对任务进行系统分配。例如，针对协同打击任务，通过建立无人机毁伤代价指标函数、航程代价指标函数和价值收益指标函数，可以实现多无人机协同打击任务的分配[5];而通过建立多目标优化模型并采用遗传算法，能有效提高任务的完成效率。针对协同搜救任务，使用一种新的基于通信保持的拍卖方法的自适应反馈调节遗传算法，能够改善传统遗传算法存在易陷入局部最优的弱点。

通过以上3种类型协同任务的相关研究工作可以看出，无人机集群的分布式协同方式虽然充分考虑了“分布式”特点，能够根据任务目标和集群特征，设置有效的目标函数和优化方法去寻求最优或者较优的结果，但是其任务执行环境和求解目标需要在任务执行之前进行优化计算，然后分配执行，不能适应实际中动态的任务目标和环境变化，缺乏“智能性”的感知和适应性行为。随着人们对“蜂群”“鸟群”等生物群体智能研究的深入，群体智能协同被进一步引入到无人机的协同中。

3 群体智能协同
“鸟群”“蚁群”等生物群体，虽然其中的个体智能有限，但是群体却展现出高度的自组织性，这一特点与无人机集群自主协同的需求相符，因而群体智能在无人机协同应用领域也得到了广泛研究，使无人机集群协同具有了初步的智能性。具备群体智能的无人机集群系统在任务拆解和执行过程中引入了群体反馈和适变能力，可执行较复杂的动态任务，其过程如图3所示。

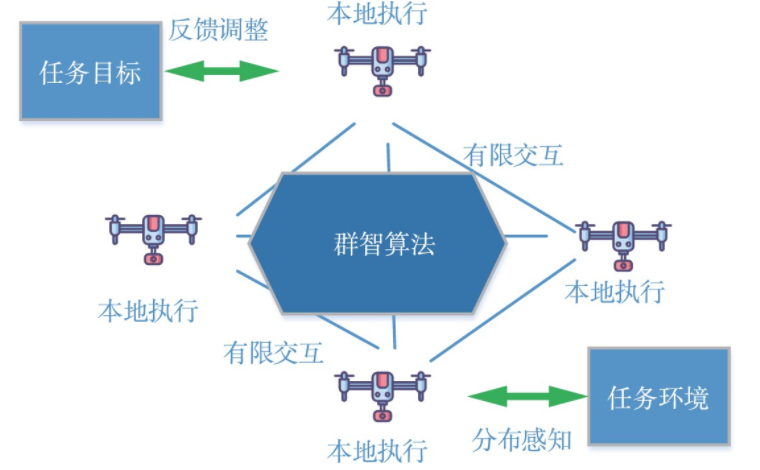
图3 群体智能协同阶段的任务执行方式
3.1 协同路径规划
山区路径规划任务受到地形特征的强烈影响，难以预先确定性分配执行，简单的分布式协同无法胜任。例如，为了执行山区应急物资运输的路径规划任务，一种考虑路径安全度的改进蚁群算法可快速收敛并生成更短路径。蚁群算法也被用于无人机协同飞抵空战场的航迹规划任务中;一种基于改进混沌蚁群算法更能克服传统蚁群智能算法中易出现局部极值、收敛效率低的缺陷，提升算法的全局寻优能力和搜索效率。针对协同攻击移动目标场景的航迹规划，另一种改进的蚁群算法建立了结合任务分配的无人机群协同航迹规划模型，可以快速地对地面多个移动目标规划出有效的航迹。

3.2 协同感知
在协同感知任务中，群体智能也得到应用。针对无人机集群通信场景和需求，出现了考虑结合认知无线电技术指导下的智能通信思想和汇聚有限智慧的群体智能理论方法，构建了群体智能协同通信模型和智能协同感知模型。

3.3 协同任务规划
协同作战是协同任务规划中的典型场景，结合群体智能优化算法的优势，基于粒子群-整数编码狼群算法的集群组网任务分配算法适合解决此类协同问题;由于无人机集群协同决策困难，还可以结合狼群算法的认知与协作能力，实现在复杂环境下迅速对目标进行跟踪和包围。这种协同任务，是第一类简单协同所不能胜任的。

虽然无人机集群和群体智能的结合可以充分发挥无人机集群优势，增强分布式协同智能性，可在任务执行过程中与环境和任务执行中间过程产生一定交互和反馈，使之具备一定的自适应能力，但是，这种智能仍然是非常有限的，其本质仍然是基于特定计算模式和反馈模式下的分布式优化算法。

4 多智能体协同
随着人工智能技术和节点自身算力的不断增强，未来无人机集群中的个体将具备更强的智能性，能够独立对环境和任务进行感知和评估，实现多个智能体之间的交互和协同，从而具备多智能体协同能力。

近年来，人工智能领域研究取得了突破性进展。其中，深度强化学习在诸多领域得到了成功应用。无线通信网络基于多智能体深度强化学习的资源分配技术也得到了深入研究。多智能体深度强化学习模型早已被用于解决车联网中频谱资源分配问题,这种应用已经与无人机集群系统颇为接近。例如一种基于多智能体深度强化学习的分布式动态功率分配方案。基于多智能体深度强化学习的策略还可被用于二者的结合——用无人机辅助车辆网络进行多维资源管理。

虽然基于强化学习的多智能体通信网络资源分配问题已经得到了广泛研究，但是由于网络特性的不同，传统的针对其他通信网络的研究成果不能直接用于无人机集群网络。因而基于强化学习的多智能体自主协同应用逐渐成为未来无人机多智能体自主协同的一个研究热点。针对无人机群的通信网络资源动态分配问题而提出的多智能体深度强化学习方案也陆续出现,例如，一种基于多智能体深度强化学习的分布式干扰协调策略被用于受到干扰的无人机网络中的文件下载业务。智能体在适用于无人机网络特点的独立强化学习中，其行为策略通常只能根据它们对全局环境的局部个体观察来制定。针对这种局限性，联合采用2种不同规模的智能体可解决智能体之间的通信问题。

无人机集群协同，经常会处理动态高维离散和连续动作状态空间的优化求解问题，近来出现的演员-评论家算法是深度强化学习的一个新兴方向，结合了基于值函数和基于策略函数的深度强化学习两大分支的优势，非常适用于无人机集群的智能协同。利用演员-评论家算法，在无线信道和可再生能源再生率都是随机变化，且环境动态变化条件下，可寻求资源分配最佳策略,如用于解决车联网中复杂动态环境下的资源分配问题。应用设备到设备(D2D)网络的异构蜂窝网络环境下，基于演员-评论家算法的策略可用于智能化节能模式选择和资源分配。

随着节点智能算力的不断增强，无人机集群中的每架无人机可以作为一个具有深度强化学习能力的智能体，而整个集群可通过合作构成多智能体。相邻无人机之间通过通信网络进行信息交换与分发。如图4所示，每架无人机都与局部环境相互作用，根据从周围环境或者同伴无人机得到的信息，针对承载的任务需求，通过深度强化学习，智能地产生动作策略，进行自身资源与行为的分配与调整，进而与环境和同伴互动，并获得个体奖励。

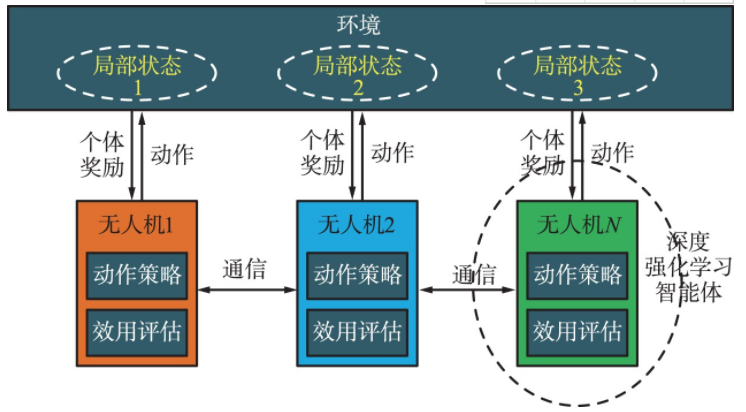
图4 基于多智能体的无人机集群
每架无人机的深度强化学习智能体由2个深度神经网络构成，包括演员网络和评论家网络，如图5所示。

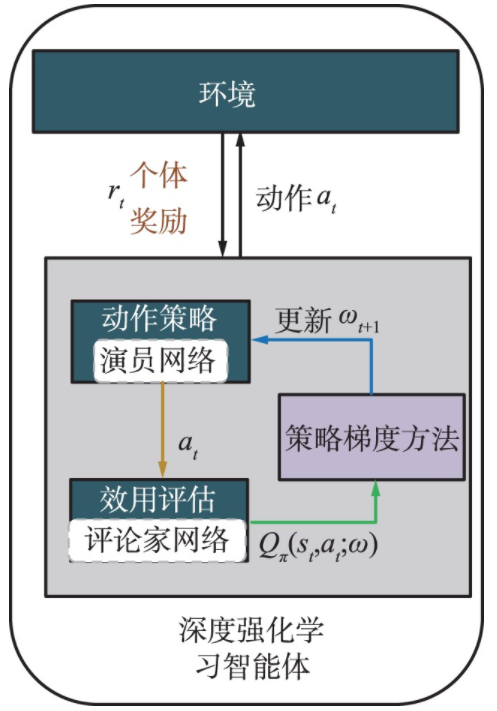
图5 基于演员评论家算法的无人机智能体
演员网络负责输出动作，评论家网络负责评价演员的动作，以获得相互促进的效果。与传统的深度强化学习方法相比，演员-评论家算法同时吸取了基于值函数方法和基于策略函数方法的优点，从价值和策略两方面来训练提升智能体，训练的更快，效果也更好。通过训练和学习，期望智能体的评论家网络可以获得最佳效用评估函数：

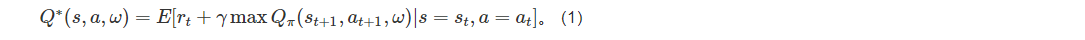
智能体从周围环境中观察得到状态信息St ,例如干扰状态、相邻无人机等。演员网络拟合动作策略函数π(St;ωπ),根据状态信息St,动作策略函数输出当前时隙的动作at,也就是资源分配结果，并应用到环境中得到个体的即时奖励rt。奖励由奖励函数计算得到，负责反馈一个即时的、合理的、具有指导意义的奖励值，从而激励智能体向目标更新策略。评论家网络拟合效用评估函数Q(St,at,ω),负责预测和评估在当前状态St采用动作at所能得到的状态动作价值，即长期性回报Rt为：

式中，γ是折扣因子，γ表示了当前对于未来收益的重视程度，取值在0～1之间，取值0则表示智能体忽视未来收益，只看重当前的收益rt,取值1则表示智能体将未来每个时刻的收益都视为与当前时刻收益一样的重要性。获得最大的长期性回报是智能体的最终目的，这个目标可以根据任务的性质被定义为不同的评判标准。

评论家网络的最佳效用评估函数对应的演员网络动作策略即为最佳动作策略π*。动作策略函数的参数通过策略梯度的方法进行更新，效用评估函数的参数采用最小化损失函数进行更新：

式中，yt为优势函数，用来衡量计算执行动作后的实际效用评估值。通过更新，智能体的演员网络的动作策略输出的动作越来越好，而评论家网络的效用评估也会越来越准确。基于多智能体的无人机群的每架无人机都会朝着收益最大的方向执行动作，从而实现集群的收益最大化。

⛄二、蚁群算法简介

1 蚁群算法(ant colony algorithm,ACA)起源和发展历程
Marco Dorigo等人在研究新型算法的过程中，发现蚁群在寻找食物时，通过分泌一种称为信息素的生物激素交流觅食信息从而能快速的找到目标，于是在1991年在其博士论文中首次系统地提出一种基于蚂蚁种群的新型智能优化算法“蚂蚁系统（Ant system,简称AS）”，后来，提出者及许多研究者对该算法作了各种改进，将其应用于更为广泛的领域，如图着色问题、二次分配问题、工件排序问题、车辆路径问题、车间作业调度问题、网络路由问题、大规模集成电路设计等。近些年来，M.Dorigo等人把蚂蚁算法进一步发展成一种通用的优化技术“蚁群优化（Ant Colony Optimization,简称ACO）”，并将所有符合ACO框架的算法称为“蚁群优化算法（ACO algorithm）”。

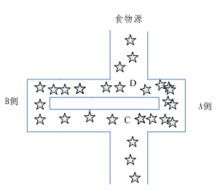
具体来说，各个蚂蚁在没有事先告知食物在什么地方的前提下开始寻找食物。当一只找到食物以后，它会向环境释放一种挥发性分泌物pheromone (称为信息素,该物质随着时间的推移会逐渐挥发消失，信息素浓度的大小表征路径的远近)信息素能够让其他蚂蚁感知从而起到一个引导的作用。通常多个路径上均有信息素时，蚂蚁会优先选择信息素浓度高的路径，从而使浓度高的路径信息素浓度更高，形成一个正反馈。有些蚂蚁并没有像其它蚂蚁一样总重复同样的路，他们会另辟蹊径，如果另开辟的道路比原来的其他道路更短，那么，渐渐地，更多的蚂蚁被吸引到这条较短的路上来。最后，经过一段时间运行，可能会出现一条最短的路径被大多数蚂蚁重复着。最终，信息素浓度最高的路径即是最终被蚂蚁选中的最优路径。
与其他算法相比，蚁群算法是一种比较年轻的算法，具有分布式计算、无中心控制、个体之间异步间接通信等特点，并且易于与其他优化算法相结合，经过不少仁人志士的不断探索，到今天已经发展出了各式各样的改进蚁群算法，不过蚁群算法的原理仍是主干。

2 蚁群算法的求解原理
基于上述对蚁群觅食行为的描述，该算法主要对觅食行为进行以下几个方面模拟：
（1）模拟的图场景中包含了两种信息素，一种表示家，一种表示食物的地点，并且这两种信息素都在以一定的速率进行挥发。
（2）每个蚂蚁只能感知它周围的小部分地方的信息。蚂蚁在寻找食物的时候，如果在感知范围内，就可以直接过去，如果不在感知范围内，就要朝着信息素多的地方走，蚂蚁可以有一个小概率不往信息素多的地方走，而另辟蹊径，这个小概率事件很重要，代表了一种找路的创新，对于找到更优的解很重要。
（3）蚂蚁回窝的规则与找食物的规则相同。
（4）蚂蚁在移动时候首先会根据信息素的指引，如果没有信息素的指引，会按照自己的移动方向惯性走下去，但也有一定的机率改变方向，蚂蚁还可以记住已经走过的路，避免重复走一个地方。
（5）蚂蚁在找到食物时留下的信息素最多，然后距离食物越远的地方留下的信息素越少。找到窝的信息素留下的量的规则跟食物相同。蚁群算法有以下几个特点:正反馈算法、并发性算法、较强的鲁棒性、概率型全局搜索、不依赖严格的数学性质、搜索时间长，易出现停止现象。
蚂蚁转移概率公式：

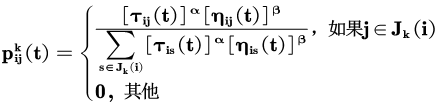
公式中：是蚂蚁k从城市i转移到j的概率；α，β分别为信息素和启发式因子的相对重要程度；为边（i，j）上的信息素量；为启发式因子；为蚂蚁k下步允许选择的城市。上述公式即为蚂蚁系统中的信息素更新公式，是边（i,j)上的信息素量；ρ是信息素蒸发系数，0<ρ<1;为第k只蚂蚁在本次迭代中留在边（i,j）上的信息素量；Q为一正常系数；为第k只蚂蚁在本次周游中的路径长度。
在蚂蚁系统中，信息素更新公式为：

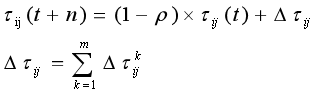
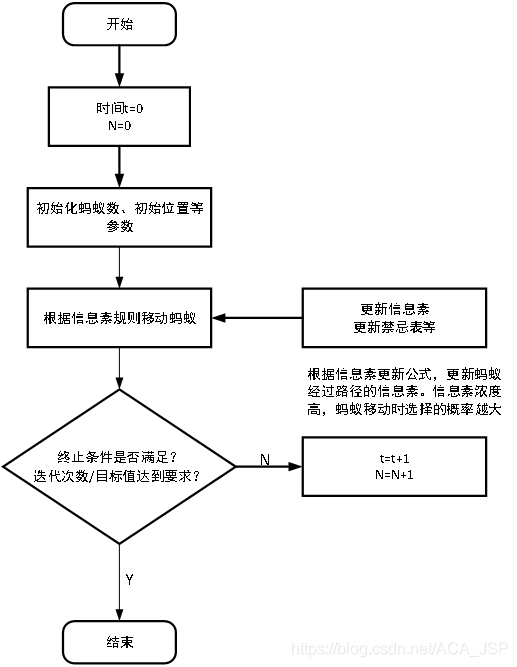
3 蚁群算法的求解步骤：
（1）初始化参数在计算之初，需要对相关参数进行初始化，如蚁群规模（蚂蚁数量）m、信息素重要程度因子α、启发函数重要程度因子β、信息素会发银子ρ、信息素释放总量Q、最大迭代次数iter_max、迭代次数初值iter=1。
（2）构建解空间将各个蚂蚁随机地置于不同的出发点，对每个蚂蚁k（k=1,2,3…m），按照（2-1）计算其下一个待访问城市，直到所有蚂蚁访问完所有城市。
（3）更新信息苏计算每个蚂蚁经过路径长度Lk(k=1,2,…，m），记录当前迭代次数中的最优解（最短路径）。同时，根据式（2-2）和（2-3）对各个城市连接路径上信息素浓度进行更新。
（4） 判断是否终止若iter<iter_max，则令iter=iter+1,清空蚂蚁经过路径的记录表，并返回步骤2；否则，终止计算，输出最优解。
（5）判断是否终止若iter<iter_max，则令iter=iter+1,清空蚂蚁经过路径的记录表，并返回步骤2；否则，终止计算，输出最优解。3. 判断是否终止若iter<iter_max，则令iter=iter+1,清空蚂蚁经过路径的记录表，并返回步骤2；否则，终止计算，输出最优解。

⛄三、部分源代码

t=[4 5;16 25.8;10 45;20 55;30 65;35 55;29 31;37 26;47 27;30 31.3;31 17;14 7;35.6 13.8;26.7 22.5;21 39;38 42;5 26;28 53;20 13;10 60;26 31;54 38;7 58;12 36;30 2] %24个点,第25个点事origin
save t.mat t
load t.mat
value=[1 1 1 2 3 2 1 3 3 2 2 2 2 2 1 2 3 3 1 1 2 1 1 1]; %24个目标的价值
value=value/100;
time=zeros(1,25); %侦察UAV时间数组，里面放的是飞机走的航程，除以速度便是时间，设速度为‘1’
attacktime=zeros(1,25); %打击UAV时间数组
%把侦察过的任务对应无人机走过的航程存到该任务的一个矩阵里，当做时间，然后打击任务如果选定某任务，check一下时间是否合格，合格的话，可以打击，并存入禁忌表，不合格的话，选次概率的

%注：目的是把所有目标执行完所有任务，所以每次迭代最后所有无人机收获的总价值都一样，都是所有目标的价值之和；所以本程序考虑优先执行价值大的目标，防止无人机飞很久、打很久后攻打效率变低
%的情况出现

%%计算城市间相互距离
n=size(t,1);
D=zeros(n,n);
for i=1:n
for j=1:n
if i~=j
D(i,j)=sqrt(sum((t(i,:)-t(j,:)).^2));
else
D(i,j)=1e-2;
end
end
end
%%初始化参数
m=10; %蚂蚁个数
alpha=1; %信息素重要程度因子
beta=1; %启发函数重要程度因子
gama=2;
rho=0.3; %信息素挥发因子
Q=1.0; %总量
eta=1./D; %启发函数
tau=ones(n,n)+7.1192e-005;%信息素矩阵
iter=1; %迭代次数初始值
iter_max=80; %迭代次数最大值
length_best=zeros(iter_max,1);%每次迭代最佳路径长度(应该是一次比一次小)
length_ave=zeros(iter_max,1); %每次迭代路径平均长度
%%迭代寻找最佳路径
while iter<=iter_max
whta=cell(8,1);
lieend=zeros(8,1);
for zu=1:8
city_index=1:25; %城市来标号
table=[];
start=zeros(4,1);
temp=randperm(24);
for i=1:4
start(i)=temp(i);
end
table(:,1)=start;
j=2;
while (j<=30)
for i=1:4
if i1 %UAV1只负责“侦察”任务
if table(1,(j-1))~=25
table1=table(1,:);
table1=[table1;table(3:4,:)];
tabu1=table1(????; %UAV1的禁忌表出来了 %25如果也在tabu1里的话，那么
allow_index1=~ismember(city_index,tabu1); %【走过的变成0，能走的为1】【若tabu=(1 4)则allow_index=(0 1 1 0 1 1 1…)】【注意：allow_index与city_index同维】
allow1=city_index(allow_index1); %把还能走的序号摘出来了（待访问的城市集合）
P1=allow1;
%计算城市的转移概率
if numel(allow1)~=0
for k=1:max(size(allow1))-1
P1(k)=(tau(table(1,(j-1)),allow1(k))^{alpha)*(eta(table(1,(j-1)),allow1(k))}beta)10000+7.1192e-004;
end
P1(max(size(allow1)))=7.1192e-005;
P1=P1/sum(P1);
[d1,ind1]=sort(P1,2,‘descend’);%从大到小排序是d1,对应的原序号是ind1
target1=allow1(ind1(1));
%轮盘赌法选择下一个城市
%pc1=cumsum(P1); % （p1 p1+p2 p1+p2+p3 p1+p2+p3+p4 …）【p1<->allow(1) p2<->allow(2) …】
%target_index1=find(pc1>=rand);
%target1=allow1(target_index1(1)); %这次返回的是allow数组中城市的真正序号
table(1,j)=target1; %把选好这个点放到路径表里面
rr=D(25,table(1,1));
time(table(1,1))=rr;
if j>2
for c=2:(j-1)
rr=rr+D(table(1,c-1),table(1,c));
end
end
rrr=rr+D(table(1,j-1),target1);%rrr就是UAV1到该点时走过的航程
time(target1)=rrr;
else
table(1,j)=25;
end
end
if table(1,(j-1))25
table(1,j)=25;
end
end
if i2 %UAV2只负责“打击”任务
if (table(2,(j-1))~=25)
table(2,1)=table(1,1); %设定它第一次打击的是UAV1侦察过的目标
ta2=table(1:(4(j-1)+1)); %当前元素之前所有的元素
tabu21=[];
tabu22=[];
tabu2=[];
for y=1:24
if sum(ta2y)2
tabu21=[tabu21;y];
end
end %出现过两次的放在tabu21里
tabu22=setdiff(1:24,ta2); %一次都没出现的放在tabu22里
tabu2=[tabu21’,tabu22]; %tabu2出来了
allow_index2=~ismember(city_index,tabu2); %【走过的变成0，能走的为1】【若tabu=(1 4)则allow_index=(0 1 1 0 1 1 1…)】【注意：allow_index与city_index同维】
allow2=city_index(allow_index2); %把还能走的序号摘出来了（待访问的城市集合）
P2=allow2;
%计算城市的转移概率
for k=1:(length(allow2)-1)
P2(k)=tau(table(2,(j-1)),allow2(k))*eta(table(2,(j-1)),allow2(k))*value(allow2(k))10000;
end
P2(max(size(allow2)))=7.1192e-005;
P2=P2/sum(P2);
[d2,ind2]=sort(P2,2,‘descend’);%从大到小排序是d1,对应的原序号是ind1
target2=allow2(ind2(1)); %target2=d1(1);
%轮盘赌法选择下一个城市
%pc2=cumsum(P2); % （p1 p1+p2 p1+p2+p3 p1+p2+p3+p4 …）【p1<->allow(1) p2<->allow(2) …】
%target_index2=find(pc2>=rand); %选中那个概率较大的选中的点，返回的是allow数组中的序号
%target2=allow2(target_index2(1)); %这次返回的是allow数组中城市的真正序号
%table(2,j)=target2; %把选好这个点放到路径表里面
oo=D(25,table(2,1));
attacktime(table(2,1))=oo;
if j>2
for c=2:(j-1)
oo=oo+D(table(2,c-1),table(2,c));
end
end
ooo=oo+D(table(2,j-1),target2);%ooo就是UAV2到该点时走过的航程
if numel(d2)>5
u=2;
while (ooo>time(target2)+20 & u<6)
target2=allow2(ind2(u));
ooo=oo+D(table(2,(j-1)),target2);
u=u+1;
end
end
table(2,j)=target2;
attacktime(target2)=ooo;
end
if table(2,(j-1))25
table(2,j)=25;
end
end
if i3 %UAV3是“察打”任务
if table(3,(j-1))~=25
ta3=table(1:(4(j-1)+2));
tabu3=[];
tabu3c=[];
for y=1:24
if sum(ta3y)2
tabu3=[tabu3;y];
end
end %出现两次的放在tabu3里
for y=1:24
if sum(ta3y)==1
tabu3c=[tabu3c;y];
end
end %tabu3c是待打的任务，已侦查完的任务
allow_index3=~ismember(city_index,tabu3); %【走过的变成0，能走的为1】【若tabu=(1 4)则allow_index=(0 1 1 0 1 1 1…)】【注意：allow_index与city_index同维】
allow3=city_index(allow_index3); %把还能走的序号摘出来了（待访问的城市集合）
P3=allow3;
%计算城市的转移概率
for k=1:(length(allow3)-1)
%if ismember(allow3(k),tabu3c)1
h=table(3,(j-1))
P3(k)=(tau(table(3,j-1),allow3(k))^{alpha)*(eta(table(3,(j-1)),allow3(k))}beta)*value(allow3(k))*10000+7.1192e-005;%这是要打的，需要价值
%else
%P3(k)=(tau(table(3,(j-1)),allow3(k))^{alpha)*(eta(table(3,(j-1)),allow3(k))}beta)100+7.1192e-005;%这些是待侦察的，没有价值
%end
end
P3(max(size(allow3)))=7.1192e-009;
P3=P3/sum(P3);
[d3,ind3]=sort(P3,2,‘descend’);%从大到小排序是d1,对应的原序号是ind1
target3=allow3(ind3(1));
%轮盘赌法选择下一个城市
%pc3=cumsum(P3); % （p1 p1+p2 p1+p2+p3 p1+p2+p3+p4 …）【p1<->allow(1) p2<->allow(2) …】
%target_index3=find(pc3>=rand); %选中那个概率较大的选中的点，返回的是allow数组中的序号
%target3=allow3(target_index3(1)); %这次返回的是allow数组中城市的真正序号
%table(3,j)=target3; %把选好这个点放到路径表里面
ww=D(25,table(3,1));
time(table(3,1))=ww;
if j>2
for c=2:(j-1)
ww=ww+D(table(3,c-1),table(3,c));
end
end
www=ww+D(table(3,j-1),target3);%www就是UAV3到该点时走过的航程
if ismember(target3,tabu3c)==0 %侦察任务
time(target3)=www;
table(3,j)=target3;
else %打击任务
attacktime(target3)=www;
if numel(d3)>5
u=2;
while (www>time(target3)+20 & u<6)
target3=allow3(ind3(u));
www=ww+D(table(3,(j-1)),target3);
u=u+1;
end
end
attacktime(target3)=www;
table(3,j)=target3;%www<time(target3)+10 说明此打击任务合理
end
end
if table(3,(j-1))25
table(3,j)=25;
end
end
if i4 %UAV4是“察打”任务
if table(4,(j-1))~=25
ta4=table(1:(4(j-1)+3));
tabu4=[];
tabu4c=[];
for y=1:24
if sum(ta4y)2
tabu4=[tabu4;y];
end
end %出现两次的放在tabu4里、、可以把已经侦察过的放在tabu4c中，（即出现过一次的），如果选到的是在tabu4’中的说明是要打击的然后算一下它的航程，再和侦察路径比较
for y=1:24
if sum(ta4y)==1
tabu4c=[tabu4c;y];
end
end
allow_index4=~ismember(city_index,tabu4); %【走过的变成0，能走的为1】【若tabu=(1 4)则allow_index=(0 1 1 0 1 1 1…)】【注意：allow_index与city_index同维】
allow4=city_index(allow_index4); %把还能走的序号摘出来了（待访问的城市集合）
P4=allow4;
%计算城市的转移概率
for k=1:(max(size(allow4))-1)
%if ismember(allow4(k),tabu4c)==1
sxx=table(4,(j-1))
P4(k)=(tau(table(4,(j-1)),allow4(k))^{alpha)*(eta(table(4,(j-1)),allow4(k))}beta)*value(allow4(k))*10000+7.1192e-005;
%else
%P4(k)=(tau(table(4,(j-1)),allow4(k))^{alpha)*(eta(table(4,(j-1)),allow4(k))}beta)*100+7.1192e-005;
%end
end
P4(max(size(allow4)))=7.1192e-009;
P4=P4/sum(P4);
[d4,ind4]=sort(P4,2,‘descend’);%从大到小排序是d1,对应的原序号是ind1
target4=allow4(ind4(1));
%轮盘赌法选择下一个城市
%pc4=cumsum(P4); % （p1 p1+p2 p1+p2+p3 p1+p2+p3+p4 …）【p1<->allow(1) p2<->allow(2) …】
%target_index4=find(pc4>=rand); %选中那个概率较大的选中的点，返回的是allow数组中的序号
%target4=allow4(target_index4(1)); %这次返回的是allow数组中城市的真正序号
%table(4,j)=target4; %把选好这个点放到路径表里面
qq=D(25,table(4,1));
time(table(4,1))=qq;
if j>2
for c=2:(j-1)
qq=qq+D(table(4,c-1),table(4,c));
end
end
qqq=qq+D(table(4,j-1),target4);%www就是UAV3到该点时走过的航程
if ismember(target4,tabu4c)==0 %侦察任务
time(target4)=qqq;
table(4,j)=target4;
else %打击任务
attacktime(target4)=qqq;
if numel(d4)>5
u=2;
while (qqq>time(target4)+20 & u<6)
target4=allow4(ind4(u));
qqq=qq+D(table(4,j-1),target4);
u=u+1;
end
end
attacktime(target4)=qqq;
table(4,j)=target4;%www<time(target4)+10 说明此打击任务合理
end
end
if table(4,(j-1))==25
table(4,j)=25;
end
end
end %一列结束

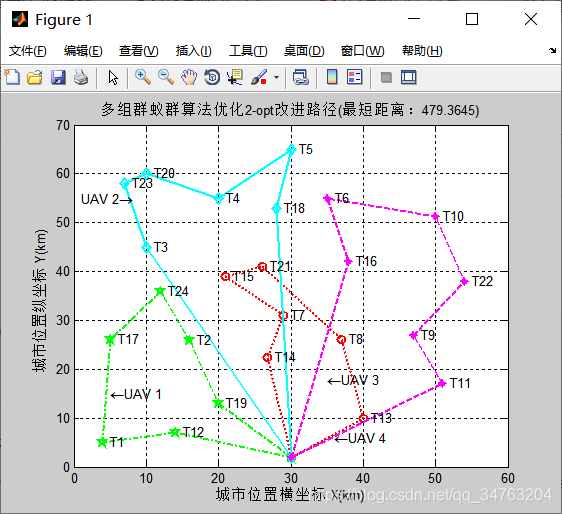
⛄四、运行结果

⛄五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]揭东,汤新民,陈济达,李腾.改进蚁群算法的多无人机冲突解脱技术研究[J].武汉理工大学学报(交通科学与工程版). 2020,44(01)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除

最后

以上就是俊秀巨人为你收集整理的【协同任务】基于matlab蚁群算法多无人机攻击调度【含Matlab源码 034期】的全部内容，希望文章能够帮你解决【协同任务】基于matlab蚁群算法多无人机攻击调度【含Matlab源码 034期】所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。