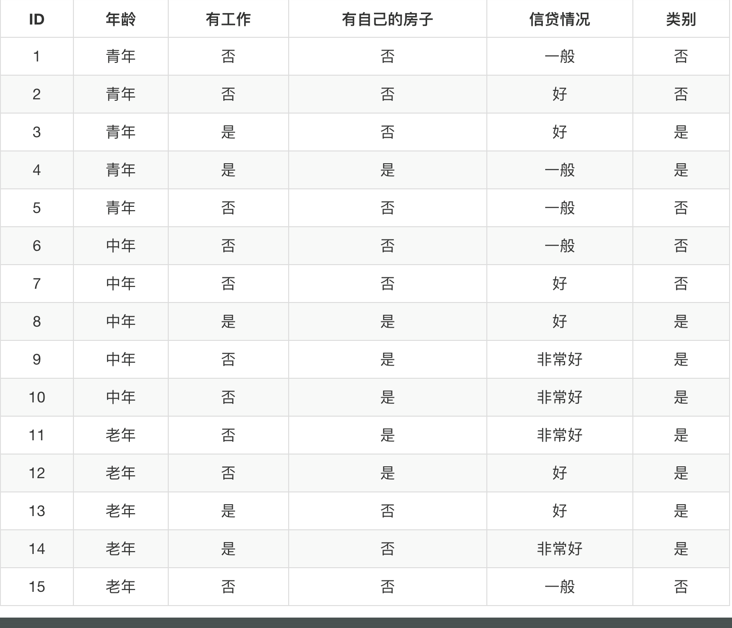
什么是决策树
先看一个例子
你母亲要给你介绍男朋友,是这么来对话的:
女儿:多大年纪了
母亲:26
女儿:长的帅不帅?
母亲:挺帅的。
女儿:收入高不?
母亲:不算很高,中等情况。
女儿:是公务员不?
母亲:是,在税务局上班呢。
女儿:那好,我去见见。
以上一段对话可以用下图来表示
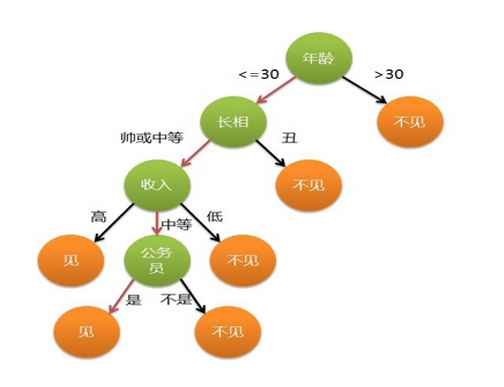
决策树就是一种基于树的结构,它模仿了人类在做决策时的判断。
决策树的划分依据
再看一个例子,一个人要去银行贷款,银行的柜员需要对他的各种信息进行查验,最后绝对是否对其提供贷款服务,某些贷款数据如下
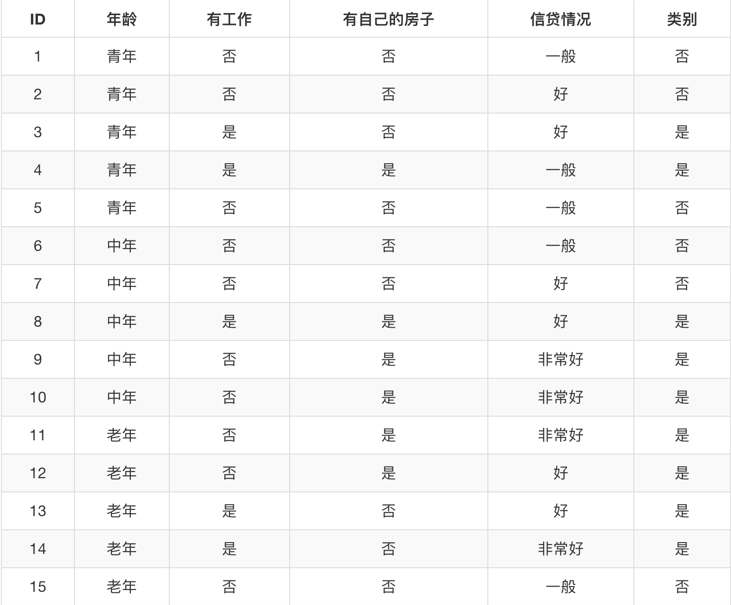
当我们对该客户进行判断的时候,这些信息是有重要性的,越关键的信息就要放在前面,这样可以减少更多的不确定性,尽快淘汰不符合条件的用户,实际划分情况如下
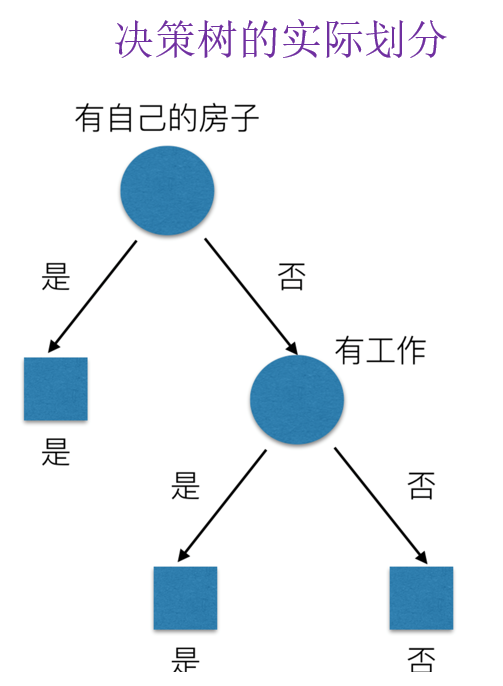
上图认为,是否有房是最重要的特征, 那么我们如何考量每一个特征他的重要性呢?
再来看一个例子,假设有32支球队,当我们不知道任何一支球队的信息时,每猜一次需要付出点儿代价:一块钱, 如何利用最短的次数猜中冠军?
那就要用到我们小学二年级就学过的二分法了,我们可以把球编上号,从1到32,然后提问:冠军在1-16号吗?依次询问,只需要五次,就可以知道结果。
32支球队我们需要猜log₂32 = 5次, 64支球队我们需要log₂64 = 6次。
当我们不知道任何一支球队的信息时,即每只球队获胜的概率都是1/32,我们猜到冠军的’代价’就要大一些,它的’代价’为:
5
=
−
[
1
32
l
o
g
2
1
32
+
1
32
+
.
.
.
]
5=-[frac{1}{32}log_2frac{1}{32}+frac{1}{32}+...]
5=−[321log2321+321+...](共有32项)
当我们开放一些数据信息,“谁是世界杯冠军”的信息量应该比5比特少, 例如我们已知,中国队获得世界杯冠军的概率为½,巴西队1/6,德国队为¼
那么猜对冠军的代价为
−
[
1
2
l
o
g
2
1
2
+
[
1
4
l
o
g
2
1
4
+
[
1
6
l
o
g
2
1
6
+
.
.
.
]
<
5
-[frac{1}{2}log_2frac{1}{2}+[frac{1}{4}log_2frac{1}{4}+[frac{1}{6}log_2frac{1}{6}+...]<5
−[21log221+[41log241+[61log261+...]<5
我们称这种’代价’为信息熵
在信息论当中,信息的单位:比特
一个离散型随机变量X的熵H(X)定义为:
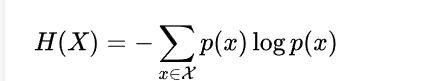
决策树的分类依据之一:信息增益
信息增益表示得知特征X的信息而使得类Y的信息的不确定性减少的程度,信息增益越大,意味着包含的信息量越大
特征A对训练数据集D的信息增益g(D,A),定义为:
集合D的信息熵H(D)与特征A给定条件下D的信息条件熵H(DIA)之差,即公式为:
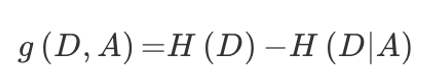
还是刚才这个例子
信息熵
H
(
D
)
=
−
(
9
15
l
o
g
9
15
+
6
15
l
o
g
6
15
)
=
0.971
H(D)=-(frac{9}{15}logfrac{9}{15}+frac{6}{15}logfrac{6}{15})=0.971
H(D)=−(159log159+156log156)=0.971
注:信息熵是根据目标值求的,这里目标值’是’为9种,‘否’为6种
这里我们选取特征’年龄’
g(D,年龄) = H(D) - H(D’|年龄)
条件熵的计算:
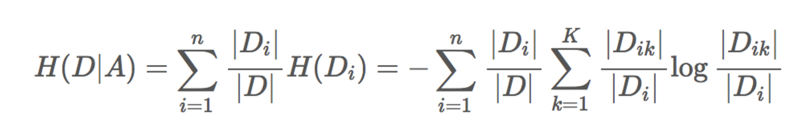
H(D’|年龄) = [
1
3
frac{1}{3}
31H(青年) +
1
3
frac{1}{3}
31H(中年) +
1
3
frac{1}{3}
31H(老年)]
H (青年) =
−
(
2
5
l
o
g
2
5
+
3
5
l
o
g
3
5
)
-(frac{2}{5}logfrac{2}{5}+ frac{3}{5}logfrac{3}{5})
−(52log52+53log53)
H(中年)=
(
2
5
l
o
g
2
5
+
3
5
l
o
g
3
5
)
(frac{2}{5}logfrac{2}{5}+ frac{3}{5}logfrac{3}{5})
(52log52+53log53)
H(老年)=
−
(
4
5
l
o
g
4
5
+
4
5
l
o
g
4
5
)
-(frac{4}{5}logfrac{4}{5}+ frac{4}{5}logfrac{4}{5})
−(54log54+54log54)
得到g(D,年龄)
同理我们也可以得到 g(D,有工作)、g(D,有自己的房子)、g(D,信贷情况)
最后通过比较,得到有自己的房子这个特征的信息增益最大。
代码实现如下:
"""
sklearn决策树API
class sklearn.tree.DecisionTreeClassifier(criterion='gini,max_depth=None,random state=None)
决策树分类器
criterion:默认是gini系数,也可以选择信息增益的熵'entropy'
max_depth:树的深度大小
random_state:随机数种子
method:decision_path:返回决策树的路径
"""
"""
在泰坦尼克号和titanic2数据帧描述泰坦尼克号上的个别乘客的生存状态。
在泰坦尼克号的数据帧不包含从剧组信息,但它确实包含了乘客的一半的实际年龄。
关于泰坦尼克号旅客的数据的主要来源是百科全书Titanica。
这里使用的数据集是由各种研究人员开始的。其中包括许多研究人员创建的旅客名单,由Michael A. Findlay编辑。
我们提取的数据集中的特征是票的类别,存活,乘坐班,年龄,登陆,
home.dest,房间,票,船和性别。乘坐班是指乘客班(1,2,3),是社会经济阶层的代表。
其中age数据存在缺失。
"""
"""
sklearn.tree.export_graphviz()该函数能够导出DOT格式
tree.export_graphviz(estimator,out_file='tree.dot',feature_names=['',''])
"""
import pandas as pd
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, export_graphviz
def decision():
"""
决策树对泰坦尼克号乘客预测生死
:return:
"""
# 获取数据
titanic = pd.read_csv('./titanic.txt')
# 处理数据,选取三个特征和目标值
x = titanic[['pclass', 'age', 'sex']]
y = titanic[['survived']]
# 处理缺失值
x['age'].fillna(x['age'].mean(), inplace=True)
# 分割数据集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25)
print(x_train)
# 进行处理(one-hot编码)
dict1 = DictVectorizer(sparse=False)
# orient='records'参数表示把一行转换成字典
x_train_dict = x_train.to_dict(orient='records')
x_test_dict = x_test.to_dict(orient='records')
x_train = dict1.fit_transform(x_train_dict)
x_test = dict1.fit_transform(x_test_dict)
print('x_train:n', x_train)
print(dict1.get_feature_names_out())
# 用决策树进行预测
dec = DecisionTreeClassifier()
dec.fit(x_train, y_train)
# 预测准确率
print('预测的准确率:', dec.score(x_test, y_test))
# 导出决策树的结构
export_graphviz(dec, out_file='./titanic.dot',
feature_names=['age', 'pclass=1st', 'pclass=2nd', 'pclass=3rd',
'sex=female', 'sex=male'])
if __name__ == '__main__':
decision()
决策树的分类还有其他依据
ID3
信息增益最大的准则
•C4.5
信息增益比最大的准则
CART
回归树:平方误差最小
分类树:基尼系数最小的准则在sklearn中可以选择划分的原则
优点:
··简单的理解和解释,树木可视化。
··需要很少的数据准备,其他技术通常需要数据归一化
缺点:
··决策树学习者可以创建不能很好地推广数据的过于复杂的树,这被称为过拟合。
··决策树可能不稳定,因为数据的小变化可能会导致完全不同的树被生成
改进:
减枝cart算法(决策树API已经实现)
随机森林
减枝cart算法:
在DecisionTreeClassifier类中,有两个参数
min_samples_split=2, min_samples_leaf=1
来确定结点的分支,和结点样本最低数量
最后
以上就是老迟到康乃馨最近收集整理的关于机器学习07:决策树基本流程什么是决策树决策树的划分依据决策树的分类依据之一:信息增益的全部内容,更多相关机器学习07:决策树基本流程什么是决策树决策树内容请搜索靠谱客的其他文章。








发表评论 取消回复