堆排序算法

1. 构建最小堆
2. 取出最小堆第一个元素（最小值）
3. 剩下的数据构造最小堆（反复执行2,3直到取出所有的值为止）

数组[72,23,5,68,94,16,71,84,76]表示的树构造最小堆：

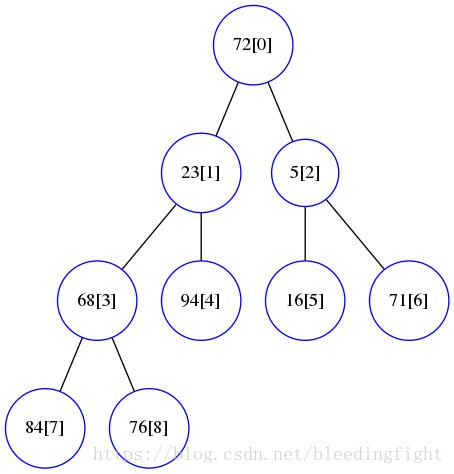
最小堆的元素有如下关系：
- 节点k的左右节点为2*k+1,2*k+2 ,你如节点5（index=2）左边节点71(index=2*2+1),右边节点84(index=2*2+1)

尽管这个图满足乐这个关系，但是不满足另一个关系（这个图不是最小堆）：
- 节点的字节点都比节点大。
构造生成的最小堆：

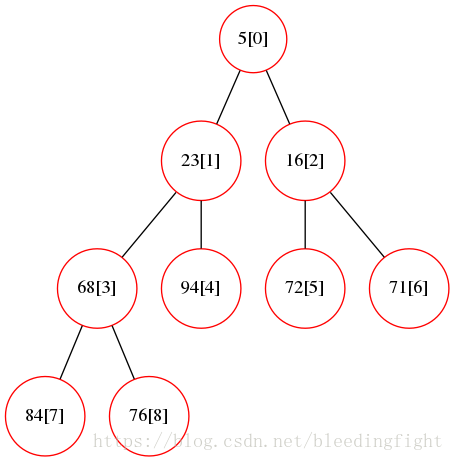
如何通过节点k获取父节点信息？
k/2 就是父节点索引（如果除不尽则舍去小数点，代码中因为是整数除，所以不用管。）
非叶子节点的个数length(array)/2-1
构造最小堆，从根节点开始，如果根节点的左子节点小于根节点，就找根节点孩子节点中更小的值，找到后将值和根节点的值交换，然后沿着下一个节点继续查找（查找不需要找叶子节点，因为叶子节点没有孩子，所以只需要查找length(array)/2-1）个节点。这里发现孩子节点中5最小于是交换5和根节点的位置。对于右节点72 的字节点71,84 ,因为左节点71小于该节点72,于是交换72 节点和他的孩子中的最小值16 交换。完成最小堆的构建。

性能分析

对于最小堆(节点数n,根节点为0层,树的高度为h)：
- 第i层节点数最多为$frac{n+1}{2^{h-i}}$,以上面的例子来看：树的最大节点数n为15（将64，72，71 的叶子补齐）。高度h为4。最后一层的元素个数为(n+1)/2^{4-3}=8,导数第二层(n+1)/2^{4-2}=4
- 第i层所做操作最多为第i 层节点数乘上交换次数。比如例子中最后一层无需做任何交换，但是倒数第二层最多每个节点做一次交换，倒数第三层可能除了和倒数第二层交换后，交换到倒数第二层的元素可能还需要和倒数第一层的元素交换，这样需要两次交换。倒数第四层同样的道理需要3次交换。
i 层交换的次数为$2^i*(h-i-1)$,总的交换次数为:$sum_{i=0}^{h-2}2^i*(h-i-1)=$

$$begin{align*} sum_{i=0}^{h-2}2^i*(h-i-1)&=2^{0}(h-1)+2^{1}(h-2)+2^2(h-3)+ldots+2^{h-2}\ &=2^{h-2}(1+2cdot2^1+3cdot2^2+ldots+frac{h-2}{2^{h-3}}+frac{h-1}{2^{h-2}})\ &<2^{h-2}(1+2cdot2^1+3cdot2^2+ldots+frac{h-2}{2^{h-3}}+frac{h-1}{2^{h-2}}+frac{h}{2^{h-1}}+ldots)\ &=2^{h-2}frac{1}{(1-1/2)^2}=2^h=n end{align*}$$
如果往堆里面插入一个元素需要 $log_2(n)$ 次比较 n 个元素插入，删除时间 $nlog_2(n)+nlog_2(n)$为 $O(nlog(n))$
在上面的例子中总交换次数次数 $2^0cdot3+2^1cdot2+2^2cdot3$。
总共时间代价为建堆的时间代价 $O(nlog(n))$ 和交换的时间代价 $n$ 的总代价为$O(nlog_2(n))$

代码解析

下面的代码中排序只是一个简单的实现，主要是为了展现堆的数据结构和数组实现。
构造函数用一个MaxSize表示当前堆容纳的数组元素的最大数。CurrentSize是当前存放的数据的大小，heapArray存放待排序数据中的所有元素。

#include <iostream>
using namespace std;
class MinHeap{
private:
    int *heapArray;
    int CurrentSize;
    int MaxSize;
    void BuildHeap(int n);

public:
    MinHeap(const int n,const int *a);//构造函数实现创建一个n个元素的堆，最大容量为n+10
    virtual ~MinHeap();//析构函数
    bool isLeaf(int pos) const;//是不是叶子节点（在排序中没有用）但是应该作为堆的一部分才更完三
    int leftchild(int pos) const;//是不是左孩子，这里这个函数也不是必须，主要是用来确定孩子那个更小，将更小的向上siftup
    int parent(int pos) const;//获取当前位置的父节点
    bool Remove(int pos,int & node);//删除位置pos的元素给赋值给node
    bool Insert(const int &newNode);//插入newnode元素
    void RemoveMin(int &min_val);//删除堆的第一个元素（最小值）
    void SiftUp(int position);//向上交换
    void SiftDown(int position);//向下交换
    void show();//方便调试
    void sort();
};
MinHeap::MinHeap(const int n,const int *a) {
    CurrentSize = n;
    MaxSize = CurrentSize+10;
    heapArray = new int[MaxSize];
    int i=0;
    for(int i=0;i<n;i++)
        heapArray[i] = a[i];
    BuildHeap(CurrentSize);
}
MinHeap::~MinHeap() {
    delete [] heapArray;
}
void MinHeap::SiftDown(int position) {
    int i = position;
    int j = 2*i+1;
    int temp = heapArray[i];
    while(j<CurrentSize)
    {
        if(j<CurrentSize-1&&heapArray[j]>heapArray[j+1])
            j++;
        if(temp>heapArray[j])
        {
            heapArray[i] = heapArray[j];
            i = j;
            j = 2*j+1;
        }
        else
            break;
    }
    heapArray[i] = temp;
}
void MinHeap::BuildHeap(int n) {
    CurrentSize = n;
    for(int i=CurrentSize/2-1;i>=0;i--)
    {
        SiftDown(i);
    }
}
void MinHeap::SiftUp(int position) {
    int temppos = position;
    int temp = heapArray[temppos];
    while((temppos>0)&&(heapArray[parent(temppos)]>temp))
    {
        heapArray[temppos] = heapArray[parent(temppos)];
        temppos=parent(temppos);
    }
    heapArray[temppos] = temp;
}
bool MinHeap::Remove(int pos, int &node) {
    if((pos<0)||(pos>=CurrentSize))
        return false;
    int temp = heapArray[pos];
    heapArray[pos] = heapArray[--CurrentSize];
    if(heapArray[parent(pos)]>heapArray[pos])
        SiftUp(pos);
    else
        SiftDown(pos);
    node = temp;
    return true;
}
int MinHeap::parent(int pos) const {
    return pos/2;
}
void MinHeap::RemoveMin(int &min_val) {
    min_val = heapArray[0];
    for(int i=1;i<CurrentSize;i++)
        heapArray[i-1]=heapArray[i];
}
bool MinHeap::isLeaf(int pos) const {
    if(pos*2+1>=CurrentSize)
        return true;
    else
        return false;
}
int MinHeap::leftchild(int pos) const {
    if(pos*2+1<CurrentSize)
        return pos*2+1;
}
bool MinHeap::Insert(const int &newNode) {
    if(CurrentSize == MaxSize)
        return false;
    heapArray[CurrentSize] = newNode;
    SiftUp(CurrentSize);
    CurrentSize++;
}
void MinHeap::show() {
    for(int i=0;i<CurrentSize;i++)
        cout<<heapArray[i]<<" ";
    cout<<"n";
}
void MinHeap::sort() {
    int min_val;
    for(int i=CurrentSize;i>0;i--)
    {
        BuildHeap(i);
        RemoveMin(min_val);
        cout<<min_val<<" ";
    }
    cout<<"n";
}
int main()
{
    int a[] = {72,23,5,68,94,16,71,84,76};
    MinHeap m = MinHeap(9,a);
    m.Insert(63);
    m.show();
//    m.sort();
}

最后

以上就是友好手机为你收集整理的堆排序堆排序算法的全部内容，希望文章能够帮你解决堆排序堆排序算法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。