一，基本流程

决策树是一类常见的机器学习方法。一般的，一棵决策树包含一个根节点，若干个内部节点和若干个叶节点。叶节点对应于决策结果，其他每个节点则对应于一个属性测试；每个节点包含的样本集合根据属性测试的结果被划分到子节中；根节点包含样本全集。

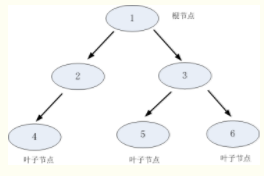
$\cdot$基本流程遵循“分而治之”策略。
树的构建流程;
步骤1：将所有的数据看成是一个节点（根节点），进入步骤2；
步骤2：根据划分准则，从所有属性中挑选一个对节点进行分割，进入步骤3；
步骤3：生成若干个子节点，对每一个子节点进行判断，如果满足停止分裂的条件，进入 步骤4；否则，进入步骤2；
步骤4：设置该节点是叶子节点，其输出的结果为该节点数量占比最大的类别。
注：在决策树基本算法中，有三种情形会导致递归返回:

1. 当前结点包含的样本全属于同一类别，无需划分;
2. 当前属性集为空，或是所有样本在所有属性上取值相同，无法划分;
3. 当前结点包含的样本集合为空，不能划分。

二，划分选择

决策树的关键在于如何划分最优化属性。一般而言，随着划分过程不断进行，希望决策树 的分支节点所包含的样本尽可能属于同一类别，即节点的“纯度”越来越高。

2.1信息增益

**”信息熵“**是度量样本集合纯度最常用的一种指标。假定当前样本集合$D$中第$k$类样本所占比例为$p_k(k=1,2,3,...,|y|)$,则$D$的信息熵定义为:

$Ent(D)=-{\sum }_{k=1}^{|y|}{p}_{k}lo{g}_2{p}_k$

$Ent(D)$值越小，则D的纯度越高
注：

1）约定p=0时，$plog(p)=0$；
2）当D只含一类时（纯度最高），此时Ent（D）=0（最小值）
3）当D中所有类所占比例相同（纯度最低），此时Ent（D）=（最大值）

计算熵的代码：

def calc_ent(x):
    """
        calculate shanno ent of x
    """

    x_value_list = set([x[i] for i in range(x.shape[0])])
    ent = 0.0
    for x_value in x_value_list:
        p = float(x[x == x_value].shape[0]) / x.shape[0]
        logp = np.log2(p)
        ent -= p * logp

    return ent

假定离散属性a有V个可能的取值{$a^1,a^2,...,a^v$},若使用a对样本集D进行划分，则会产生V个分支节点，其中第$v$个分支节点包含了D中所有在属性a上取值为$a^v$的样本，记为$D^v$。由上式可以加算出$D^v$信息熵。

再考虑到不同分支所包含的样本数不同，给分支节点赋予权重$|D^v|/|D|$,即样本数越多的分支节点所包含的分支节点影响较大，于是可以计算出属性a对样本集D进行划分所获得的”信息增益“

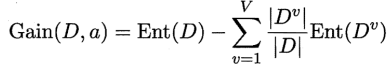
注：

1）一般而言，信息增益越大，则意味着用属性a来进行划分所获得的"纯度提升"越大，因此，我们可用信息增益来进行决策树的划分属性选择。
2）著名的ID3 决策树学习算就是以信息增益为准则来选择划分属性。

代码实现：

def calc_condition_ent(x, y):
    """
        calculate ent H(y|x)
    """

    # calc ent(y|x)
    x_value_list = set([x[i] for i in range(x.shape[0])])
    ent = 0.0
    for x_value in x_value_list:
        sub_y = y[x == x_value]
        temp_ent = calc_ent(sub_y)
        ent += (float(sub_y.shape[0]) / y.shape[0]) * temp_ent

    return ent
def calc_ent_grap(x,y):
    """
        calculate ent grap
    """

    base_ent = calc_ent(y)
    condition_ent = calc_condition_ent(x, y)
    ent_grap = base_ent - condition_ent

    return ent_grap

划分的依据就是比较数据集合的各个属性对应的信息增益，选择信息增益最大的就是最优解。

2.2增益率

实际上，信息增益准则对可取数目较多的属性有所偏好，为减少这种偏好可能带来的不利影响，C4.5算法不直接使用信息增益，而是使用”增益率“来选择最优划分属性

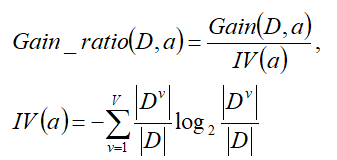
其中$IV(a)$称为属性a的”固有值“。属性a的可能取值数目越多，即V越大，则$IV(a)$的值通常会越大。
需要注意的是，增益率准则对可取值数目较少的属性有所偏好，因此C45算法斌不是直接选择增益率最大的候选划分属性，而是使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。
代码实现C45算法:

# -*- coding: utf-8 -*-
 
from numpy import *
import math
import copy
import cPickle as pickle
 
 
class C45DTree(object):
    def __init__(self):  # 构造方法
        self.tree = {}  # 生成树
        self.dataSet = []  # 数据集
        self.labels = []  # 标签集
 
 
    # 数据导入函数
    def loadDataSet(self, path, labels):
        recordList = []
        fp = open(path, "rb")  # 读取文件内容
        content = fp.read()
        fp.close()
        rowList = content.splitlines()  # 按行转换为一维表
        recordList = [row.split(",") for row in rowList if row.strip()]  # strip()函数删除空格、Tab等
        self.dataSet = recordList
        self.labels = labels
 
 
    # 执行决策树函数
    def train(self):
        labels = copy.deepcopy(self.labels)
        self.tree = self.buildTree(self.dataSet, labels)
 
 
    # 构件决策树：穿件决策树主程序
    def buildTree(self, dataSet, lables):
        cateList = [data[-1] for data in dataSet]  # 抽取源数据集中的决策标签列
        # 程序终止条件1：如果classList只有一种决策标签，停止划分，返回这个决策标签
        if cateList.count(cateList[0]) == len(cateList):
            return cateList[0]
        # 程序终止条件2：如果数据集的第一个决策标签只有一个，返回这个标签
        if len(dataSet[0]) == 1:
            return self.maxCate(cateList)
        # 核心部分
        bestFeat, featValueList= self.getBestFeat(dataSet)  # 返回数据集的最优特征轴
        bestFeatLabel = lables[bestFeat]
        tree = {bestFeatLabel: {}}
        del (lables[bestFeat])
        for value in featValueList:  # 决策树递归生长
            subLables = lables[:]  # 将删除后的特征类别集建立子类别集
            # 按最优特征列和值分隔数据集
            splitDataset = self.splitDataSet(dataSet, bestFeat, value)
            subTree = self.buildTree(splitDataset, subLables)  # 构建子树
            tree[bestFeatLabel][value] = subTree
        return tree
 
 
    # 计算出现次数最多的类别标签
    def maxCate(self, cateList):
        items = dict([(cateList.count(i), i) for i in cateList])
        return items[max(items.keys())]
 
 
    # 计算最优特征
    def getBestFeat(self, dataSet):
        Num_Feats = len(dataSet[0][:-1])
        totality = len(dataSet)
        BaseEntropy = self.computeEntropy(dataSet)
        ConditionEntropy = []     # 初始化条件熵
        slpitInfo = []    # for C4.5,caculate gain ratio
        allFeatVList = []
        for f in xrange(Num_Feats):
            featList = [example[f] for example in dataSet]
            [splitI, featureValueList] = self.computeSplitInfo(featList)
            allFeatVList.append(featureValueList)
            slpitInfo.append(splitI)
            resultGain = 0.0
            for value in featureValueList:
                subSet = self.splitDataSet(dataSet, f, value)
                appearNum = float(len(subSet))
                subEntropy = self.computeEntropy(subSet)
                resultGain += (appearNum/totality)*subEntropy
            ConditionEntropy.append(resultGain)    # 总条件熵
        infoGainArray = BaseEntropy*ones(Num_Feats)-array(ConditionEntropy)
        infoGainRatio = infoGainArray/array(slpitInfo)  # C4.5信息增益的计算
        bestFeatureIndex = argsort(-infoGainRatio)[0]
        return bestFeatureIndex, allFeatVList[bestFeatureIndex]
 
    # 计算划分信息
    def computeSplitInfo(self, featureVList):
        numEntries = len(featureVList)
        featureVauleSetList = list(set(featureVList))
        valueCounts = [featureVList.count(featVec) for featVec in featureVauleSetList]
        pList = [float(item)/numEntries for item in valueCounts]
        lList = [item*math.log(item, 2) for item in pList]
        splitInfo = -sum(lList)
        return splitInfo, featureVauleSetList
 
 
 # 计算信息熵
    # @staticmethod
    def computeEntropy(self, dataSet):
        dataLen = float(len(dataSet))
        cateList = [data[-1] for data in dataSet]  # 从数据集中得到类别标签
        # 得到类别为key、 出现次数value的字典
        items = dict([(i, cateList.count(i)) for i in cateList])
        infoEntropy = 0.0
        for key in items:  # 香农熵： = -p*log2(p) --infoEntropy = -prob * log(prob, 2)
            prob = float(items[key]) / dataLen
            infoEntropy -= prob * math.log(prob, 2)
        return infoEntropy
 
 
    # 划分数据集： 分割数据集； 删除特征轴所在的数据列，返回剩余的数据集
    # dataSet : 数据集； axis: 特征轴； value: 特征轴的取值
    def splitDataSet(self, dataSet, axis, value):
        rtnList = []
        for featVec in dataSet:
            if featVec[axis] == value:
                rFeatVec = featVec[:axis]  # list操作：提取0~（axis-1）的元素
                rFeatVec.extend(featVec[axis + 1:])   # 将特征轴之后的元素加回
                rtnList.append(rFeatVec)
        return rtnList
 
    # 存取树到文件
    def storetree(self, inputTree, filename):
        fw = open(filename,'w')
        pickle.dump(inputTree, fw)
        fw.close()
 
    # 从文件抓取树
    def grabTree(self, filename):
        fr = open(filename)
        return pickle.load(fr)

三，剪枝处理

剪枝(pruning)是决策树学习算法对付”过拟合“的主要手段。在决策树的学习中，为了尽可能正确分类训练集，节点划分过程将不断重复，有时会造成决策树分支过多，这时就可能因为训练样本”太好“，以至于把训练集自身的特点当作数据都具有的一般性质而导致过拟合。因此，可通过主动去掉分支来降低过拟合的风险。

决策树剪枝的基本策略有：”预剪枝“和”后剪枝“。预剪枝是指在决策树生成过程中，对每个节点在划分前进行估计，若当前节点的划分不能带来决策树泛化性能提升，则停止划分并将当前节点标记为叶节点；后剪枝则是先从训练集生成一棵完整的决策树，然后自底向上地对非叶节点进行考察，若将该节点对应的子树替换为叶节点能带来决策树泛化性能的提升，则将该子树替换成叶节点。

运用留出法评估决策树泛化性能的提升，利用西瓜数据集举例

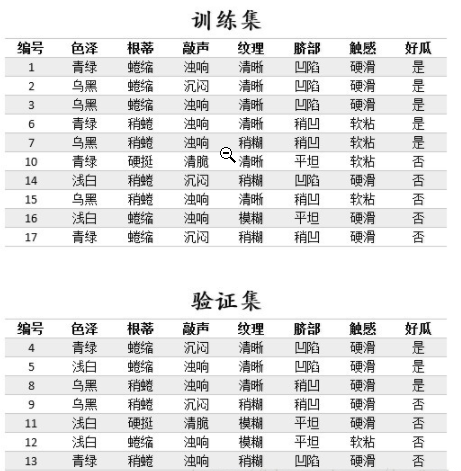
首先利用训练集数据，构造一个未做剪枝处理的决策树，以便于与剪枝后的决策树做对比。

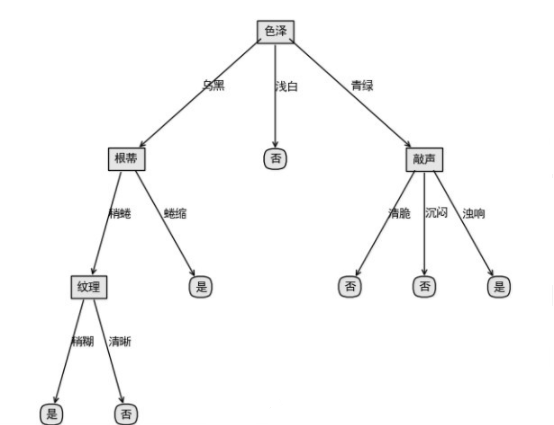
3.1 预剪枝

预剪枝的过程：
1）根据信息增益准则，选取“色泽”作为根节点进行划分，会产生3个分支（青绿、乌黑、浅白）。

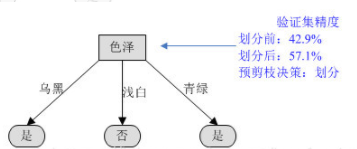
对根节点“色泽”，若不划分，该节点被标记为叶节点，训练集中正负样本数相等，我们将其标记为“是”好瓜（当样本最多的类不唯一时，可任选其中一类，我们默认都选正类）。那么训练集的7个样本中，3个正样本被正确分类，验证集精度为3/7100%=42.9%。
对根节点“色泽”划分后，产生图中的3个分支，训练集中的7个样本中，编号为{8,11,12,4}的4个样本被正确分类，验证集精度为4/7100%=57.1%。
于是节点“色泽”应该进行划分。

2）再看“色泽”为乌黑这个分支，如果对其进行划分，选择“根蒂”作为划分属性

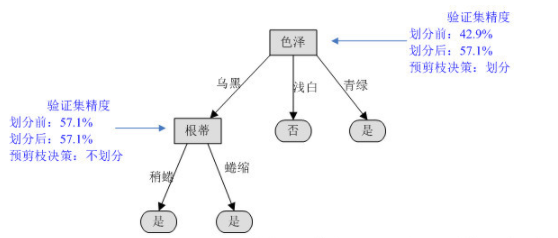
对“根蒂”这个分支节点，如果不划分，验证集精度为57.1%。如果划分，进入此分支的两个样例{8,9}，编号为8的样例分类正确，编号为9的样例分类错误，所以对整棵树来说编号为{4,8,11,12}的4个样本分类正确，验证集精度仍为57.1%。
按预剪枝的策略，验证集精度没有提升的话，不再划分。

3）“色泽”为浅白的分支只有一个类别，无法再划分。再评估“色泽”为青绿的分支，如果对其进行划分，选择“敲声”作为划分sh属性，产生3个分支。

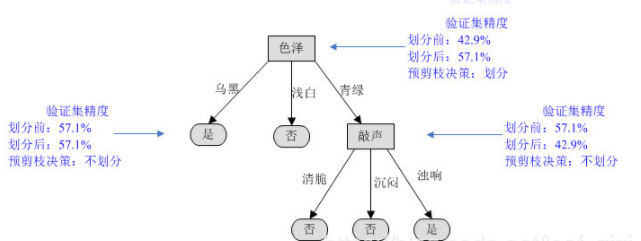
对“敲声”这个分支节点，如果不划分，验证集精度为57.1%。如果划分，进入此分支的两个样例{4,13}，编号为4的样例分类错误，编号为13的样例也分类错误，所以对整棵树来说编号为{8,11,12}的4个样本分类正确，验证集精度仍为42.9%。
按预剪枝的策略，验证集精度没有提升的话，不再划分。
因此，通过预剪枝处理生成的树只有一个根节点，这种树也称“决策树桩”。

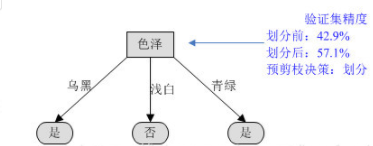
优缺点分析：预剪枝使得决策树的很多分支没有展开，可以降低过拟合的风险，减少决策树的训练时间和测试时间。但是，尽管有些分支的划分不能提升泛化性能，但是后续划分可能使性能显著提高，由于预剪枝没有展开这些分支，带来了欠拟合的风险。

3.2 后剪枝

后剪枝是在决策树构造完成后，自底向上对非叶节点进行评估，为了方便分析，我们对树中的非叶子节点进行编号，然后依次评估其是否需要剪枝。

对于完整的决策树，在剪枝前，编号为{11，12}的两个样本被正确分类，因此其验证集精度为2/7*100%=28.6%。

（1）第一步先考察编号为4的结点，如果剪掉该分支，该结点应被标记为“是”。进入该分支的验证集样本有{8,9}，样本8被正确分类，对整个验证集，编号为{8,11,12}的样本正确分类，因此验证集精度提升为42.9%，决定剪掉该分支。

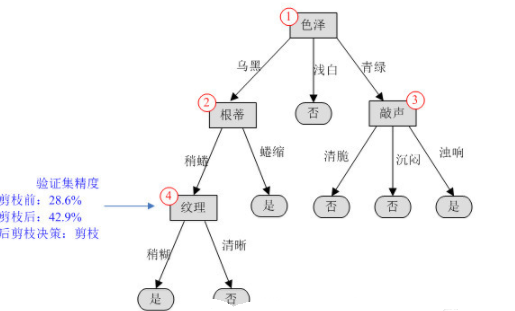
（2）再来考察编号为3的结点，如果剪掉该分支，该结点应标记为“是”，进入该分支的样本有{4,13}，其中样本4被正确分类，对整个验证集，编号为{4,8,11,12}的样本正确分类，因此验证集精度提升为57.1%，决定剪掉该分支。

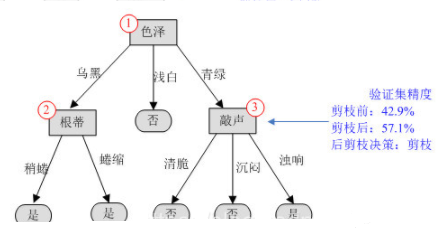
（3）再看编号为2的结点，如果剪掉该分支，该结点应标记为“是”，进入该分支的样本有{8,9}，其中样本8被正确分类，样本9被错误分类，对整个验证集，编号为{4,8,11,12}的样本正确分类，验证集精度仍为57.1%，没有提升，因此不做剪枝。

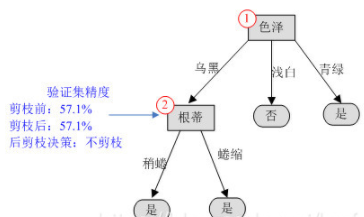
（4）对编号为1的结点，如果对其剪枝，其验证集精度为42.9%（同预剪枝的第一步），因此也不剪枝。
后剪枝得到的决策树就是第（3）步的样子。

优缺点分析：后剪枝通常比预剪枝保留更多的分支，欠拟合风险小。但是后剪枝是在决策树构造完成后进行的，其训练时间的开销会大于预剪枝。

由于后剪枝的泛化能力高于预剪枝，这里只对后剪枝编程。

def postPruningTree(inputTree, dataSet, data_test, labels, labelProperties):
    """ 
    type: (dict, list, list, list, list) -> dict
    inputTree: 已构造的树
    dataSet: 训练集
    data_test: 验证集
    labels: 属性标签
    labelProperties: 属性类别
    """
    firstStr = inputTree.keys()[0]
    secondDict = inputTree[firstStr]
    classList = [example[-1] for example in dataSet]
    featkey = copy.deepcopy(firstStr)
    if '<' in firstStr:  # 对连续的特征值，使用正则表达式获得特征标签和value
        featkey = re.compile("(.+<)").search(firstStr).group()[:-1]
        featvalue = float(re.compile("(<.+)").search(firstStr).group()[1:])
    labelIndex = labels.index(featkey)
    temp_labels = copy.deepcopy(labels)
    temp_labelProperties = copy.deepcopy(labelProperties)
    if labelProperties[labelIndex] == 0:  # 离散特征
        del (labels[labelIndex])
        del (labelProperties[labelIndex])
    for key in secondDict.keys():  # 对每个分支
        if type(secondDict[key]).__name__ == 'dict':  # 如果不是叶子节点
            if temp_labelProperties[labelIndex] == 0:  # 离散的
                subDataSet = splitDataSet(dataSet, labelIndex, key)
                subDataTest = splitDataSet(data_test, labelIndex, key)
            else:
                if key == 'yes':
                    subDataSet = splitDataSet_c(dataSet, labelIndex, featvalue,
                                               'L')
                    subDataTest = splitDataSet_c(data_test, labelIndex,
                                                featvalue, 'L')
                else:
                    subDataSet = splitDataSet_c(dataSet, labelIndex, featvalue,
                                               'R')
                    subDataTest = splitDataSet_c(data_test, labelIndex,
                                                featvalue, 'R')
            inputTree[firstStr][key] = postPruningTree(secondDict[key],
                                                       subDataSet, subDataTest,
                                                       copy.deepcopy(labels),
                                                       copy.deepcopy(
                                                           labelProperties))
    if testing(inputTree, data_test, temp_labels,
               temp_labelProperties) <= testingMajor(majorityCnt(classList),
                                                     data_test):
        return inputTree
    return majorityCnt(classList)

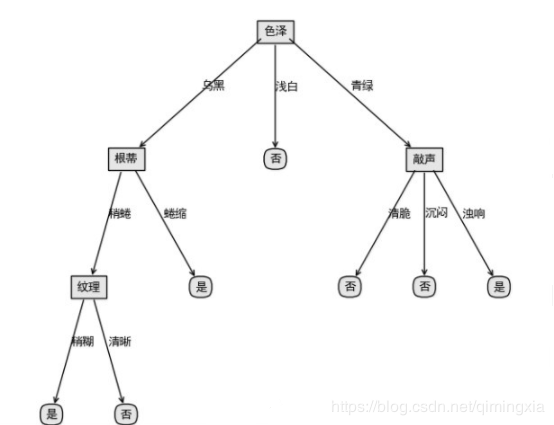
运行程序绘制出剪枝后的决策树，与上面人工绘制的一致。

最后

以上就是粗犷大叔为你收集整理的机器学习———决策树一，基本流程二，划分选择三，剪枝处理的全部内容，希望文章能够帮你解决机器学习———决策树一，基本流程二，划分选择三，剪枝处理所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。