1. 首页
  2. 文章中心
  3. 机器学习课程作业

作业1：ID3 算法实验报告作业1：ID3 算法实验报告

84 阅读 0 评论
我是靠谱客的博主 魁梧纸鹤，最近开发中收集的这篇文章主要介绍作业1：ID3 算法实验报告作业1：ID3 算法实验报告，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

作业1：ID3 算法实验报告

1. 算法介绍

信息增益：特征 A 对训练数据集 D 的信息增益 g(D, A)，定义为集合 D 的经验熵 H(D) 与特征 A 给定条件下 D 的讲演条件熵 H(D|A) 之差，即 g(D, A) = H(D) - H(D|A)。

ID3 算法的核心实在决策树各个节点上应用信息增益准则选择特征，递归地构建决策树。具体方法是：从根结点（root node）开始，对节点计算所有可能特征的信息增益，选择信息增益最大的特征作为结点的特征，由该特征的不同取值构建子结点；再对子结点递归调用上述方法，构建决策树；知道所有特征的信息增益均很小或没有特征可以选择为止。最后得到一个决策树。ID3 算法相当于用最大似然法进行概率模型的选择。

2. 算法流程

算法如下：

  • input：训练数据集D，特征集A，阈值ε；

  • output：决策树T。

  1. 若 D 中所有实例属于同一类 Ck，则 T 为单结点树，并将类 Ck 作为该结点的类标记，返回 T；

  2. 若 A=Φ ，则 T 为单结点树，并将 D 中实例数最大的类 Ck 作为改结点的类标记，返回 T；

  3. 否则，计算 A 中各特征对 D 的信息增益，选择信息增益最大的特征 Ag；

  4. 如果 Ag 的信息增益小于阈值 ε，则置 T 为单结点树，并将 D 中实例数最大的类 Ck 作为该结点的类标记，返回 T；

  5. 否则，对 Ag 的每一个可能值 ai，依 Ag=ai 将 D 分割为若干空子集 Di，将 Di 中实例数最大的类 Ck 作为标记，构建子结点，由结点及其子结点构成树 T，返回 T；

  6. 对第 i 个子结点，以 Di 为训练集，以 A-{Ag} 为特征集，递归地调用步骤1~5，得到子树 Ti，返回 Ti。

3. 数据集介绍

DNA 数据集（STATLOG 版本）——灵长类剪接基因序列（DNA）与相关的不完善域理论。

剪接接头是DNA序列上的点，在高等生物的蛋白质生成过程中，多余的DNA会在此处被去除。该数据集中提出的问题是，在给定DNA序列的情况下，识别外显子(剪接后保留的DNA序列部分)和内含子(剪接后的DNA序列部分)之间的边界。这个问题由两个子任务组成:识别外显子/内含子边界(简称EI位点)，识别内含子/外显子边界(IE位点)(在生物学界，IE边界被称为“受体”，而EI边界被称为“供体”)。

StaLog dna 数据集是下面描述的Irvine数据库的一个经过处理的版本。主要区别是代表核苷酸的符号变量(只有A，G，T，C)被3个二元指示变量代替。因此，最初的60个符号属性变成了180个二进制属性。示例的名称已被删除。有歧义的例子被删除了(很少，4)。这个数据集的统计版本是由拉斯克莱德大学的罗斯·金制作的。如需原始详细信息，请参阅Irvine数据库文档。

核苷酸A、C、G、T的指示值如下：

A -> 1 0 0
C -> 0 1 0
G -> 0 0 1
T -> 0 0 0

ei 表示供体；ie 表示受体；n 表示两种都不是。指示值如下：

ei -> 1
ie -> 2
n  -> 3

研究结果表明，机器学习技术(神经网络、最近邻、贡献者KBANN系统)的性能与基于典型模式匹配的分类(生物文献中使用的方法)相当/更好。开发此数据集是为了帮助评估“混合”学习算法(KBANN)，该算法使用示例来归纳提炼已有知识。对从3190个完整样本中随机抽取的1000个样本采用“十重交叉验证”方法，通过各种ML算法得出以下错误率(所有实验均在威斯康星大学进行，有时采用已发表算法的本地实现)。

4. 算法实现过程

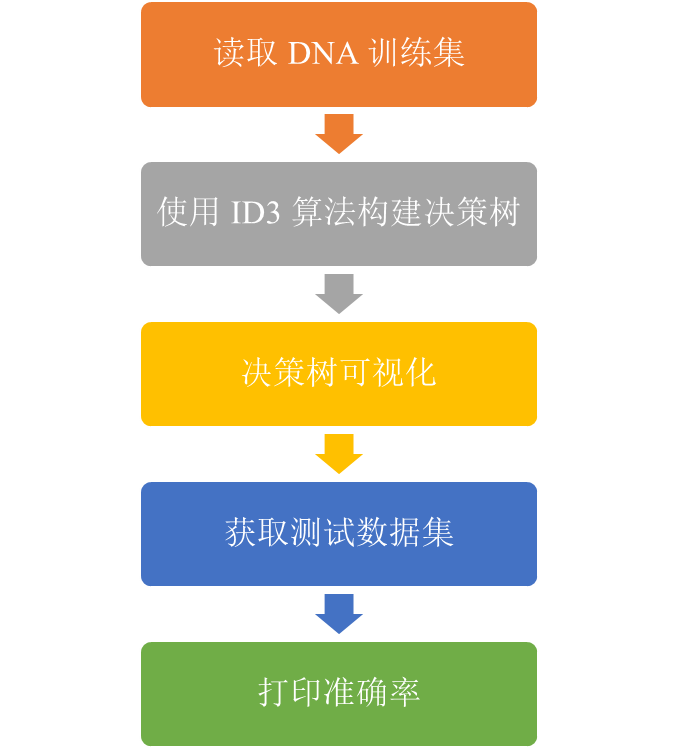
在这里插入图片描述

4.1. 读取 DNA 训练集

DNA 数据集中有 180 个属性，与之对应定义一个 labels，用来保存这些属性（A0~A179）。然后利用 Python 中的文件读取方法将数据集读取到 dataSet，最后将定义好的标签和保存的数据集返回。

def creatDataSetDNA():
    dataSet = []
    labels = []
    # 创建标签，A0-A179，共180个
    for i in range(180): labels.append(str('A' + str(i)))
    # 读取数据
    with open("../ID3算法/dna.data", "r", encoding="utf-8") as f:
        for line in f:
            # 只获取数字，并除去空格，然后转化为list
            strList = line[:-2].split(' ')
            # 将 str list 转为 int list，并加入 dataSet
            dataSet.append(list(map(int, strList)))
    return dataSet, labels

4.2. 使用 ID3 算法构建决策树

4.2.1. 计算香农熵

熵表示随机变量不确定性的度量。首先给所有可能分类创建字典，然后以 2 为底数计算香农熵，最后返回香农熵。

  1. 给所有可能分类创建字典
for featVec in dataSet:
    currentLabel = featVec[-1]
    if currentLabel not in labelCounts.keys():
        labelCounts[currentLabel] = 0
    labelCounts[currentLabel] += 1
  1. 以 2 为底数计算香农熵
for key in labelCounts:
    prob = float(labelCounts[key]) / numEntrtries
    shannonEnt -= prob * math.log(prob, 2)

4.2.2. 离散变量划分数据集

取出该特征取值为value的所有样本。

def splitDataSet(dataSet, axis, value):
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]
            reducedFeatVec.extend(featVec[axis + 1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet

4.2.3. 选择最好的数据集划分方式

定义列表 featList 用来保存数据集中每一列的所有值，然后调用 set() 方法保证集合中每个值互不相同，接着计算信息增益，即熵的减少，保存信息增益最大的特征。最后将划分好的数据集返回。

for i in range(numFeatures):
    featList = [example[i] for example in dataSet]
    uniqueVals = set(featList)
    newEntropy = 0.0
    for value in uniqueVals:
        subDataSet = splitDataSet(dataSet, i, value)
        prob = len(subDataSet) / float(len(dataSet))
        newEntropy += prob * calcShannonEnt(subDataSet)
    infoGain = baseEntropy - newEntropy
    if infoGain > bestInfoGain:
        bestInfoGain = infoGain
        bestFeature = i
return bestFeature

4.2.4. 投票决定分类

当所有的特征都用完的时候，需要使用投票机制来决定分类情况：

def majorityCnt(classList):
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

4.3. 决策树可视化

4.3.1. 定义文本框和箭头格式

decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")

4.3.2. 获取叶子结点数目

keys函数是Python的字典函数，它返回字典中的所有键所组成的一个可迭代序列。使用keys()可以获得字典中所有的键。

firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
    # 是字典继续递归，不是字典就是叶节点
    if type(secondDict[key]).__name__ == "dict":
        numLeafs += getNumLeafs(secondDict[key])
    else:
        numLeafs += 1
return numLeafs

4.3.3. 计算树的最大深度

for key in secondDict.keys():
    if type(secondDict[key]).__name__ == "dict":
        thisDepth = 1 + getTreeDepth(secondDict[key])
    else:
        thisDepth = 1
    if thisDepth > maxDepth:
        maxDepth = thisDepth
return maxDepth

4.3.4. 画箭头上的文字

def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
    yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
    createPlot.axl.text(xMid, yMid, txtString)

4.3.5. 画决策树

 for key in secondDict.keys():
    if type(secondDict[key]).__name__ == 'dict':
        plotTree(secondDict[key], cntrPt, str(key))
    else:
        plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
        plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
        plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD

4.4. 获取测试数据集

这个方法与读取 DNA 训练集的方法比较类似：

def getTestData():
    testData = []
    with open("../ID3算法/dna.test", "r", encoding="utf-8") as f:
        for line in f:
            testData.append(list(map(int, line[:-2].split(' '))))
    return testData

4.5. 实验结果

4.5.1. 决策树显示

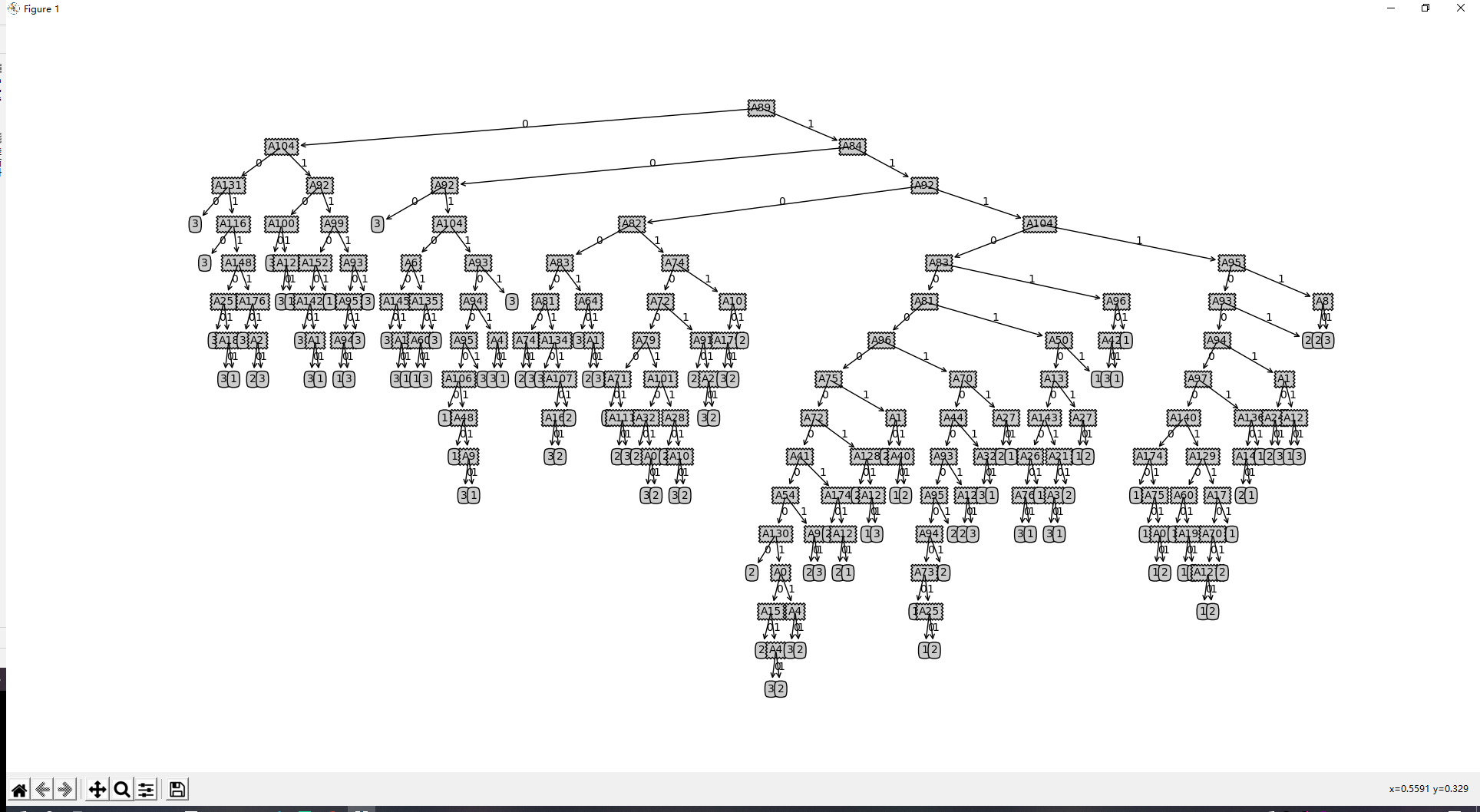
在这里插入图片描述

4.5.2. 准确率

  1. 对一项测试数据进行预测，通过递归来预测该项数据的标签。
 if one_test_data[attribute_index] == key:
    if type(second_dic[key]).__name__ == 'dict':
        res_label = decision_tree_predict(second_dic[key], attribute_labels, one_test_data)
    else:
        res_label = second_dic[key]
  1. 计算准确率：
totalNum, correctNum = {1: 0, 2: 0, 3: 0}, {1: 0, 2: 0, 3: 0}
    for data in testData:
        totalNum[data[-1]] += 1
        if decision_tree_predict(myTree, labels, data) == data[-1]:
            correctNum[data[-1]] += 1
    return correctNum[1] / totalNum[1], correctNum[2] / totalNum[2], correctNum[3] / totalNum[3], sum(list(correctNum.values())) / len(testData)
  1. 准确率输出结果：
    在这里插入图片描述

5. 总结

决策树是一种类似于流程图的树结构，由内部结点、叶节点、有向边组成。一个内部结点表示一个特征上的测试，一个叶节点表示类别标号。决策树分类就是从根节点开始，对实例的某一特征进行测试，根据测试结果将实例划分子节点，再对子结点上的剩余特征进行递归测试并分配，直到产生叶子节点。

ID3 算法优点：

  • 创建决策规则的过程简单。
  • 决策树可以可视化，输出结果易于理解。
  • 可以处理连续性和离散性数据。
  • 可用于分类和回归。

ID3 算法缺点：

  • 容易产生过拟合，可以通过剪枝来缓解。
  • 不能保证建立全局最优的决策树，可以通过随机森林来缓解。
    类似于流程图的树结构，由内部结点、叶节点、有向边组成。一个内部结点表示一个特征上的测试，一个叶节点表示类别标号。决策树分类就是从根节点开始，对实例的某一特征进行测试，根据测试结果将实例划分子节点，再对子结点上的剩余特征进行递归测试并分配，直到产生叶子节点。

ID3 算法优点：

  • 创建决策规则的过程简单。
  • 决策树可以可视化，输出结果易于理解。
  • 可以处理连续性和离散性数据。
  • 可用于分类和回归。

ID3 算法缺点：

  • 容易产生过拟合，可以通过剪枝来缓解。
  • 不能保证建立全局最优的决策树，可以通过随机森林来缓解。

最后

以上就是魁梧纸鹤为你收集整理的作业1：ID3 算法实验报告作业1：ID3 算法实验报告的全部内容，希望文章能够帮你解决作业1：ID3 算法实验报告作业1：ID3 算法实验报告所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(56)

相关文章

决策树学习心得
决策树学习心得
决策树（Decision Tree）原理小结1. 决策树2. ID3算法3. C4.5算法4. 剪枝算法5. CART算法6. 决策树延伸7. 决策树算法总结8. 决策树使用Demo完整代码参考
决策树（Decision Tree）原理小结1. 决策树2. ID3算法3. C4.5算法4. 剪枝算法5. CART算法6. 决策树延伸7. 决策树算法总结8. 决策树使用Demo完整代码参考
基于海思3559A方案+Atlas 200 AI模块_边缘计算平台开发及接口定义
基于海思3559A方案+Atlas 200 AI模块_边缘计算平台开发及接口定义
决策树原理总结决策树原理总结
决策树原理总结决策树原理总结
作业1：ID3 算法实验报告作业1：ID3 算法实验报告
作业1：ID3 算法实验报告作业1：ID3 算法实验报告
台湾联咏对标海思AI+IPC芯片规格对比列表
台湾联咏对标海思AI+IPC芯片规格对比列表
实验3 决策树 实操项目1：肿瘤预测（决策树）实验3 决策树 实操项目1：肿瘤预测（决策树）【实验内容】【实验要求】
实验3 决策树 实操项目1：肿瘤预测（决策树）实验3 决策树 实操项目1：肿瘤预测（决策树）【实验内容】【实验要求】
安霸Ambarella_CV2X_SOC_PLATFORM_海思AI方案的强力竞争对手
安霸Ambarella_CV2X_SOC_PLATFORM_海思AI方案的强力竞争对手

评论列表共有 0 条评论

立即
投稿
返回
顶部