机器学习之决策树——学习总结

决策树学习总结

机器学习的应用越来越广泛，特别是在数据分析领域。本文是我学习决策树算法的一些总结。

机器学习简介

机器学习 (Machine Learning) 是近 20 多年兴起的一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。简而言之，机器学习是通过学习老知识（训练样本），得出自己的认知（模型），去预测未知的结果。

• 学习方式
  
  • 监督式学习
    
    • 从给定的训练数据集中学习出一个函数，当新的数据到来时，可以根据此函数预测结果。训练数据集中的目标由人标注的。常见的算法有回归分析和统计分类
  • 非监督式学习
    
    • 与监督式学习相比，训练集没有人为标注的结果，常见的算法有聚类
  • 半监督式学习
    
    • 训练集部分被标识，部分没有被标识。常见的算法有SVM
  • 强化学习
    
    • 输入数据作为模型的反馈，模型对此作出调整。常见的算法有时间差学习
• 机器学习算法分类
  
  • 决策树算法
    
    • 根据数据属性，采用树状结构建立决策模型。常用来解决分类和回归问题。
    • 常见算法：CART(Classification And Regression Tree)，ID3，C4.5，随机森林等
  • 回归算法
    
    • 对连续值预测，如逻辑回归LR等
  • 分类算法
    
    • 对离散值预测，事前已经知道分类，如k-近邻算法
  • 聚类算法
    
    • 对离散值预测，事前对分类未知，如k-means算法
  • 神经网络
    
    • 模拟生物神经网络，可以用来解决分类和回归问题
    • 感知器神经网络(Perceptron Neural Network) ，反向传递(Back Propagation)和深度学习（DL）
  • 集成算法
    
    • 集成几种学习模型进行学习，将最终预测结果进行汇总
    • Boosting、Bagging、AdaBoost、随机森林 (Random Forest) 等

决策树算法

• 初识决策树
  决策树算法是借助于树的分支结构实现分类。以相亲约会决策为例，下图是建立好的决策树模型，数据的属性有4个：年龄、长相、收入、是否公务员，根据此模型，可以得到最终是见或者不见。
  
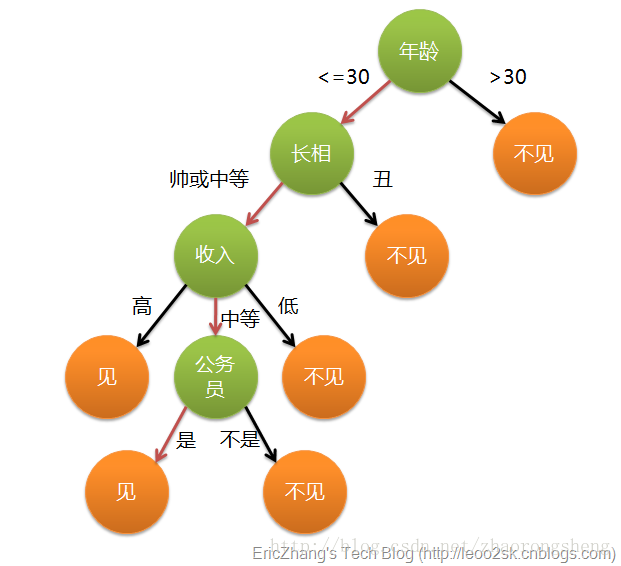
  这样，我们对决策树有个初步认识：

  • 叶子节点：存放决策结果
  • 非叶子节点：特征属性，及其对应输出，按照输出选择分支
  • 决策过程：从根节点出发，根据数据的各个属性，计算结果，选择对应的输出分支，直到到达叶子节点，得到结果

• 构建决策树
  通过上述例子，构建过程的关键步骤是选择分裂属性，即年龄、长相、收入、公务员这4个属性的选择先后次序。分裂属性是在某个节点处按照某一特征属性的不同划分构造不同的分支，其目标是让各个分裂子集尽可能的“纯”，即每个子集尽量都属于同一分类项。分裂属性分3种情况：

  • 属性是离散值且不要求生成二叉树
    
    • 属性的每个值作为一个分支
  • 属性是离散值且要求生成二叉树
    
    • 按照“属于”和“不属于”分成2个分支
  • 属性是连续值
    
    • 确定一个分裂点split_point，按照>split_point和<=split_point生成2个分支

  注意，决策树使用自顶向下递归分治法，并采用不回溯的贪心策略。分裂属性的选择算法很多，这里介绍3种常用的算法：信息增益（Information gain）、增益比率（gain ratio）、基尼指数（Gini index）

• 信息增益（Information Gain）
  基于香浓的信息论，信息熵表示不确定度，均匀分布时，不确定度最大，此时熵就最大。当选择某个特征对数据集进行分类时，数据集分类后的信息熵会比分类前的小，其差值即为信息增益。信息增益可以衡量某个特征对分类结果的影响大小，越大越好。
  
  • 典型算法：ID3
  • 数据集D中，有m个类别，( p_i )表示D中属于类别i的概率，此数据集的信息熵定义为： $$Info(D)=-sum_{i=1}^{m}p_ilog_2(p_i)$$
  • 以属性R作为分裂属性，R有k个不同的取值，将数据D划分成k组，按R分裂后的数据集的信息熵为： $$Info_R(D)=sum_{j=1}^{k}frac{|D_j|}{|D|}times Info(D_j)$$
  • 信息增益，即为划分前后，信息熵之差： $$Gain(R)=Info(D)-Info_R(D)$$
  • 在每层分裂时，选择使得Gain(R)最大的属性作为分裂属性
  • 缺点：此公式偏向数据量多的属性，如果样本分布不均，则会导致过拟合。假如上述例子中包括人名属性，每个人名均不同，显然以此属性作为划分，信息增益最高，但是，很明显，以此属性作为划分毫无意义
• 信息增益比率（Gain Ratio）
  针对上述方法问题，此方法引入分裂信息 $$SplitInfo_R(D)=-sum_{j=1}^{k}frac{|D_j|}{D}times log_{2}(frac{|D_j|}{D}))$$
  
  • 典型算法：C4.5
  • 信息增益比率定义为： $$GainRatio(R)=frac{Gain(R)}{SplitInfo_R(D)}$$
  • 缺点：( SplitInfo_R(D) )可能取值为0，此时无意义；当期趋于0时，GainRatio也不可信，改进措施是在分母加一个平滑，这里加所有分裂信息的平均值( GainRatio(R)=frac{Gain(R)}{overline{SplitInfo(D)}+SplitInfo_R(D)} )
• 基尼指数（Gini index）
  另外一种数据不纯度的度量方法，定义为： $$Gini(D)=1-sum_{i=1}^{m}{p_{i}}^{2}$$
  其中，m为数据集D中类别的个数，( p_i )表示D中属于类别i的概率，如果所有记录都属于同一个类中，则P1=1，Gini(D)=0。
  
  • 典型算法：CART
  • 以属性R作为分裂属性，R有k个不同的取值，将数据D划分成k组，按R分裂后的数据集的基尼指数为： $$Gini_R(D)=sum_{i=1}^{k}frac{|D_i|}{|D|}Gini(D_i)$$
  • 计算划分前后基尼指数之差 $$bigtriangleup Gini(R)=Gini(D)-Gini_R(D)$$ 计算Gini(R)增量最大的属性作为最佳分裂属性。

spark中实现

具体代码参考spark源码包下的org.apache.spark.examples.mllib.DecisionTreeClassificationExample，DecisionTree.trainClassifier的实现步骤，核心代码在RandomForest.run()方法

• 根据输入数据，构建RDD[LabeledPoint]，保存label和features
• 根据数据，构建metaData，包括feature个数、样本数据条数、分类个数等
  
  • val metadata =
DecisionTreeMetadata.buildMetadata(retaggedInput, strategy, numTrees, featureSubsetStrategy)
• 计算每个feature的可能划分点split1、split2。。。split(n-1)划分成n个bin
  
  • val splits = findSplits(retaggedInput, metadata, seed)
  • 连续值：取样数据，根据不同值个数和步长进行划分
  • 离散：
    
    • unorder：特征种类为binsNum（分类个数不大，且为多分类）
    • order：回归、二分类、多分类且数量很大，都使用二分类
• 根据feature的split，计算每条数据在每个feature下所在的bin，生成新的RDD[TreePoint(Label, featuresBin[])]
  
  • val treeInput = TreePoint.convertToTreeRDD(retaggedInput, splits, metadata)
• bagging取样（示例中，不需要取样，因为只生成一个tree）
  
  • val baggedInput = BaggedPoint
.convertToBaggedRDD(treeInput, strategy.subsamplingRate, numTrees, withReplacement, seed)
.persist(StorageLevel.MEMORY_AND_DISK)
• 新建树根root，放到queue中，循环直到队列为空
  
  • 选择多个训练树节点，同时进行训练，根据指定的maxMemoryUsage进行个数计算
    
    • val (nodesForGroup, treeToNodeToIndexInfo) =
RandomForest.selectNodesToSplit(nodeQueue, maxMemoryUsage, metadata, rng)
  • 按照Gini系数，找到当前树节点中，最佳的feature分裂点和最佳bin分割点
    
    • RandomForest.findBestSplits(baggedInput, metadata, topNodes, nodesForGroup,
treeToNodeToIndexInfo, splits, nodeQueue, timer, nodeIdCache)
    • 遍历数据，mapPartition，每个树节点LearnNode维护一个DTStatsAggregator（存放，每个feature的每个bin的数据个数）
    • 进行DTStatsAggregator的聚合merge
    • 按照Gini系数，找到最佳的feature下的最佳split

参数设置

可以通过设置一些参数，调整算法或调优，详细参考spark官网介绍

• 算法设置
  
  • algo：决策树类型，分类或回归，Classification or Regression
  • numClasses： 分类问题设置分类个数
  • categoricalFeaturesInfo：指定哪些feature是离散值，并指定离散值的个数
• 停止条件设置
  
  • maxDepth：树最大深度
  • minInstancesPerNode：每个树节点最小的训练数据个数，如果小于此值，则不进行分裂
  • minInfoGain：最小信息增益，决定当前树节点是否进行分裂
• 调优参数
  
  • maxBins：用于连续特征值的分散化，最多划分类个数
  • maxMemoryInMB：增大，可以提高同时训练的树节点的个数，从而减少训练时间，但是，每次训练会增大数据的传输量
  • subsamplingRate：训练森林时使用，每次采样的比例
  • impurity：纯度度量函数，必须和算法algo相匹配

参考文档

• 决策树算法介绍及应用
• 数据挖掘系列（6）决策树分类算法
• wikipedia_decisiontree

最后

以上就是野性鞋子为你收集整理的机器学习之决策树——学习总结的全部内容，希望文章能够帮你解决机器学习之决策树——学习总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。