1. 首页
  2. 文章中心
  3. 算法

6轴机器人运动学（正解）理论部分

310 阅读 0 评论
我是靠谱客的博主 醉熏小霸王，这篇文章主要介绍6轴机器人运动学（正解）理论部分，现在分享给大家，希望可以做个参考。

理论部分


概念

运动学正解，简而言之，就是给出6个关节变量，求得机械臂末端的位置和姿态
即给出 j 1 − j 6 j_1 - j_6 j1​−j6​，求 x , y , z , r x , r y , r z x,y,z,rx,ry,rz x,y,z,rx,ry,rz


DH参数

只单一地给出关节值或直角坐标值，是不能直接互相转化的，还与具体的机器人有关，这部分有关的内容可以用DH参数表来表示，其描述了机器人各关节坐标系之间的关系


表中内容
连杆长度 (length) ：2个相邻关节轴线之间的距离
连杆扭角 (angle) ：2个相邻关节轴线之间的角度
连杆偏距 (d) ：2个关节坐标系的X轴之间的距离


eg：UR5e

  • DH参数表
关节编号legth(mm)d(mm)angle(deg)
10162.590
2-42500
3-392.200
40133.390
5099.7-90
6099.60


计算

根据DH参数表以及 j 1 − j 6 j_1 - j_6 j1​−j6​，建立6个关节矩阵 A 1 − A 6 A_1-A_6 A1​−A6​，计算出转换矩阵 T 1 − T 6 T_1-T_6 T1​−T6​，计算 A 1 − A 6 A_1-A_6 A1​−A6​相乘得到矩阵R
R = [ r o t 3 ∗ 3 P 3 ∗ 1 0 1 ∗ 3 1 ] R=begin{bmatrix} {rot_{3*3}}&{P_{3*1}}\ {0_{1*3}}&{1}\ end{bmatrix} R=[rot3∗3​01∗3​​P3∗1​1​]
P 3 ∗ 1 = ( x , y , z ) T P_{3*1}=(x,y,z)^T P3∗1​=(x,y,z)T
则求出R即求出x,y,z
关节矩阵 A i A_i Ai​由当前的关节的 j i j_i ji​和DH参数导出
设当前 j i j_i ji​为 β beta β,legth为 l l l,d为 d d d,angle为 α alpha α
A i = [ c o s β − s i n β c o s α s i n β s i n α l c o s β s i n β c o s β c o s α − c o s β s i n α l s i n β 0 s i n α c o s α d 0 0 0 1 ] A_i= left[ begin{matrix} cosbeta & -sinbeta cosalpha & sinbeta sinalpha & lcosbeta \ sinbeta & cosbeta cosalpha & -cosbeta sinalpha & lsinbeta \ 0 & sinalpha & cosalpha & d \ 0 & 0 & 0 & 1 end{matrix} right] Ai​=⎣ ⎡​cosβsinβ00​−sinβcosαcosβcosαsinα0​sinβsinα−cosβsinαcosα0​lcosβlsinβd1​⎦ ⎤​
R = A 1 A 2 A 3 A 4 A 5 A 6 R=A_1A_2A_3A_4A_5A_6 R=A1​A2​A3​A4​A5​A6​


然后再求rx,ry,rz
r o t 3 ∗ 3 = [ r 00 r 01 r 02 r 10 r 11 r 12 r 20 r 21 r 22 ] rot_{3*3}= left[ begin{matrix} r_{00} & r_{01} & r_{02} \ r_{10} & r_{11} & r_{12} \ r_{20} & r_{21} & r_{22} \ end{matrix} right] rot3∗3​=⎣ ⎡​r00​r10​r20​​r01​r11​r21​​r02​r12​r22​​⎦ ⎤​
r x = a r c t a n ( r [ 1 ] [ 2 ] , r [ 2 ] [ 2 ] ) rx = arctan(r[1][2], r[2][2]) rx=arctan(r[1][2],r[2][2])
r y = a r c t a n ( r [ 0 ] [ 2 ] , r [ 0 ] [ 0 ] 2 + r [ 0 ] [ 1 ] 2 ) ry = arctan(r[0][2], sqrt{r[0][0] ^2 + r[0][1]^2}) ry=arctan(r[0][2],r[0][0]2+r[0][1]2 ​)
r z = a r c t a n ( r [ 0 ] [ 1 ] , r [ 0 ] [ 0 ] ) rz = arctan(r[0][1], r[0][0]) rz=arctan(r[0][1],r[0][0])

代码（C++）

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
/* 6轴机器人运动正解
 * 关节角度在文件我放在"D:\j.txt"中
 * 机器人参数在文件"D:\dh.txt"中
 * x,y,z,rx,ry,rz在屏幕输出 
 * 原代码来自https://blog.csdn.net/weixin_37942267/article/details/78806448?spm=1001.2014.3001.5502*/

#include <stdio.h>
#include<iostream>
#include <math.h>
#include <string.h>
#include <math.h>

using namespace std;

#define XYZ_F_J "D:\j.txt"
#define DESIGN_DT "D:\dh.txt"


#define RAD2ANG (3.1415926535898/180.0)
#define ANG2RAD (180.0/3.1415926535898)
#define IS_ZERO(var) if(abs(var) < 1e-6 ){var = 0;} 

#define MATRIX_N 4


typedef struct {
    double joint_v;  //joint variable
    double length;
    double d;
    double angle;
}param_t;


double matrix_A1[MATRIX_N][MATRIX_N];
double matrix_A2[MATRIX_N][MATRIX_N];
double matrix_A3[MATRIX_N][MATRIX_N];
double matrix_A4[MATRIX_N][MATRIX_N];
double matrix_A5[MATRIX_N][MATRIX_N];
double matrix_A6[MATRIX_N][MATRIX_N];

double matrix_toolxyz[MATRIX_N][MATRIX_N];


void initmatrix_A(param_t* p_table);
void calculate_matrix_A(double matrix[MATRIX_N][MATRIX_N], param_t* p_param);

void matrix_mul(double matrix_a[MATRIX_N][MATRIX_N],
    double matrix_b[MATRIX_N][MATRIX_N],
    double matrix_result[MATRIX_N][MATRIX_N]);

void matrix_add(double matrix_a[MATRIX_N][MATRIX_N],
    double matrix_b[MATRIX_N][MATRIX_N],
    double matrix_sum[MATRIX_N][MATRIX_N], int m, int n);

void matrix_copy(double matrix_a[MATRIX_N][MATRIX_N],
    double matrix_b[MATRIX_N][MATRIX_N], int m, int n);

void initmatrix_tool(double toolx, double tooly, double toolz);

void printmatrix(double matrix[MATRIX_N][MATRIX_N], int m, int n)
{
    int i, j;

    for (i = 0; i < m; i++) {
        for (j = 0; j < n; j++) {
            printf(" %lf ", matrix[i][j]);
        }
        printf("n");
    }
    printf("n");

}

void printmatrix_1(double matrix[MATRIX_N][1], int m, int n)
{
    int i, j;

    for (i = 0; i < m; i++) {
        for (j = 0; j < n; j++) {
            printf(" %lf ", matrix[i][j]);
        }
        printf("n");
    }
    printf("n");

}


int main()
{

    double matrix_T1[MATRIX_N][MATRIX_N];
    double matrix_T2[MATRIX_N][MATRIX_N];
    double matrix_T3[MATRIX_N][MATRIX_N];
    double matrix_T4[MATRIX_N][MATRIX_N];
    double matrix_T5[MATRIX_N][MATRIX_N];
    double matrix_T6[MATRIX_N][MATRIX_N];

    double toolx = 0, tooly = 0, toolz = 0, toolrx = 0, toolry = 0, toolrz = 0;
    double worldx = 0, worldy = 0, worldz = 0, worldrx = 0, worldry = 0, worldrz = 0;

    param_t param_table[6] = { 0 };
    memset(param_table, 0, sizeof(param_table));

    FILE* fp = NULL;

    fp = fopen(XYZ_F_J, "r");
    if (fp == NULL) {
        perror("open J1_J6 file errorn");
        return 0;
    }
    fscanf(fp, "%lf%lf%lf%lf%lf%lf",
        &param_table[0].joint_v,
        &param_table[1].joint_v,
        &param_table[2].joint_v,
        &param_table[3].joint_v,
        &param_table[4].joint_v,
        &param_table[5].joint_v
    );
    printf("j1...j6n%lf %lf %lf %lf %lf %lfn",
        param_table[0].joint_v,
        param_table[1].joint_v,
        param_table[2].joint_v,
        param_table[3].joint_v,
        param_table[4].joint_v,
        param_table[5].joint_v
    );


    //将机器人关节角度转换成弧度
    param_table[0].joint_v *= RAD2ANG;
    param_table[1].joint_v *= RAD2ANG;
    param_table[2].joint_v *= RAD2ANG;
    param_table[3].joint_v *= RAD2ANG;
    param_table[4].joint_v *= RAD2ANG;
    param_table[5].joint_v *= RAD2ANG;

    fclose(fp);

    fp = fopen(DESIGN_DT, "r");
    if (fp == NULL) {
        perror("open param_table file errorn");
        return 0;
    }

    //读入关节参数
    int i;
    for (i = 0; i < 6; i++) {
        fscanf(fp, "%lf%lf%lf",
            &param_table[i].length,
            &param_table[i].d,
            &param_table[i].angle);
    }
    fclose(fp);

    param_table[0].angle *= RAD2ANG;
    param_table[1].angle *= RAD2ANG;
    param_table[2].angle *= RAD2ANG;
    param_table[3].angle *= RAD2ANG;
    param_table[4].angle *= RAD2ANG;
    param_table[5].angle *= RAD2ANG;

    initmatrix_A(param_table);

    计算变换矩阵 matrix T1---T6
    matrix_copy(matrix_A1, matrix_T1, MATRIX_N, MATRIX_N);

    matrix_mul(matrix_T1, matrix_A2, matrix_T2);

    matrix_mul(matrix_T2, matrix_A3, matrix_T3);

    matrix_mul(matrix_T3, matrix_A4, matrix_T4);

    matrix_mul(matrix_T4, matrix_A5, matrix_T5);

    matrix_mul(matrix_T5, matrix_A6, matrix_T6);


    float sy = sqrt(matrix_T6[0][0] * matrix_T6[0][0] + matrix_T6[0][1] * matrix_T6[0][1]);
    bool singular = sy < 1e-6; // If

    float rx, ry, rz;
    if (!singular)
    {
        rx = atan2(-matrix_T6[1][2], matrix_T6[2][2]) * ANG2RAD;
        ry = atan2(matrix_T6[0][2], sy) * ANG2RAD;
        rz = atan2(-matrix_T6[0][1], matrix_T6[0][0]) * ANG2RAD;
    }
    else
    {
        rx = atan2(matrix_T6[2][1], matrix_T6[1][1]) * ANG2RAD;
        ry = atan2(matrix_T6[0][2], sy) * ANG2RAD;
        rz = 0;
    }
    IS_ZERO(rx);
    IS_ZERO(ry);
    IS_ZERO(rz);

    printf("n----curent x, y, z, rx, ry,rz-----n%lf n %lfn %lfn %lf n %lfn %lfn ",
        matrix_T6[0][3], matrix_T6[1][3],
        matrix_T6[2][3], rx , ry , rz );


}

void initmatrix_A(param_t* p_table)
{//计算关节坐标矩阵 matrix A1--A6
    calculate_matrix_A(matrix_A1, p_table + 0);

    calculate_matrix_A(matrix_A2, p_table + 1);

    calculate_matrix_A(matrix_A3, p_table + 2);

    calculate_matrix_A(matrix_A4, p_table + 3);

    calculate_matrix_A(matrix_A5, p_table + 4);

    calculate_matrix_A(matrix_A6, p_table + 5);
}

void calculate_matrix_A(double matrix[MATRIX_N][MATRIX_N], param_t* p_param)
{//根据关节参数计算矩阵 
    double* pmatrix = (double*)matrix;
    double value, var_c, var_s, angle_c, angle_s;

    var_c = cos(p_param->joint_v);
    IS_ZERO(var_c);
    var_s = sin(p_param->joint_v);
    IS_ZERO(var_s);
    angle_c = cos(p_param->angle);
    IS_ZERO(angle_c);
    angle_s = sin(p_param->angle);
    IS_ZERO(angle_s);

    *pmatrix++ = var_c;

    *pmatrix++ = -var_s * angle_c;

    *pmatrix++ = var_s * angle_s;

    *pmatrix++ = p_param->length * var_c;

    *pmatrix++ = var_s;

    *pmatrix++ = var_c * angle_c;

    *pmatrix++ = -var_c * angle_s;

    *pmatrix++ = p_param->length * var_s;

    *pmatrix++ = 0;
    *pmatrix++ = angle_s;
    *pmatrix++ = angle_c;
    *pmatrix++ = p_param->d;

    *pmatrix++ = 0;
    *pmatrix++ = 0;
    *pmatrix++ = 0;
    *pmatrix = 1;

}

void initmatrix_tool(double toolx, double tooly, double toolz)
{
    matrix_toolxyz[0][0] = toolx;
    matrix_toolxyz[1][0] = tooly;
    matrix_toolxyz[2][0] = toolz;

   /* 初始化 toolrx, tooly, toolz */

}

void matrix_mul(double matrix_a[MATRIX_N][MATRIX_N],
    double matrix_b[MATRIX_N][MATRIX_N],
    double matrix_result[MATRIX_N][MATRIX_N])
{
    int i, j, k;
    double sum;

    /*嵌套循环计算结果矩阵（m*p）的每个元素*/
    for (i = 0; i < MATRIX_N; i++)
        for (j = 0; j < MATRIX_N; j++)
        {
            /*按照矩阵乘法的规则计算结果矩阵的i*j元素*/
            sum = 0;
            for (k = 0; k < MATRIX_N; k++)
                sum += matrix_a[i][k] * matrix_b[k][j];
            matrix_result[i][j] = sum;
        }
}

void matrix_add(double matrix_a[MATRIX_N][MATRIX_N],
    double matrix_b[MATRIX_N][MATRIX_N],
    double matrix_sum[MATRIX_N][MATRIX_N], int m, int n)
{
    int i, j;

    for (i = 0; i < m; i++) {
        for (j = 0; j < n; j++) {
            matrix_sum[i][j] = matrix_a[i][j] + matrix_b[i][j];
        }
    }

}


void matrix_copy(double matrix_src[MATRIX_N][MATRIX_N],
    double matrix_des[MATRIX_N][MATRIX_N], int m, int n)
{
    int i, j;
    for (i = 0; i < m; i++) {
        for (j = 0; j < n; j++) {
            matrix_des[i][j] = matrix_src[i][j];
        }
    }
}

验证(UR5e)

j . t x t : j.txt: j.txt:

57.357.357.357.357.357.3

输出：

xyzrxryrz
174.032973-75.257828-464.848688-106.15888264.78299767.592110

robodk C#API结果：
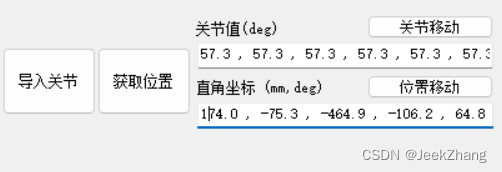
请添加图片描述

xyzrxryrz
174.0-75.3-464.9-106.264.867.6

参考资料：

6轴机器人运动学正解,逆解1
机器人导论 学习笔记2 - 运动学（正解）
欧拉角，四元数，旋转矩阵相互转化（c++, python)

最后

以上就是醉熏小霸王最近收集整理的关于6轴机器人运动学（正解）理论部分的全部内容，更多相关6轴机器人运动学（正解）理论部分内容请搜索靠谱客的其他文章。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(205)

相关文章

6自由度机械臂
6自由度机械臂
机器人可操作度 matlab,并联机器人可操作度分析的蒙特卡罗方法
机器人可操作度 matlab,并联机器人可操作度分析的蒙特卡罗方法
六自由度机器人（机械臂）运动学建模及运动规划系列（一）——简介
六自由度机器人（机械臂）运动学建模及运动规划系列（一）——简介
基于蒙特卡洛方法的机器人工作空间MATLAB仿真
基于蒙特卡洛方法的机器人工作空间MATLAB仿真
6轴机器人运动学（正解）理论部分
6轴机器人运动学（正解）理论部分
六轴机械臂DIY（一）机械臂DIY总体规划
六轴机械臂DIY（一）机械臂DIY总体规划
六自由度机器人（机械臂）运动学建模及运动规划系列（四）——轨迹规划
六自由度机器人（机械臂）运动学建模及运动规划系列（四）——轨迹规划
六自由度机器人（机械臂）运动学建模及运动规划系列（五）——避障路径规划
六自由度机器人（机械臂）运动学建模及运动规划系列（五）——避障路径规划

评论列表共有 0 条评论

立即
投稿
返回
顶部