JC验算点法matlab程序设计

Implement JC algorithm in MATLAB

案例：已知非线性状态方程 567fr-0.5H² =0, f 服从正态分布， =0.6 ，变异系数 =0.131 ， r 服从正态分布， =2.18 ， =0.03 ； H 服从对数正态分布， =32.8, =0.03. 用 JC 法计算可靠指标 及设计验算点坐标（ f* ， r* ， H* ）。

解：功能函数梯度为 g （ f ， r ， H ） = （ 567r ， 567f ， -H ） ^T 。关于如何确定对数正态分布的参数见附录。

Matlab 代码如下：

clear;clc;

muX=[0.6;2.18;32.8]; cvX=[13.1;3;3]/100; sigmaX=cvX.*muX;

sLn=sqrt(log(1+(sigmaX(3)/muX(3))^2));mLn=log(muX(3))-sLn^2/2;

muX1=muX;sigmaX1=sigmaX;

x=muX; normX=eps;

while abs(norm(x)-normX)/normX>1e-6

    normX=norm(x);

    g=567*x(1)*x(2)-x(3)^2/2;

    gX=[567*x(2);567*x(1);-x(3)];

    cdfX=logncdf(x(3),mLn,sLn);

    pdfX=lognpdf(x(3),mLn,sLn);

    nc=norminv(cdfX);

     sigmaX1(3)=normpdf(nc)/pdfX;

    muX1(3)=x(3)-nc*sigmaX1(3);

    gs=gX.*sigmaX1;

    alphaX=-gs/norm(gs);

    bbeta=(g+gX'*(muX1-x))/norm(gs)

    x=muX1+bbeta*sigmaX1.*alphaX

end

结果：设计验算点坐标（ f* ， r* ， H* ） = （ 0.4561 ， 2.1590 ， 33.4178 ），beta =1.9645 。

参考文献：

1 ，张亮，赵娜 . 用 MATLAB 实现 JC 法计算结构可靠度程序 . 电脑知识与技术 . Vol.5,No.29, October 2009 ， pp.8181 — 8182,8185.

2, http://mathworld.wolfram.com/LogNormalDistribution.html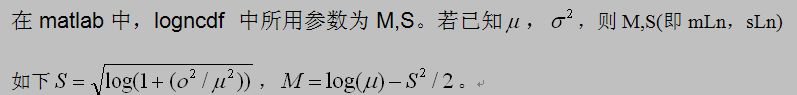

最后

以上就是天真哈密瓜为你收集整理的JC验算点法matlab程序设计的全部内容，希望文章能够帮你解决JC验算点法matlab程序设计所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。