在结构可靠性分析中，代理模型法是很重要的一种方法，包括响应面法、Kriging等，我这两年一直在学这方面的知识，尤其是刚开始的时候，在网上很难找到资料，看论文是最好的方法。这里是我对响应面法的一些理解，及其主要内容。

背景

传统工程设计以安全因子来保证结构的稳定，例如，通常以结构的强度和应力的比值作为安全因子值。但是现实生活中强度和应力这些参数并不是一个常数，是随机的，这就导致传统的安全因子法给出的结果不太可信。
而概率分析方法就是用随机变量对应力、强度等参数进行建模（正态分布，威布尔分布等），然后计算其失效概率。
那么怎么定义失效呢。比如说：对于一个桁架结构，在外力的影响下，我们怎么判定他在什么情况下是失效的呢？这是工程师的前期工作，比如假设某一关键节点的位移大于某一值，我们就判定该结构是失效的。这并不是响应面法的重点，便不做介绍了。
假设我们已知失效的标准了，那么我们假设，随机扰动因素为向量X，记结构响应为Y，则Y与X之间可用一隐式函数关联，即
$$Y=G(X)$$

我们假设Y<0为失效，Y>0为正常，那么Y=0就是一个临界状态，也称极限状态。而概率分析的主要目的是，找到结构的失效概率，即
$$P(Y<0)=P(G(X))<0$$

这么看来，$G(X)=0$就是一个分界，而且相当重要了。所谓代理模型法就是找到这个分界，并用简单的显式函数进行替代。
那么为什么不直接对结构进行操作，而要用代理模型呢，因为当结构胶复杂时，我们很难得到结构的响应Y与随机扰动X的显式表达式，那么我们就要用到ANSYS等有限元软件计算，而这些软件的计算是很耗时的，而且我们用Monte Carlo仿真时一般要用10⁵~10⁷次左右，这极大地增加了我们的计算负担。因此，我们要用代理模型表达结构的响应，即用代理模型的结果来替代ANSYS计算的结果。而且我们只关心响应值$G(X)$是否小于0，对其真实响应值是1还是1000并不关心，因此G(X)=0的临界就十分关键。所以代理模型的关键就是对隐式函数$G(X)=0$的显式精确表达。这一点在Kriging算法中体现的尤为明显。
一般代理模型的主要步骤是，选取试验点，用ANSYS计算试验点的响应值，用函数进行拟合，判断是否拟合结果准确，不准确继续选点，拟合，直到达到某一设定的精度为止。

代理模型的基本思想

代理模型就是用简单的函数来近似替代复杂耗时的计算（有限元计算等）。而结构可靠性分析中，将结构分为两种状态：安全和失效。因此只需要区分结构响应G(X)的状态即可，并不需要对其真实的响应值精度有过多要求。因此代理模型只要准确地区分出其状态即可，这就是为什么代理模型只关注于临界状态部分。把极限状态曲面拟合好了，就可以区分出其状态了。
而代理模型的评价指标有两个，精度和效率，由于显式函数的计算是很快的，而结构响应的计算时间是很久的，所以效率的体现就是用结构响应计算的调用次数来表征。因此要用尽量少的试验点获得尽量精确的拟合。

响应面法的几个主要组成部分

响应面法主要包括：

1. 试验点的选取
2. 函数形式的选取
3. 迭代控制方式
4. 收敛准则

下面将详细介绍上述几个方面。

试验点的选取

为了更好地拟合$G(X)=0$这一曲面，我们必然要选取合适的试验点，然后进行拟合。这就涉及到试验设计方面，常见的几种实验设计包括，拉丁超立方，均匀设计，正交设计，星形设计法等。经典响应面采用的是Bucher提出的星形设计法。其基本思想就是，围绕抽样中心，沿各随机变量所在坐标轴正负方向偏离中心点一定距离选取试验点。如下图所示

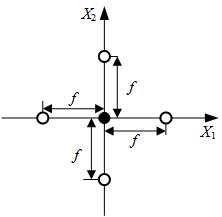
该试验设计是在标准正态空间中，即所有变量都是标准正态变量，因此在进行实验设计时要将所有变量进行当量正态化，当量正态化方法有很多，我常用的是JC法。图中的$f$表示偏移距离，一般取值为1~3，黑圈表示抽样中心点，白圈表示抽取的试验点，每次抽取的试验点都包括抽样中心点。

函数形式的选取

常用响应面法的函数形式是Bucher和Bourgund提出的不含交叉项的二次多项式。由此可知，函数中有2n+1个待定系数，而Bucher提出的星形设计法每次选取也是2n+1个试验点，因此完美契合（毕竟都是自己的方法嘛，当然要契合了）。
为什么说完美契合呢，因为刚开始，响应面法的每次迭代时，用来确定拟合函数的系数用的都是本次迭代选取的试验点，前面的试验点是不用的。所以正好可以解出2n+1个系数。由于之前的试验点不用，所以会损失很多信息，之后的学者便将前面选取的试验点也加入到了本次迭代的拟合中。
这有好有坏，好处在于，可以更快的收敛；坏处在于，由于前面选取的试验点距离极限状态G(X)=0较远，但是在拟合时用的是最小二乘拟合，这就导致拟合效果（精度）较差。
既然有坏处，那么怎么修改呢？
于是研究学者发明了权重的方法来改善这种缺陷。Kaymaz和Mcmahon于2005年率先提出了加权响应面法的概念，他们采用指数加权法结合符号判断方法构建响应面模型，分别对高度非线性和单点畸变算例进行验证，结果表明该法相较于传统的最小二乘法构建的常规响应面在精度上有所提高¹。Nguyen和Sellier等在2009年提出了“双加权响应面法”²。

权重的基本思想

由上面可知，不同试验点在拟合极限状态曲面的时候发挥的作用是不同的，而最小二乘拟合的过程中，将所有试验点当做同等对待。给每个试验点加权重就是为了使得更加重要的点发挥的作用越大。加权方式一般有两种，是基于两种思想进行设计的。
第一种比较好理解，基于试验点的响应值G(X)到极限状态曲面的距离。越接近于极限状态曲面，则越重要。原因是，代理模型的基本思想就是对极限状态曲面的拟合，那么越接近于极限状态，该试验点与极限状态曲面的相关性越大。这和随机过程里的相关性类似，两个点越接近其相关性越高。
于是便形成了几种权重函数，因为笔者对markdown插入公式不太熟悉，这里就不一一列举了，需要的请自行查找文献。
第二种加权方式就比较难理解一点，当然只是相对于前一种，其实也是很简单的。我们知道响应面法一般是在标准正态空间这么一个概率空间中进行操作的，那么即使同样是在极限状态曲面附近，不同区域的概率密度也是不同的。对于概率密度较低的区域，即使对极限状态曲面的拟合精度较低，对于最后失效概率的计算的影响也是很小的。反之，概率密度较高的区域，其拟合效果对最终的概率计算影响是很大。故而为了进一步提高算法的效率，研究人员就发明了第二种加权方式。
在提到第二种加权方式时，就不得不提到最大失效点（Most Probable Point，MPP，其实还有其他叫法，真实失效点、可靠性设计点等）这一概念。顾名思义，就是最有可能失效的点，也就是说，在所有失效点中，它最有可能发生（概率密度最大的点），详细解释可以参考杜小平老师编写的这章内容³。

总之就是，MPP附近的区域是最重要的，最有可能失效的，概率密度最大的。那么，研究人员就将试验点到MPP的欧拉距离作为一个参考，距离越小越重要，距离越大重要性就低。因此也就有了第二种权重方式。
如果想获取具体权重函数，可以参考Goswami和Ghosh写的这篇论文⁴。

总之一句话，给试验点赋权就是用不同的圈体现试验点在响应面拟合中的不同作用效果，我们也可以根据自己的经验来自己定义权重函数。
当然，权重函数也有缺陷，有可能陷入病态，当然也有人在这方面做了一些工作，感兴趣的可以阅读这篇论文⁵。

双加权的方式还有一点需要讨论，两个权重之间的关系，Nguyen和Sellier等²用的是两者相乘，其实也可以相加，而且相加的话还可以确定两个权重的作用大小。

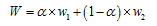
迭代控制方式

之前介绍，迭代过程是，选点，拟合，判断收敛，继续选点，拟合……。这里就有一个问题，后续迭代选点应该怎么选。上面介绍了根据抽样中心点来选点，抽样中心点的确定就是关键。下面就是传统响应面法的迭代方式：

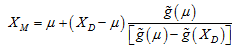
其中，X_M为抽样中心点，X_D是上一次迭代的设计验算点（MPP），$\mu$表示变量的均值点。$g(\mu )$表示该点的响应值。

收敛准则

Bucher和Bourgund认为迭代两次即可得到满意的可靠度指标近似值，但Rajashekhar和Ellinwood对一些算例使用两次迭代方法求解发现其对某些问题表现不佳，因此Rajashekhar和Ellinwood提出了设置收敛条件进行多次迭代的改进算法。收敛条件主要有三种：可靠性指标，设计点步长，设计点处的导数。原则是每次的变化小于一个设定值时，就判定为收敛。

响应面方法的缺陷及可能改进的地方

缺陷

1. 模型选用的是不含交叉项的二次多项式，对于一些复杂问题的拟合较差，这一点Kriging方法就做的很好；
2. 对比于Kriging方法给出某个点的期望和方差，响应面法给出的是一个定值；
3. 对于高维变量，效率低下，当然这也是所有代理模型的缺点。

改进

2018年发表了一篇关于响应面法的论文⁶，令我受益良多，以下主要根据这篇文章来介绍可以改进的方面。

传统响应面的基本流程图为：

而Hugo的这篇文章提出了一个更为全面的框架：

其创新点在于：

1. 在使用变量之前加上了变量筛选这一条，这在实际工程中是必须的；
2. 对试验设计的区域进行了探索和定义，传统的响应面是在整个空间中进行试验设计，而这片论文却根据结构的灵敏度将实验空间进行了分割，减少了低效率的探索，将试验设计集中到了更有可能发生的地方；
3. 对模型进行选择和验证，传统响应面使用的是固定的模型，具有较强的普适性，但是对于某一特定情况下，效果不一定好，是要对模型进行了选择和验证，增强了模型的灵活性，具体情况具体分析。
4. 在后续迭代的抽样方案上也选择了序贯抽样法，这点的原因我还不太明白。

最后

以上就是温暖白云为你收集整理的结构可靠性分析中响应面方法的基本思想背景代理模型的基本思想响应面法的几个主要组成部分响应面方法的缺陷及可能改进的地方的全部内容，希望文章能够帮你解决结构可靠性分析中响应面方法的基本思想背景代理模型的基本思想响应面法的几个主要组成部分响应面方法的缺陷及可能改进的地方所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。