code用了一定的篇幅写编码以及进制的内容(毕竟书名就叫code),这部分内容我可能兴趣缺缺吧,所以第一篇学习笔记便从加法器写起啦。
目录
-
- 目录
- 用继电器构造简单的逻辑门
- 一个继电器:
- 反向器(非)
- 与门和与非门
- 或门
- 异或
- 二进制半加器
- 二进制全加器
- 多位二进制数加法器
- 工业成品类比
- 多说几句
用继电器构造简单的逻辑门
相对于抽象的与或非,或者现在电路中的精巧原件,作者用线圈与电磁体构造的门形象的描述了一系列的门。作为学习笔记,应以简而明了为要,所以以下省略了作者的大量篇幅,或许会显得不够详细。
一个继电器:
一个电磁铁是两个电路有了关联,开关闭合,灯泡亮。
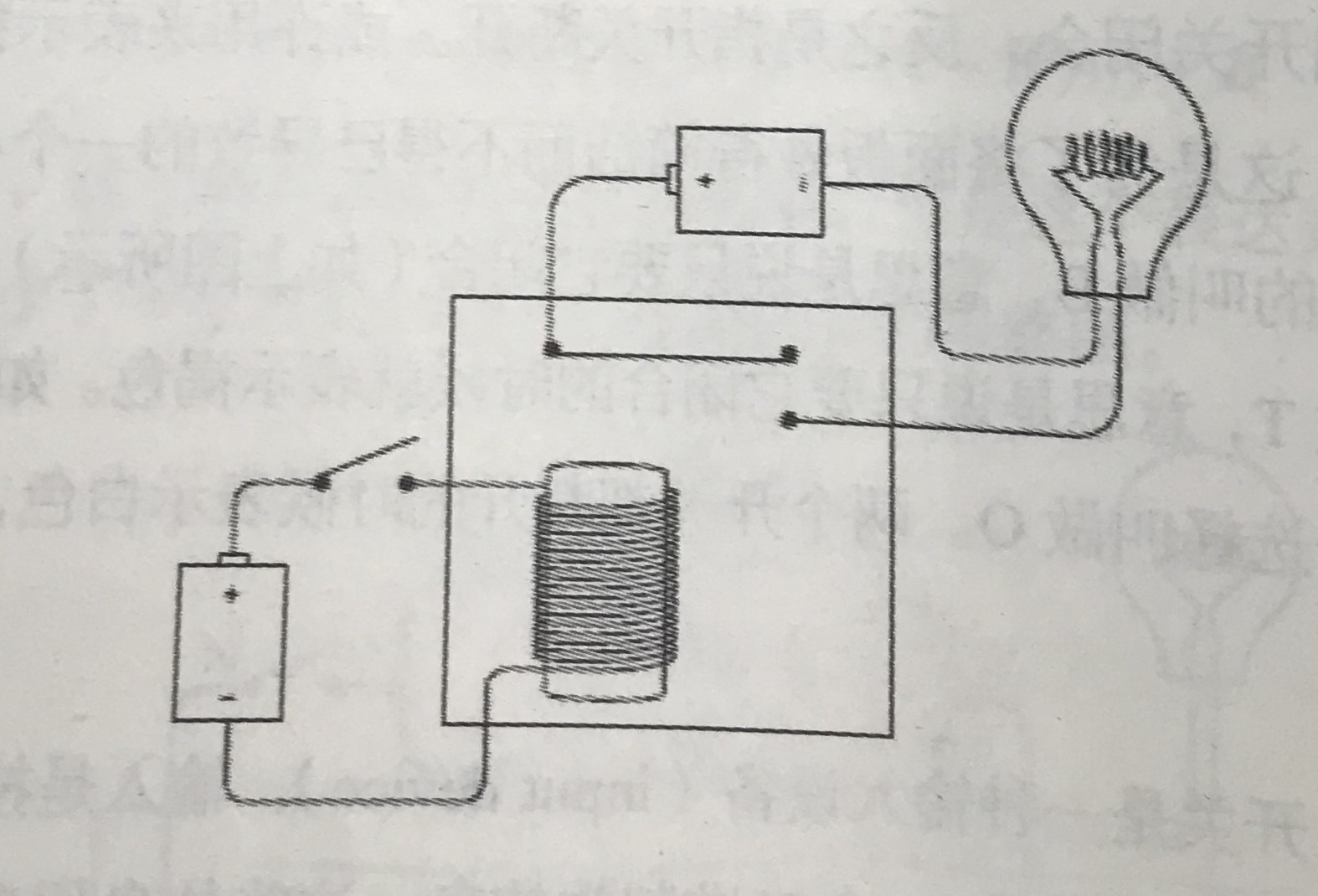
反向器(非)
与继电器极为相像,只不过开关闭合,灯泡灭。
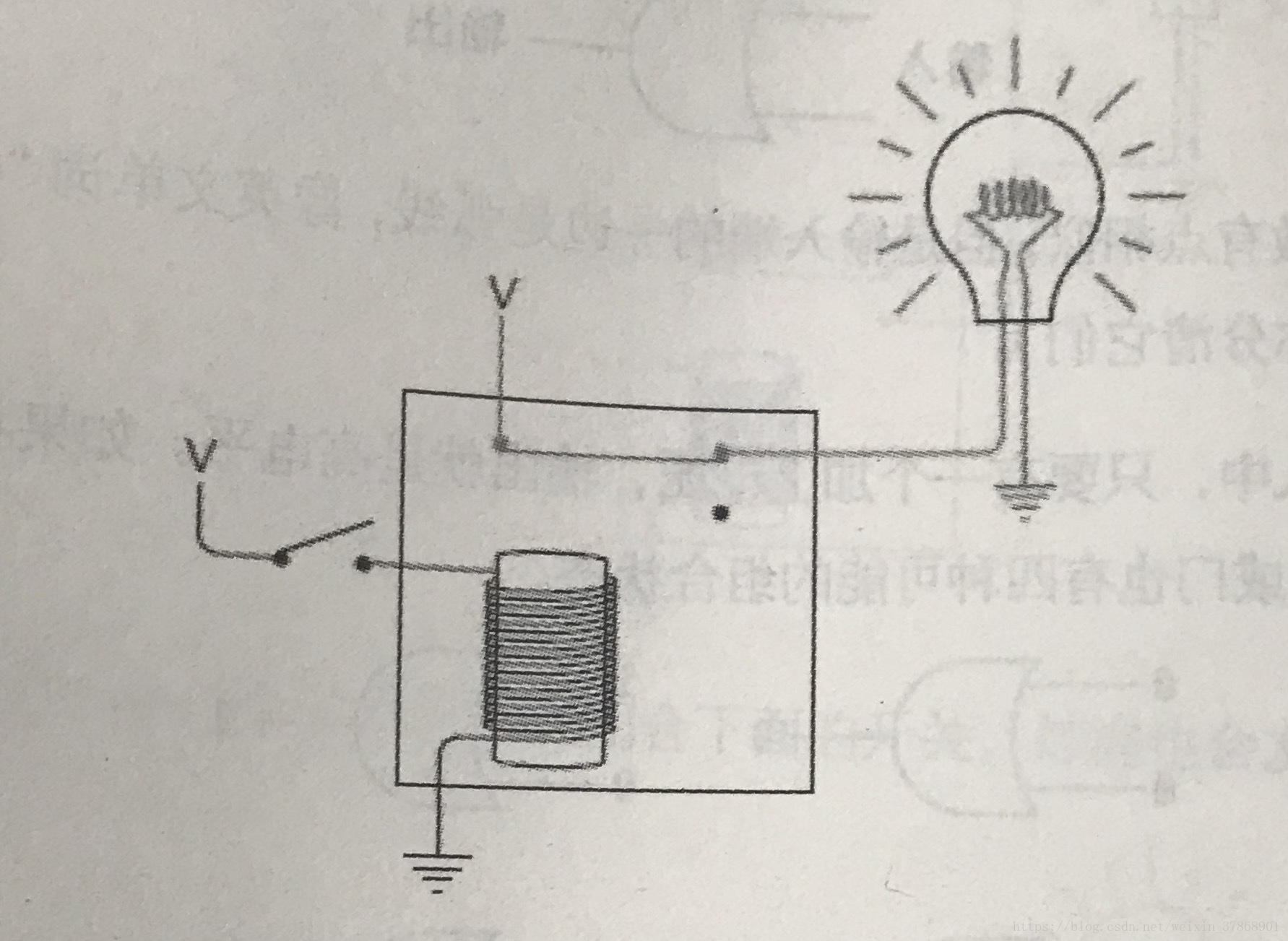
与门和与非门
两个继电器右端电路的串联,当且仅当两个开关闭合,灯泡才亮。
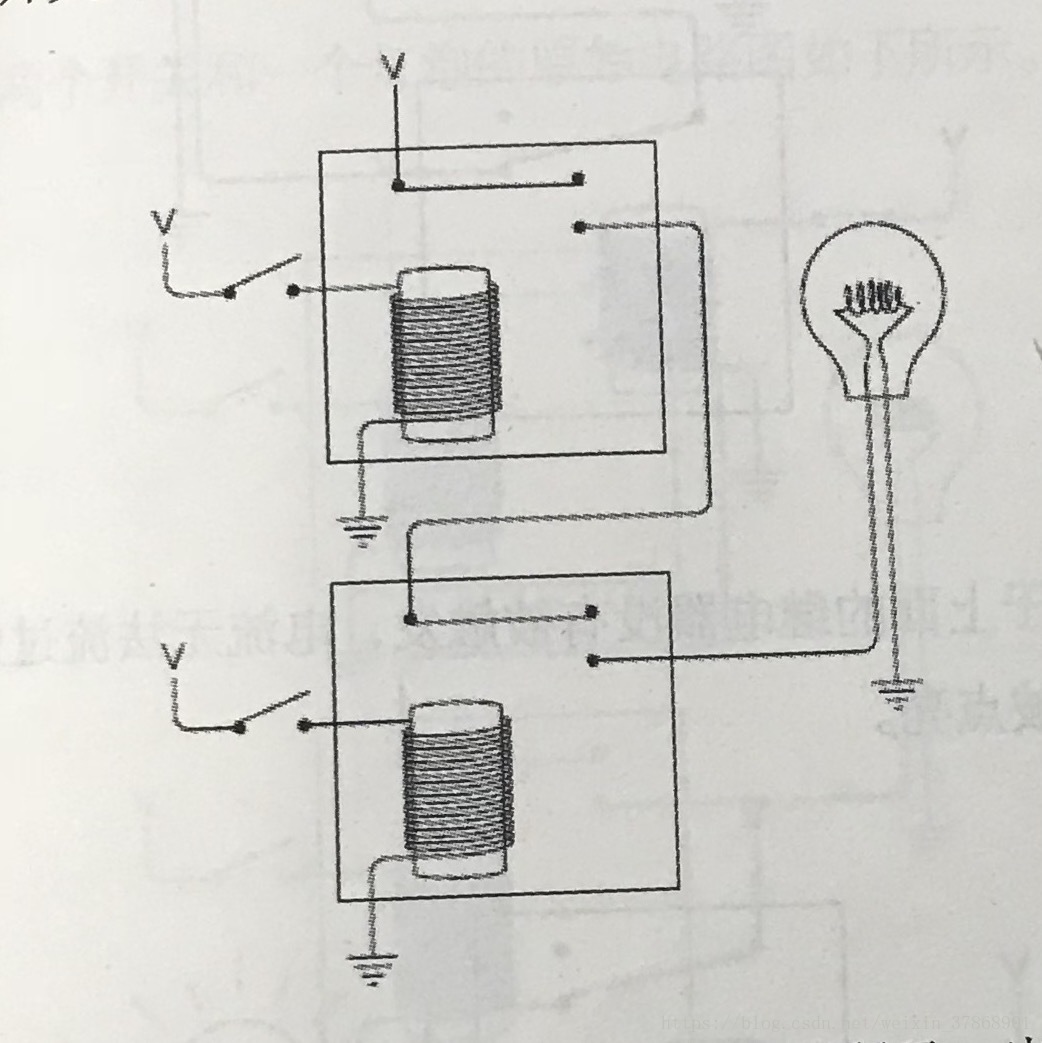
抽象为与门如下
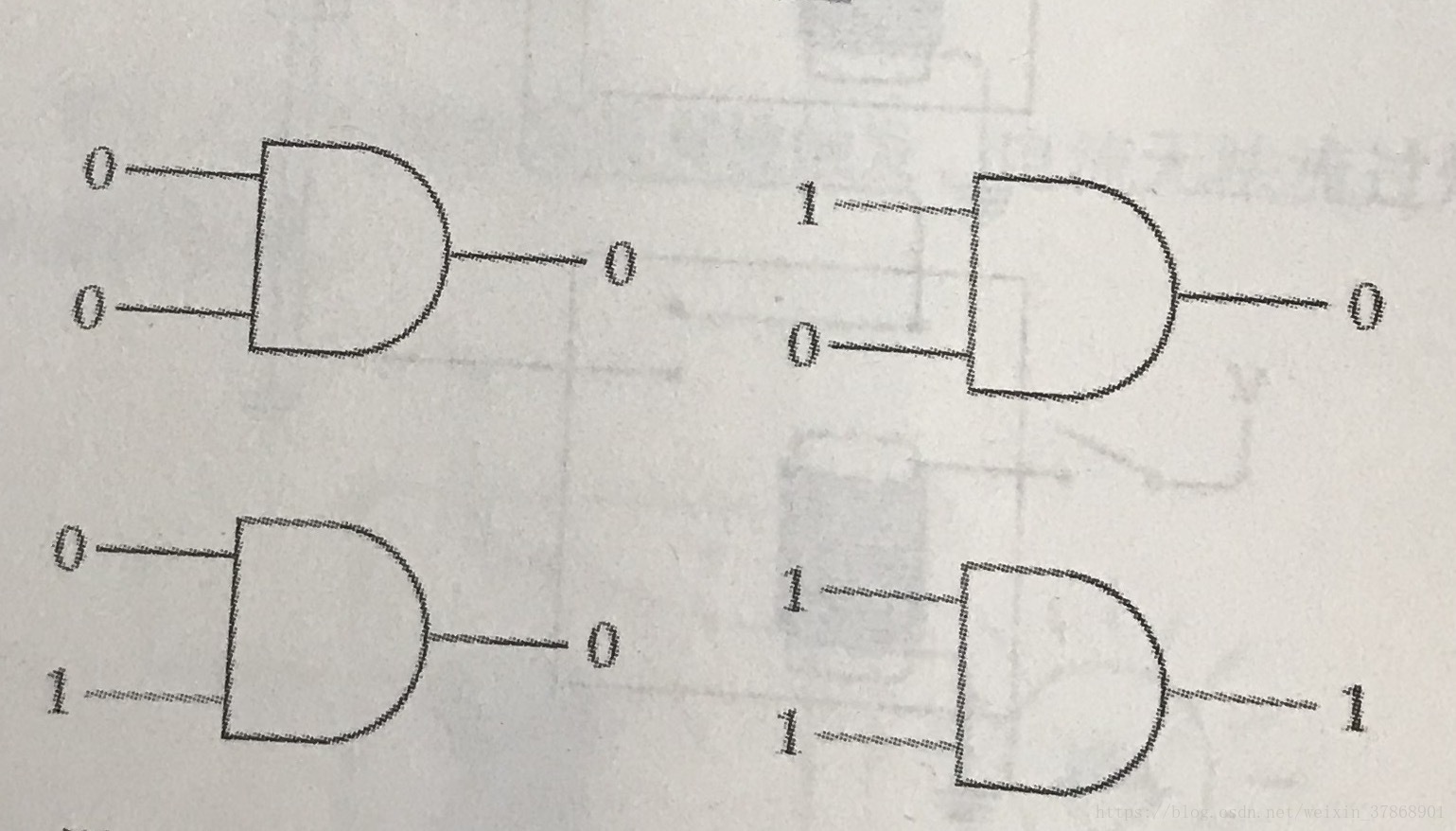
信号1代表开关闭合(高电平输入),信号0代表开关断开(低电平输入),与门列表:
| AND | 0 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
在与门的末尾(即灯泡与输出之间)加一个反向器,得到与非门NAND
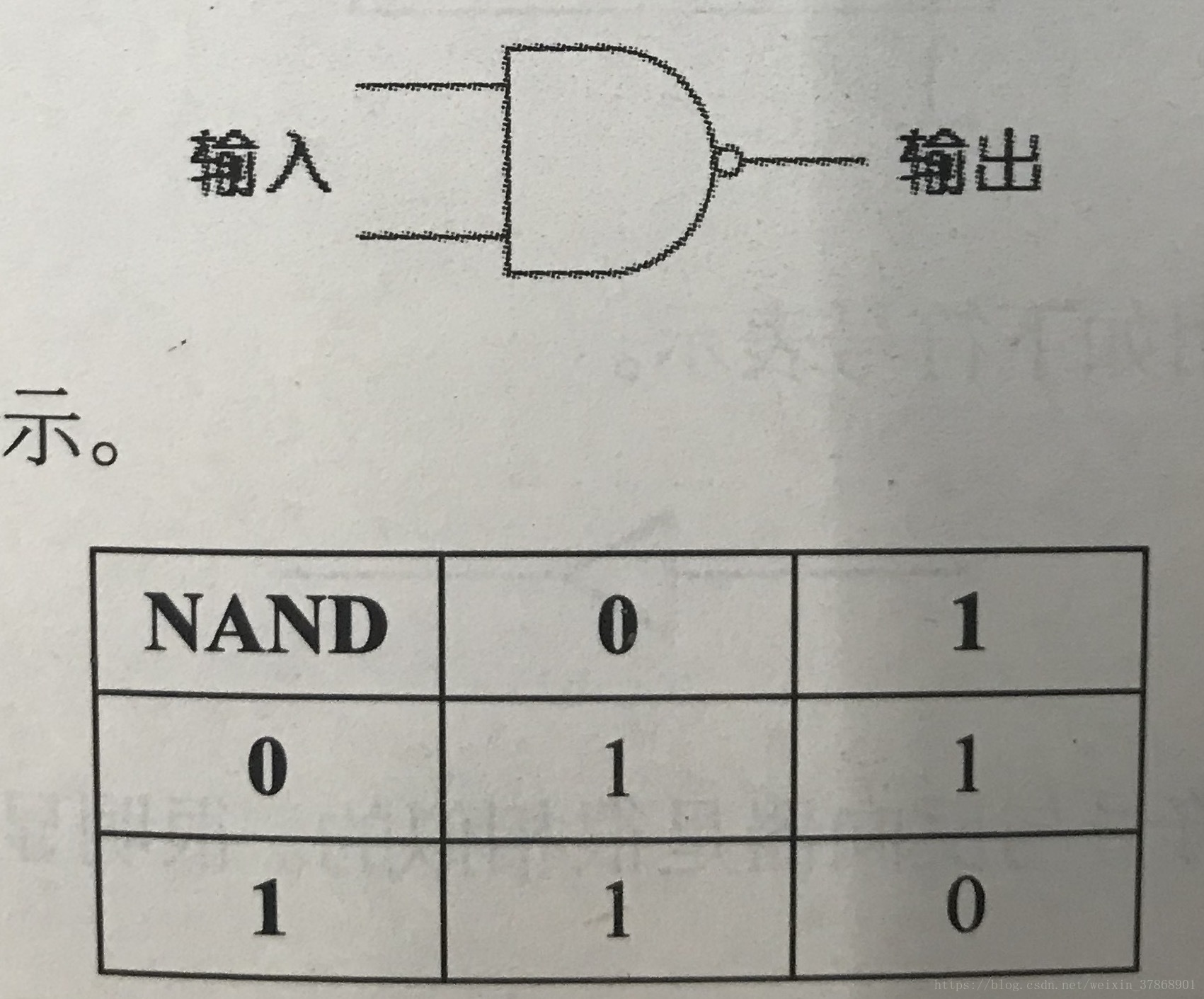
或门
如果说与门是两个继电器的“串联”,那么或门则是“并联”
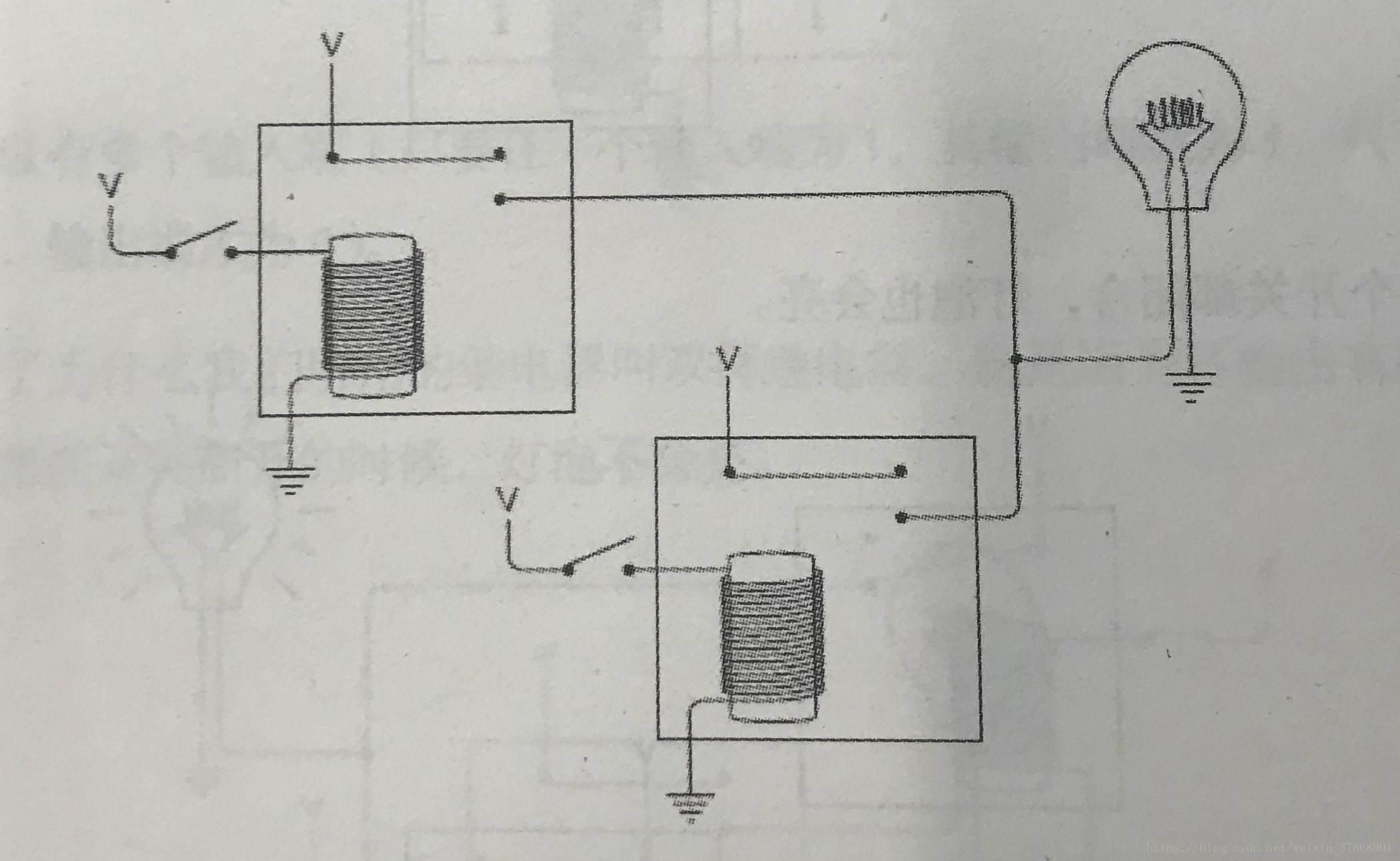
或门符号
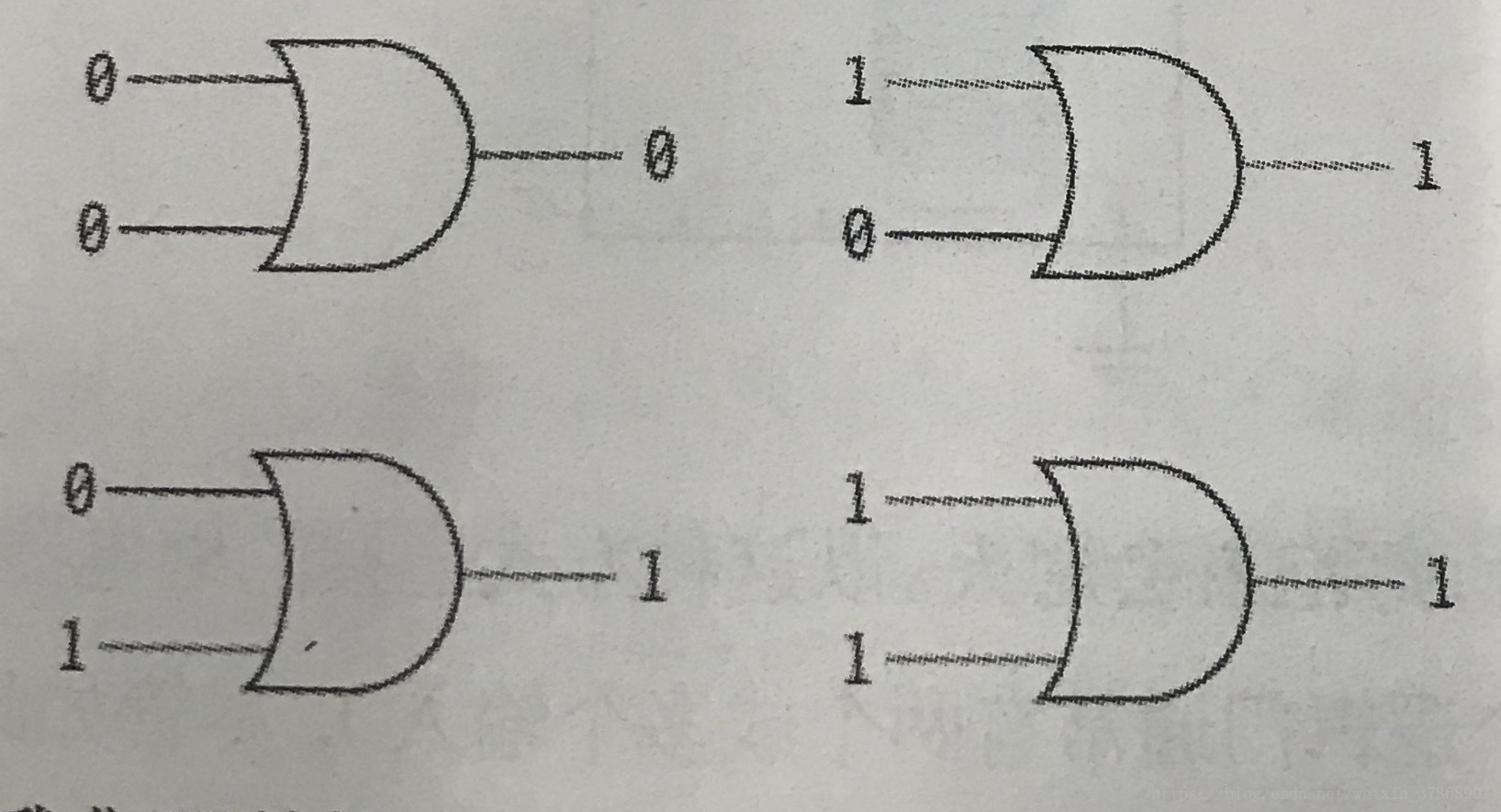
或门列表
| OR | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 1 |
在或门的末尾(即灯泡与输出之间)加一个反向器,得到或非门NOR
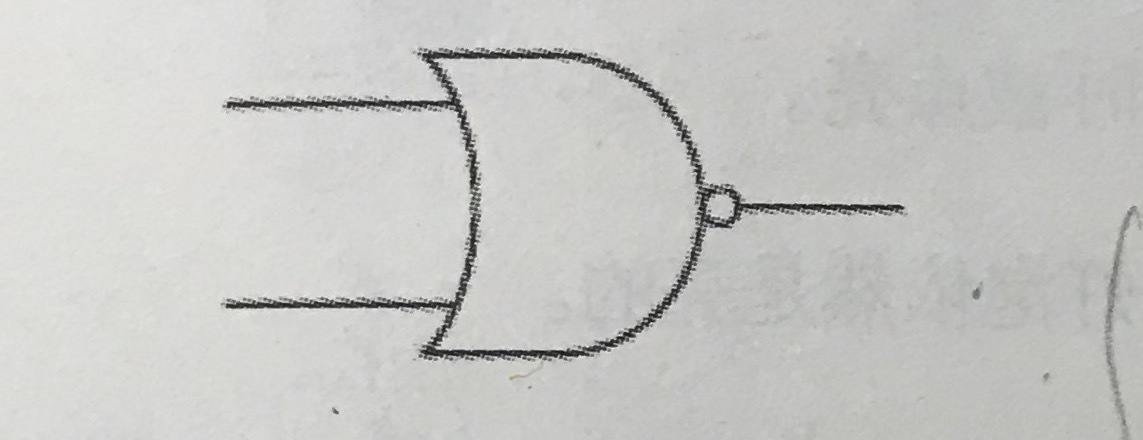
异或
在数理逻辑里,与、非或者或、非就是一个联结词的完备集了,通过其中任意一组既可以表示出所有的联结词。有了与或非,异或门将直接由它们组成。
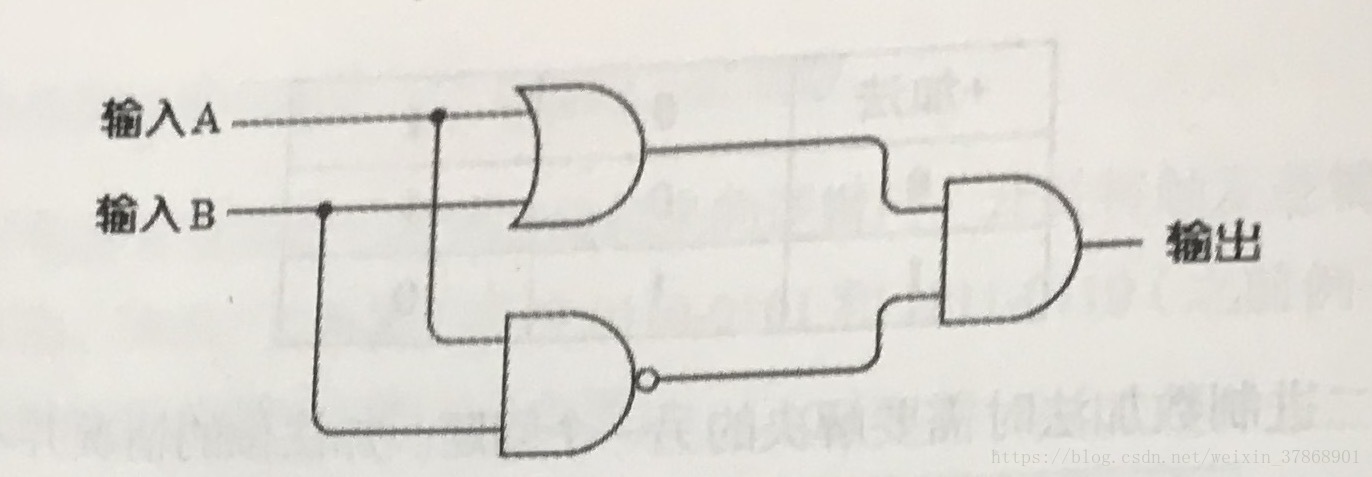
异或门
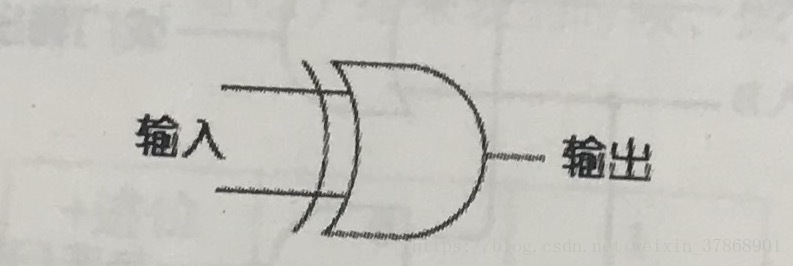
| XOR | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
二进制半加器
由于神奇的二进制“阳阳易数”,通过以上几个门来实现二进制的非进位加法就可行了。
先列出加和表
| + | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
妥妥的一个异或门。
再来个进位表
| 进位 | 0 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
就是一个与门。
那么一位数的二进制半加器就大功告成啦!
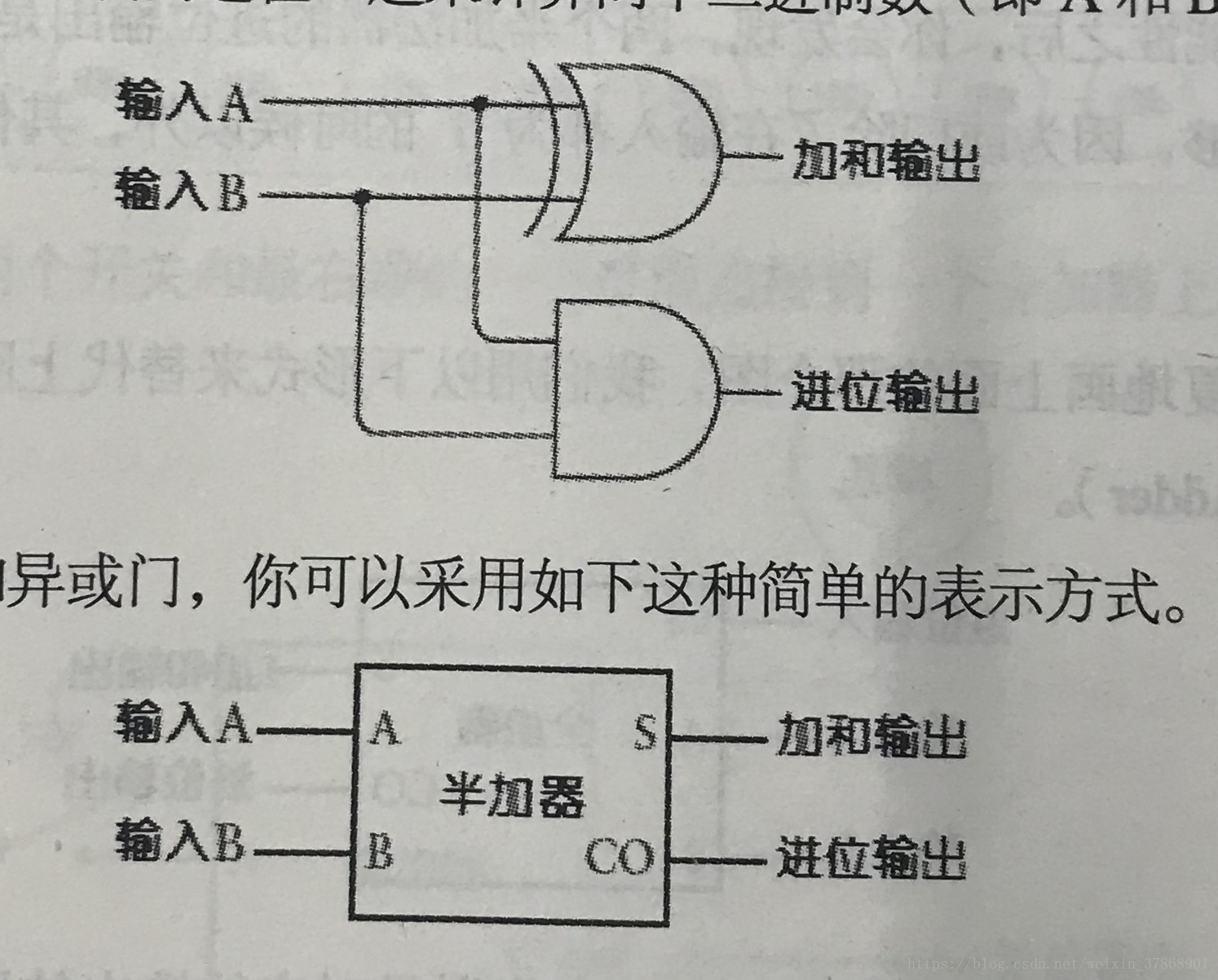
(学到此处如果你和我一样迫不及待的想动手实践,那么你可以考虑考虑通过mc的红石电路来实现它们)
二进制全加器
加法如果在最低位自然不需要考虑进位,但是如果你想搭建一个多位数的加法器,那么输入端也就必须要有一个进位输入,这就是全加器。
比较容易想到的一个方法就是做两次加法,进位输入和第一次加法的结果进行再一次的加法,就可以得到一个完整的全加器啦。当然,第一次加法的结果包括了进位输出和加和输出,那么第二次加法自然也要处理好这两个事情。
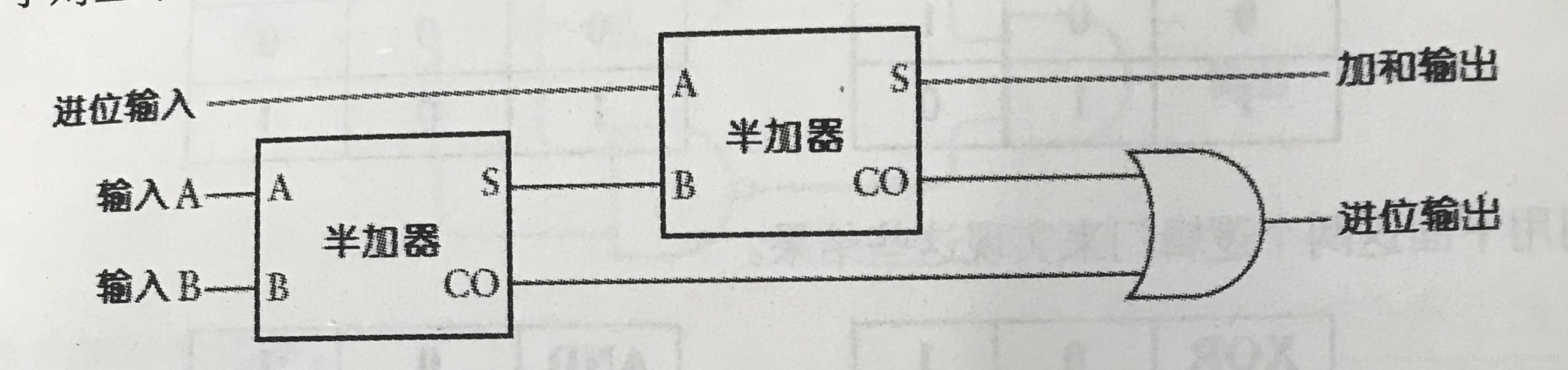
这就组成了一个一位全加器,封装后如下:
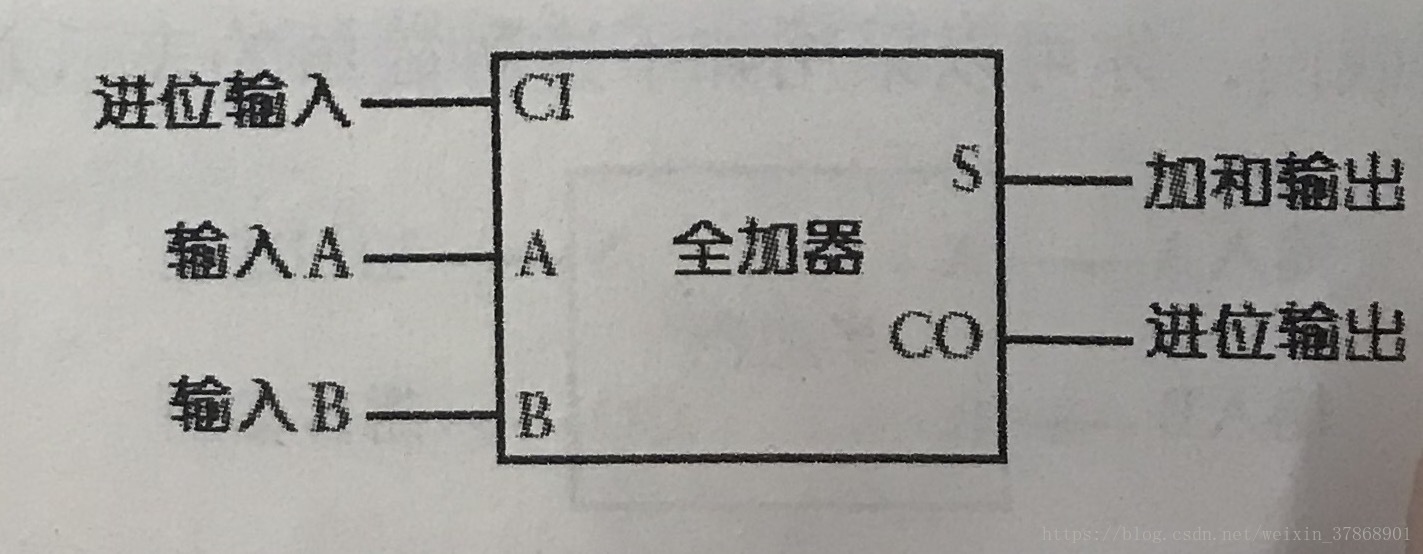
多位二进制数加法器
有了二进制全加器,解决了进位问题,那么要构建多位数的加法器也就水到渠成了。
将全加器倒过来,每个全加器的进位输出连着下一位的进位输入,如此“并联”,既可以得到多位数的加法器了,下图构建的是一个八位加法器。

封装后如下
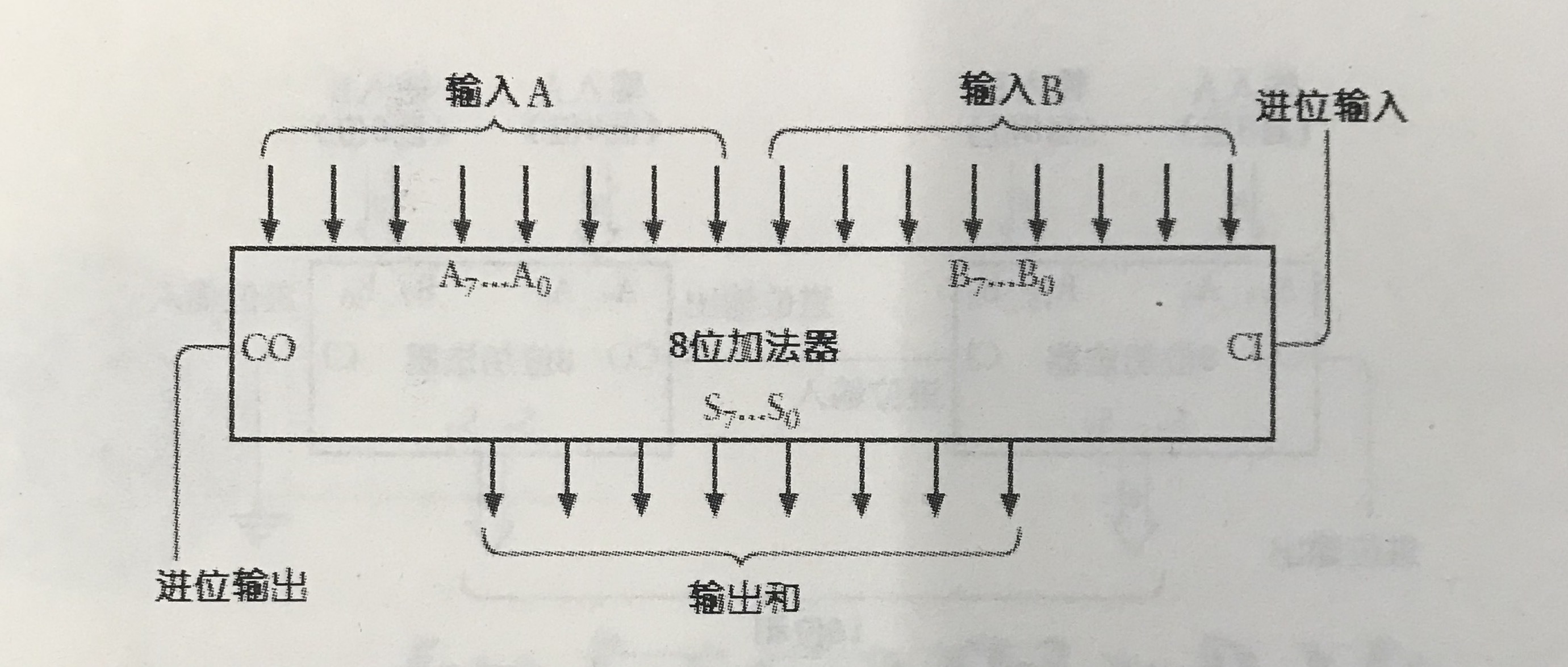
工业成品类比
(没有百度到行波进位加法器,凑合着看吧,大概就是这样的接口了/百度的图/)

多说几句
以上是由比较原始继电器构成的加法器,由于是行波进位,显然效率较低(后一位的加法必须要前一位的结果),书中还提到了一种前置进位电路的加法器,额,俺不会,看了头大,有时间再去了解吧。。。
另外如果没有晶体管,半导体,集成电路的出现,最后的一张图片显然是没有的,构建上述加法器仅仅是为了明白原理,至少面对着最后一个小部件的时候,不会一脸懵逼,知道原理并会使用总是比只知使用不知原理好的。。。
最后
以上就是甜甜墨镜最近收集整理的关于CODE学习笔记一——构建二进制加法器的全部内容,更多相关CODE学习笔记一——构建二进制加法器内容请搜索靠谱客的其他文章。








发表评论 取消回复