【论文导读】（AAAI）Achieving Counterfactual Fairness for Causal Bandit【摘要】【Introduction】实现强盗行为中的反事实公平性通过软干预建立手臂选择模型 D-UCB算法反事实的公平 F-UCB算法结论

54 阅读 0 评论 36 点赞

我是靠谱客的博主幸福芒果，最近开发中收集的这篇文章主要介绍【论文导读】（AAAI）Achieving Counterfactual Fairness for Causal Bandit【摘要】【Introduction】实现强盗行为中的反事实公平性通过软干预建立手臂选择模型 D-UCB算法反事实的公平 F-UCB算法结论，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

因果强化学习！

【注意bandit algorithms的前置知识，理解“手臂”arm、“强盗”bandit】

【摘要】

在在线推荐中，顾客从一个基本分布以顺序和随机的方式到达，在线决策模型根据一定的策略为每个到达的个体推荐一个选定的商品。我们研究如何在每个步骤推荐一个物品，以最大化预期奖励，同时实现用户端的公平，即，共享相似档案的客户将获得类似的奖励，无论他们的敏感属性和被推荐的物品。我们首先提出了基于d-分离的UCB算法(D-UCB)，通过将因果推理纳入强盗模型，并采用软干预对手臂选择策略进行建模，以探索d-分离集在减少探索所需数量方面的利用，以实现较低的累计遗憾。在此基础上，我们提出公平因果强盗(F-UCB)来实现反事实个体的公平。理论分析和实证评价都证明了算法的有效性。

【Introduction】

机器学习中的公平性是最近快速增长的研究课题。虽然有很多工作关注个性化推荐中的公平性（Celis等人，2018；Liu等人，2017；Zhu，Hu和Caverlee，2018），但如何在匪徒推荐中实现个体公平性仍是一项具有挑战性的任务。我们专注于在线推荐，例如，客户被推荐物品，并考虑这样的设置：客户从一个基础分布中以顺序和随机的方式到达，在线决策模型根据一些策略为每个到达的个体推荐一个选择的项目。这里的挑战是如何在每一步选择臂膀，使预期奖励最大化，同时为客户实现用户侧的公平性，也就是说，无论客户的敏感属性和被推荐的项目如何，具有类似特征的客户将获得类似的奖励。

最近研究人员开始在个性化推荐算法的设计中考虑公平性和歧视性（Celis等人，2018；Liu等人，2017；Zhu，Hu和Caverlee，2018；Joseph等人，2016，2018；Jabbari等人，2017；Burke，Sonboli，和OrdonezGauger，2018；Ekstrand等人，2018）。其中，Joseph等人（2016）是第一篇研究经典和情境匪徒中公平性的论文。它定义了单步奖励的公平性，并引入了功利主义公平性的概念，即算法不应该把更高的选择概率放在资格较差的手臂上（例如求职者），而不是放在资格较高的手臂上。沿着这个方向的工作包括（Joseph等人，2018）针对无限和上下文匪徒，（Jabbari等人，2017）针对强化学习，（Liu等人，2017）针对简单随机匪徒设置的基于校准的公平性。然而，所有现有的工作都需要在学习过程的每一轮对武器进行一些公平性约束，这与我们的用户侧公平性设置不同。最近的一项工作（Huang等人，2020）专注于在bandit设置中实现用户侧的公平性，但它只是以启发式的方式来实现基于相关的组级公平性，并没有将因果推理和反事实公平性纳入bandit。

通过将因果推理纳入bandit，我们首先提出了基于d-separation的置信度上限bandit算法（D-UCB），在此基础上我们又提出了公平因果bandit（F-UCB），以实现反事实的个体公平。我们的工作受到最近关于因果强盗的研究的启发（Lattimore, Lattimore, and Reid 2016; Sen等人2017; Lee and Bareinboim 2018, 2019; Lu等人2020），研究如何通过将干预和结果之间的关系表示为因果图以及相关的条件分布来顺序学习最佳干预措施。例如，Lu等人（2020）开发了因果UCB（C-UCB），利用奖励和其直接父母之间的因果关系。然而，与以前的工作不同，我们的算法采用软干预（Correa和Bareinboim 2020）【

在本文中，我们提供了一个数学解决方案来解决这个十年前的辩论。回到我们的例子，为了具体化，政策制定者考虑对未成年人吸烟进行更严格的监管，并对香烟销售征收更高的税。在这种情况下，一个合理的问题可以是--将21岁以下的人的吸烟率抑制在90%的政策会产生什么效果？这样的干预当然是非原子性的（这就意味着应该对这个群体实施100%的吸烟减少），在这种情况下，X的基本机制被一个较软的机制所取代；这些干预有时被称为软干预或随机干预。

Correa J, Bareinboim E. A calculus for stochastic interventions: Causal effect identification and surrogate experiments[C]//Proceedings of the AAAI conference on artificial intelligence. 2020, 34(06): 10093-10100.

】来模拟手臂选择策略，并利用从底层因果图中确定的d-分离集，从而大大减少了实现低累积遗憾所需的探索量。我们表明，我们的D-UCB实现了O˜( p |W| - T)的遗憾约束，其中T是迭代次数，W是因果图中d分离手臂/用户特征和奖励R的集合。作为比较，C-UCB实现了O˜( p |P a(R)| - T)，其中P a(R)是R的父变量，是d分离集的琐碎的解决方案。在我们的F-UCB中，我们在每一轮探索中进一步实现反事实的公平性。反事实的公平性要求，如果个体的敏感属性被改变为其对应的属性，那么该个体将获得的预期奖励保持不变。引入的反事实奖励结合了两种干预措施，一种是对手臂选择的软干预，一种是对敏感属性的硬干预。F-UCB通过在每一轮的武器子集中挑选武器来实现在线推荐中的反事实公平性，其中所有的武器都满足反事实公平性约束。我们的理论分析表明，F-UCB实现了O˜( √ |W|T τ-∆π0)的累积遗憾边界，其中τ是公平性阈值，∆π0表示安全策略π0的最大公平性差异，即一个在所有回合中都是公平的策略。

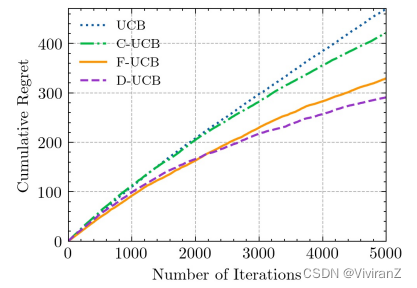
我们在电子邮件运动数据（Lu等人，2020）上进行了实验，其结果显示了使用因果图的dseparation集的好处。我们的D-UCB比两个基线（不利用任何因果信息的经典UCB以及C-UCB）产生的遗憾更少。此外，我们用数字验证了我们的F-UCB保持了良好的性能，同时在每一轮中满足了反事实的个人公平性。相反，基线未能实现公平性，有相当比例的建议违反了公平性约束。我们进一步在成人视频数据集上进行了实验，并将我们的F-UCB与另一个用户端公平强盗算法Fair-LinUCB（Huang等人，2020）进行了比较。结果证明了我们基于因果关系的公平强盗算法在实现在线推荐中个人层面的公平性方面的优势。

实现强盗行为中的反事实公平性

在这一节中，我们将介绍我们的D-UCB和F-UCB匪徒算法。在线推荐通常被建模为一个上下文多臂强盗问题，每个客户都是一个 "强盗玩家"，每个潜在的项目a有一个特征向量a∈A，总共有k个项目1。对于每个在时间t∈[T]到达的顾客，其特征向量xt∈X，算法根据代表用户和物品特征向量（xt，a）串联的向量xt,a推荐具有特征a的物品，观察奖励rt（例如，购买），然后用新的观察结果更新其推荐策略。也可能存在一些中间特征（用I表示），它们受推荐物品的影响，并影响奖励，如用户对相关性和质量的反馈。

通过软干预建立手臂选择模型

在匪徒算法中，我们通常会选择一个使条件奖励期望值最大化的手臂，a_t=arg max_a E[R|x_t,a]。选臂策略可以通过一个从X到A的函数映射来实现，每一轮之后，函数中的参数都会随着最新的观察元组而更新。

我们主张使用因果图和软干预作为任何匪徒算法的一般表示方法。我们考虑因果图G，例如，如图1所示，其中A代表手臂特征，X代表用户特征，R代表奖励，I代表A和R之间的一些中间特征。由于手臂选择过程可以被视为X对A的结构方程，我们将X视为A的父母。然后，奖励R受到手臂选择、上下文用户特征以及一些中间特征的影响，因此所有这三个因素都是R的父母。在这种情况下，很自然地将手臂选择策略的更新视为对手臂特征A进行的软干预π。

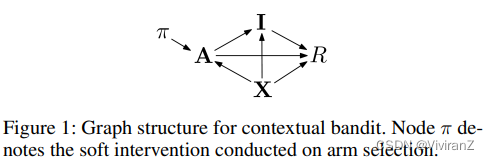
使用软干预建立手臂选择学习模型有几个优点。首先，它可以捕捉到环境和奖励之间复杂的因果关系，而不需要引入强有力的假设，如线性奖励函数，或高斯/伯努利先验分布，这些假设在实践中往往不成立。第二，它在函数形式上是灵活的。例如，它可以是任何函数类型，它可以独立于或依赖于目标变量的现有亲属，也可以包括不是目标变量亲属的新变量。第三，软干预可以是确定性的，即把目标变量固定在一个特定的常数上，也可以是随机性的，即给目标变量分配一个具有多个状态概率的分布。因此，大多数现有的和主要的匪徒算法都可以用这个框架来描述。此外，基于这个框架，我们可以通过采用不同的软干预措施提出新的强盗算法。

形式上，让Πt是时间t∈[T]的手臂选择政策空间，π∈Πt是一个特定的政策。政策π的实施是通过软干预来模拟的。用R(π)表示实施干预后的奖励的非常规值，政策π下的预期奖励，用μπ表示，由E[R(π)|xt]给出。根据σ微积分（Correa and Bareinboim 2020），它可以进一步分解如下。

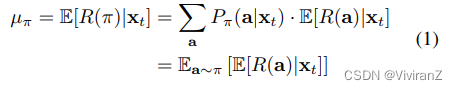
其中Pπ(a|xt)是由策略π定义的分布。请注意，µa代表了选择手臂a时的预期报酬，这仍然是一个干预后的数量，需要用观察分布来表示，以便可以计算。在下文中，我们提出了一种基于d-separation的估计方法，并在此基础上开发了D-UCB算法。为了便于表述，我们在下面的小节中的讨论假定了确定性政策，原则上，上述框架也可以适用于随机性政策。

D-UCB算法

令W⊆A∪X∪I是一个节点子集，该子集将奖励R与因果图中的特征（A∪X）/W分开。这样的集合总是存在的，因为A∪X和P a(R)是trivial的解决方案。让Z=W(A∪X)。使用do-calculus（Pearl 2009），我们可以将µa分解如下。

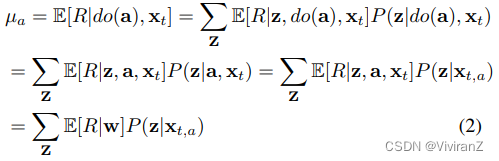
其中最后一步是由于d分离。与(Lu et al. 2020)类似，我们假设根据以前用于建立因果图的知识，分布P(z|xt,a)是已知的。然后，通过使用样本平均数估计器（用μˆw(t)表示）来估计基于截至时间t的观察数据的E[R|w]，估计的奖励平均数由以下公式给出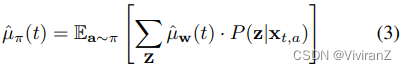

随后，我们提出了一种基于d-separation的因果匪徒算法，称为D-UCB。由于给定一个特定的政策，奖励总是存在不确定性，为了平衡探索和利用，我们在D-UCB算法中遵循面对不确定性的乐观规则（OFU）。在时间t采取的政策将导致预期奖励的最高置信度上限，其结果为

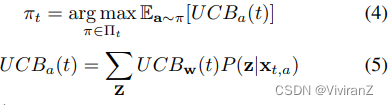
由于µˆw(t)是一个无偏估计值，并且假设奖励的误差项是亚高斯分布，µw(t)的1-δ置信度上限为

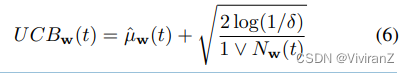
由于µˆw(t)是一个无偏估计，并且假设奖励的误差项为亚高斯分布，µw(t)的1 - δ置信度上限为

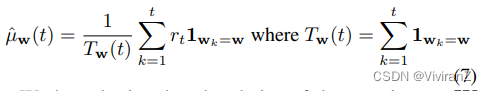
我们假设，d分离集W的选择将显著影响D-UCB的遗憾。为此，我们分析了累积遗憾RT的上界。下面的定理表明，遗憾的上界取决于d-分离集W的域大小。

一个定理：

算法1显示了D-UCB的伪代码。在第2行，根据定理1，我们首先确定具有最小领域空间的d分离集W。在第4行，我们利用因果图和截至时间t的观察数据，找到最佳策略πt = 。在第5行，我们在∼πt处采取行动，并观察到一个实值报酬rt，在第6行，我们用at和rt更新观察数据。

备注:确定最小d分离集在因果推理中已被充分研究（Geiger, Verma, and Pearl 1990）。我们利用寻找最小成本分离器的算法（Tian, Paz, and Pearl 1998）来确定W。发现程序通常需要对因果图有完整的了解。然而，在给定了要使用的d分离集以及相关的条件分布P(z|xt,a)的情况下，算法的其余部分在没有因果图信息的情况下也能正常工作。此外，知道P(z|xt,a)的假设遵循了最近关于因果匪徒的研究工作。将因果强盗框架推广到部分/完全未知的因果图设置是一项更具挑战性但重要的任务。最近的一项工作（Lu, Meisami, and Tewari 2021）试图在因果树/森林结构的基础上泛化因果匪徒算法。

为了更好地说明因果匪徒算法的长期遗憾，假设集合A∪U∪I包括N个与奖励有关的变量，d-separation集合W包括n个变量。如果每个变量都有2个不同的值，那么对于传统的匪徒算法来说，确定性策略的数量可以大到2^N，导致O( √ (2^N*T))的遗憾界限。另一方面，我们提出的因果算法利用了d分离集W的知识，实现了O( √ (2^N*T))的遗憾，这意味着在n<N的情况下，遗憾边界有明显的减少。

反事实的公平

现在，我们准备展示我们公平的UCB算法。我们关注的不是被推荐商品的公平性(例如，小公司生产的商品与大公司生产的商品有相似的被推荐机会)，而是在奖励方面的用户端公平性，即，拥有相似档案的个人用户将获得相似的奖励，无论他们的敏感属性和被推荐的商品，这样他们都能平等地从推荐中受益。为此，我们采用反事实公平作为我们的公平概念。

假设用户的个人资料中有一个敏感属性S∈X。反事实公平关系到假设个体处于不同的敏感群体中，个体将获得的预期奖励。在我们的语境中，这可以被表述为反事实奖励E[R(π， s∗)|xt]，其中同时执行两种干预:软干预对手臂选择的π和硬干预对敏感属性s的∗，同时对个体特征xt进行条件反射。对奖励的反事实效应记作，反事实公平的策略定义如下。

定义3：如果∆π = 0，则政策π对于到达的个体是反事实公平的。如果|∆π|≤τ，其中τ是预定义的公平阈值，则策略为τ -反事实公平。

为了实现在线推荐中的反事实公平，在第t轮时，我们只能从客户(具有x_t特性)的臂子集中选取arm，其中所有臂都满足反事实公平约束。公平策略子空间Φ_t⊆Π_t由Φ_t = {π:∆_π≤τ}给出。

然而，反事实公平是一个因果量，在没有结构方程知识的情况下，观测数据不一定无法识别(Shpitser和Pearl 2008)。Wu, Zhang和Wu(2019)研究了给定因果图的反事实公平性的识别准则，并给出了不可识别的反事实公平性的边界。根据(Wu, Zhang, and _u 2019)中的命题1，如果X{S}不是S的后代，我们的反事实公平性是可识别的。在这种情况下，类似于公式(1)，我们得到E[R(π，S∗)|x_t] = E_{a ~ π}[E[R(a, S∗)|x_t]]其中S∗∈{S +， S−}。与Eq.(2)相似，我们表示µa,s∗= E[R(a, s∗)|xt]，它可以被用do-calculus分解为：

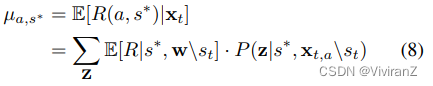
其中w∗={s∗ ，ws_t}，μˆ_{w∗}(t）也是基于截至时间t的观察数据的样本平均估计。一项政策的估计反事实差异为：

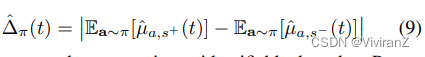
在µa,s∗无法识别的情况下，基于（Wu, Zhang, and Wu 2019）中的命题2，我们推导出µ_{a,s∗}的下限和上限，如下定理所示。

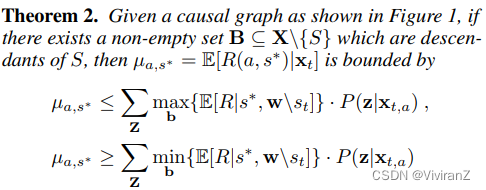
F-UCB算法

考虑到反事实差异的估计误差，我们也可以使用反事实效应的高概率置信度上限来建立保守的公平政策子空间Φ¯ t = {π : UCB_{∆π}(t) ≤ τ}，其中

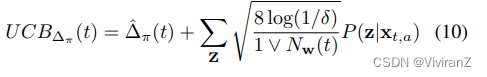
这是根据两个独立的亚高斯随机变量之和仍然是亚高斯分布这一事实得出的。因此，学习问题可以被表述为以下受限的优化问题:

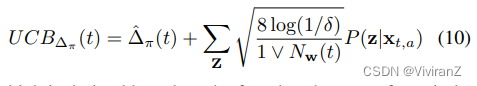
其中π ∗ t被定义为每轮政策空间Π_t中的最优政策，这在D-UCB设置中是相同的。附录中的假设3给出了安全策略π0的定义，它指的是每轮公平策略子空间下的可行方案，即π0∈Πt，使∆_{π0}≤tao，对于每个t∈[T]。
这个优化可以通过遵循OFU的规则类似地解决。算法2描述了我们称为F-UCB的公平强盗算法。与D-UCB算法不同，F-UCB在每个时间t只从Φ¯ t中挑选手臂。在第5行，我们计算估计的奖励平均值和估计的公平差异。在第6行，我们确定公平策略子空间Φ¯ t，在第7行，我们找到最佳策略πt =

下面的遗憾分析表明，F-UCB的遗憾边界比D-UCB的遗憾边界要大，正如预期的那样，它仍然受到集合W的域大小的影响。

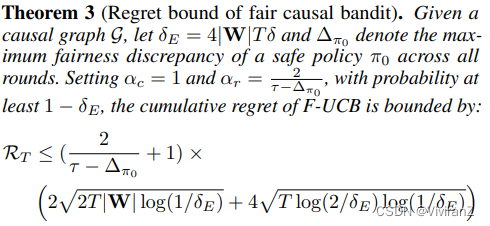
备注:在定理3中，αc和αr指的是分别控制与奖励和公平项有关的样本平均估计值的置信区间大小的尺度参数。在（Huang, Zhang, and Wu 2021）的附录中，我们展示了αc和αr应该满足的数字关系，以便同步约束误差项引起的不确定性。定理3中的取值是一个可行的解决方案，αc在约束域空间下取最小值。

我们提出的一般框架（公式（1））可以适用于任何政策/函数类。然而，我们提出的D-UCB和F-UCB算法仍然采用经典UCB算法之后的确定性策略。因此，的构造可以很容易实现，因为政策的总数是有限的。在本文中，我们还假设了离散变量，但原则上，所提出的算法也可以通过采用某些近似方法扩展到连续变量，例如，估计概率的神经网络和估计积分的抽样方法。然而，遗憾边界分析可能不适用，因为|W|在连续空间中会变得无限大。

【后期补一下，这次大概了解了做什么的：通过引入软干预（一种比较新的干预的升级版操作），RL可以变得更好；还证明了（d-seperation&最小子集）】

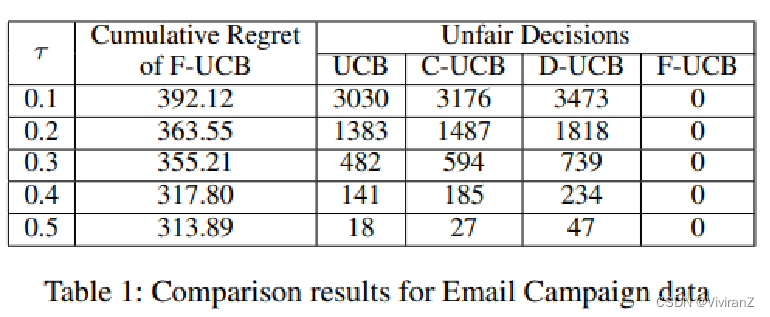
表1显示了F-UCB（T=5000回合）的累积遗憾是如何随公平性阈值τ变化的。表1（和表2）中的数值是通过对5次试验的结果进行平均得到的。τ越大，累积遗憾越小。在表1的右边部分，我们进一步报告了其他三种算法在T=5000轮的探索过程中违反公平性的次数，这表明了公平性意识的匪徒的必要性。相比之下，我们的F-UCB在每一轮都实现了严格的反事实公平性。

【实验部分待补】

结论

在我们的论文中，我们研究了如何通过在bandits中加入因果推理来连续学习最佳干预。我们开发了D-UCB和F-UCB算法，这些算法利用了从基础因果图中确定的d-separation集，并采用软干预来模拟手臂选择策略。我们的F-UCB通过从满足反事实公平性约束的武器子集中选择武器，进一步实现了每轮探索中的反事实个体公平性。我们的理论分析和实证评估显示了我们的算法对基线的有效性。