强化学习笔记：多臂老虎机问题(3)--行动价值估计的增量实现0. 前言1. Incremental Implementation

86 阅读 0 评论 57 点赞

我是靠谱客的博主个性画笔，最近开发中收集的这篇文章主要介绍强化学习笔记：多臂老虎机问题(3)--行动价值估计的增量实现0. 前言1. Incremental Implementation，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

0. 前言

1. Incremental Implementation

0. 前言

前情概要参见：

强化学习笔记：多臂老虎机问题（1）https://blog.csdn.net/chenxy_bwave/article/details/121395855https://blog.csdn.net/chenxy_bwave/article/details/121395855

强化学习笔记：多臂老虎机问题(2)--Python仿真https://blog.csdn.net/chenxy_bwave/article/details/121472838https://blog.csdn.net/chenxy_bwave/article/details/121472838

本节我们继续上一篇的话题，考虑如何以更高效的方式实现行动价值Q的估计。

1. Incremental Implementation

在前面的action-value方法中我们估计行动价值Q采用的是sample-average方法，即简单的样本平均。考虑Ri为第i次选择行动a所得到的奖励，并记Qn为已经有(n-1)次采取了行动a后对行踪a的价值估计值，则行动价值估计公式可以简化为（注意，因为这里只考虑行动a了，所以比前面的公式要更简单了）：

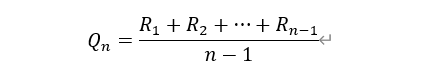
如果按照这个基本式来计算的话，每次采取行动a并重新估计对应的行动价值的时候需要对到当前为止的所有的对应于行动a的奖励求平均，这进一步要求将到当前为止的每一步奖励都保存下来。随着时间的推进，所需要保存的历史奖励和所需要的求样本平均的计算量都越来越大。这显然不能说是一种有效的实现方式，甚至不能说是一种可行的实现方式。考虑极端的情况，当游戏时间无限延申时，对存储和计算的需求都将变得无限大，因而没有实现可行性。所以我们需要考虑一种高效的可行的实现方式。

将上式进行如下所示的简单变形：

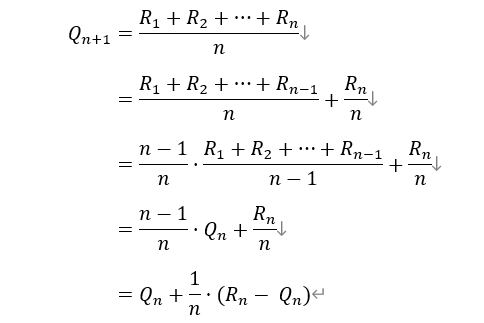
由此，我们得到一个关于行动价值估计计算的递推关系式。Q1为初始值表示对于该行动价值估计的先验估计，可以初始化为任何值，因为事实上它不影响后续的估计。用n=2代入上可知，Q2=R1，Q3=（R1+Q2）/2, 很显然它们跟Q1没有关系。

在Sutton-book中被称之为Incremental Implementation(增量式实现)，这种方式的处理在后面我们会频繁地碰到。在这一实现方式中，不需要记忆历史奖励数据，而且每次Q值更新计算的运算量是恒定不变的。这一递推更新计算方式的一个通用形式是：

NewEstimate <-- OldEstimate + StepSize*[Target - OldEstimate]

[Target - OldEstimate]表示当前估计值与目标值的差距或者说估计误差项。为了使估计值更接近目标，调节量由这个误差乘以一个系数StepSize(通常小于1)得到。在以上行动价值估计递推关系式中，Target其实是当前得到的奖励R(n)，而StepSize则是(1/n).

基于以上递推关系，我们可以重新改写行动价值估计的代码，如下所示：

Q[a[t]] = Q[a[t]] + (r[t]-Q[a[t]])/aNum[a[t]]

需要注意的是，上面推导时只考虑一个行动。但是实际代码实现中需要对K个行动进行跟踪，所以代码比上面的递推关系式要显得更复杂一些。每次只针对当前时刻所采取的行动更新其行动价值估计，Q值以及行动被选择的次数都需要针对K个行动分别存储更新。

下一篇我们将继续学习“Tracking a Nonstationay Problem”.参见：强化学习笔记：多臂老虎机问题(4)--跟踪非平稳环境https://blog.csdn.net/chenxy_bwave/article/details/121630186https://blog.csdn.net/chenxy_bwave/article/details/121630186

Ref: Sutton-RL-book section2.4