蓝牙AOA到达角算法（二）

蓝牙AOA到达角算法（二）

今天我们继续接着上一篇文章，继续介绍奔骝定位的高精度定位系统：蓝牙AOA到达角算法，本篇的主要工作是介绍其中的数学基础，系列文章的第二篇主要集中在高数部分，因为没有对应的数学基础，是没有办法深入了解清楚的。

最先我们要清楚的是复数概念，设C为复数，a、b为实数，常数形式的复数C=a+jb,其中a是实部，b是虚部；或者可以表示为C=|c|ejß,其中|C|=a2+b2,这个是他的摸，而tanß=b/a，ß也称为复数的辐角。

了解了复数之后，我们需要的积累是蓝牙AOA所得到的信号为复指数信号，所谓复指数信号就是指数部分为复数。F(t)=Kest,其中s是复数，设s=ơ+jw，根据欧拉公式，可以将复指数信号展开为f(t)=Kest=ke(ơ+jw)t=keơtcos(wt)+jeơtsin(wt)。

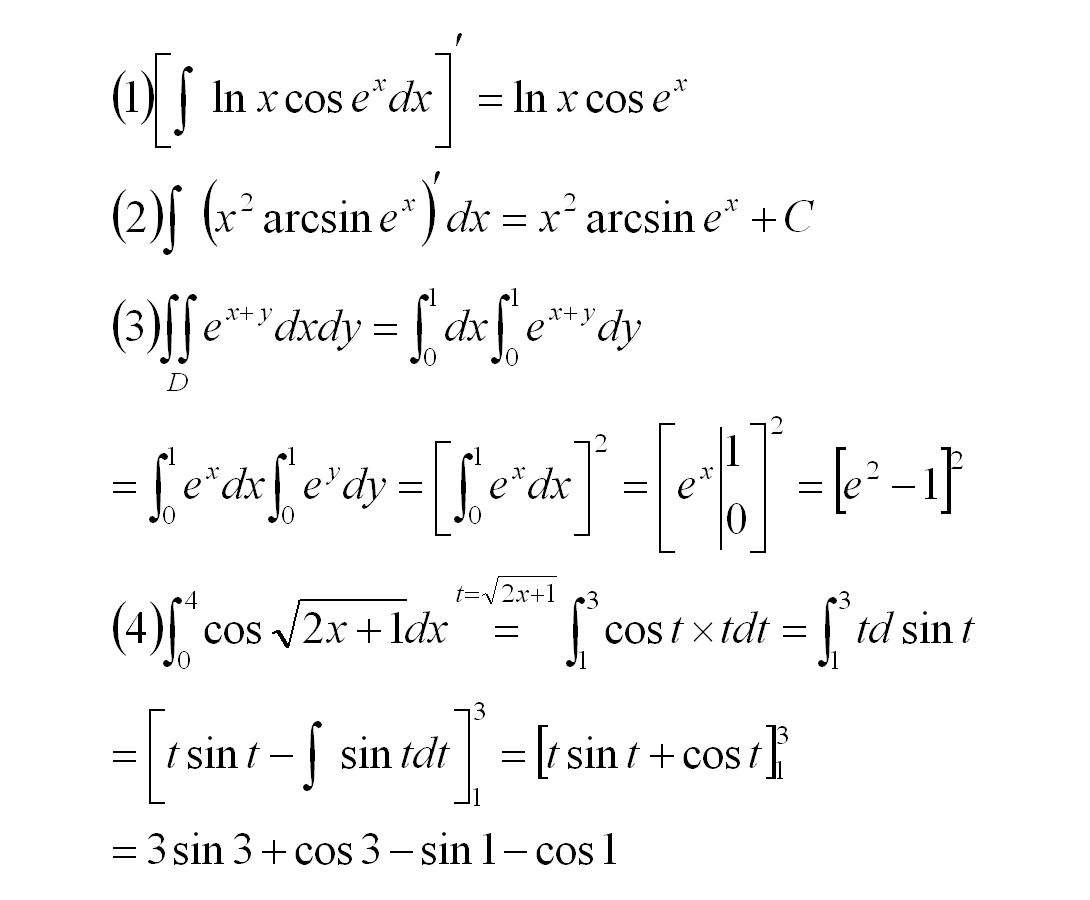
回到高数本身，首先我们需要建立的思想是极限的思想，比如计算圆的面积，不断地分割圆为多边形，使用可计算的多边形的面积来不断逼近圆的面积。

第二点就是学会导数的应用，导数简而改之就是在函数上某一点的变化率，找到了变化率，就可以找到函数某点的变化趋势。结合我们定位系统，比如某个定位对象在移动过程中，我们将定位对象的位置（可以简单描述为坐标点）和时间建立一个函数关系，那么这个函数上某个点的变化率，也就是时间刻度上的变化率就是移动加速度，这个移动速度可以在定位系统中用来分析定位对象的位置移动是否异常，行为是否异常等。

接着出场的自然就是微分概念，微分就是在函数某一点的极限变化量。继续使用定位系统来阐述，上一段中的函数关系中的某时刻的微分，可以理解为位置移动的速度。这个速度十分有用，因为我们的位置测量经常会出现误差，那么我们使用这个速度来修正坐标的改变，其中比较著名的算法是卡尔曼滤波。

第四部分需要建立的概念是积分概念，其实积分概念是紧跟着极限概念和微分的，我们计算某些函数值时，是没有办法精确计算的，可以采用近似计算，而这个近似计算的工具常常是积分，近似计算的积分范围如果取的好，那么所产生的误差可以和测量值相差比较大，那么这部分误差就可以忽略不计。

有了导数、微分和积分的基础之后，很多现实中的问题就可以转换为微积分问题，当然这个世界还是比较复杂的，很多并不是两两的函数关系，这个时候，我们就要学会使用降阶和多重积分，也就是把复杂问题不断分解，自然也就有了全微分，多重积分等。

不过在我们研究定位系统，特别是定位系统算法，当然包括本篇我们阐述的蓝牙AOA到达角算法的时候，高数只是工具，我们需要的是看得懂，因为很多前辈已经做了很多现成的算法，我们要做的是拿来应用和更新。

最后

以上就是失眠发夹为你收集整理的蓝牙AOA到达角算法（二）的全部内容，希望文章能够帮你解决蓝牙AOA到达角算法（二）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。