数据分析_学习笔记

77 阅读 0 评论 51 点赞

我是靠谱客的博主虚心小熊猫，最近开发中收集的这篇文章主要介绍数据分析_学习笔记，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

第一章: 描述性统计分析

1.1 概念

1.1.2 描述性统计所提取统计的信息,我们称为统计量,主要包括以下几个方面:

频数和频率

频率,指每个类别变量的频数与总次数的比值,通常采用百分数表示.

集中趋势分析:均值,中位数,众数,分位数

均值:平均值

中位数:将一组数据升序排列,位于该组数据最中间位置的值,就是中位数.如果数据为偶数,为中间两个数的均值.

众数:一组数据中出现次数最多的值

分位数:通过n-1把一组数据分为n个区间,是的每个区间的数值个数相等(或近似相等),其中n为分位数的数量,常用的分位数有四分位数与百分位数.已四分位为例,计算分位数.

1,首先,计算四分位的位置:Q1_index = (n-1)*0.25; Q2_index=(n-1)*0.5; Q3_index=(n-1)*0.75.

2,如果四分位的位置与数据的位置重合,四分位等于四分位的位置对应的数值;如果四分位的位置与数据的位置不重合,按最近位置的两个数据,以加权计算的方式得到四分位的位置,权重为距离的反比.

Numpy中计算分位数

x = np.arange(10,20)
n = len(x)
#计算四分位的索引(index)
q1_index = (n-1)*0.25
q2_index = (n-1)*0.5
q3_index = (n-1)*0.75
print(q1_index,q2_index,q3_index)
index = np.array([q1_index,q2_index,q3_index])
#计算左边和右边元素的值
left = np.floor(index).astype(np.int32)
right = np.ceil(index).astype(np.int32)
#获取index的小数部分与整肃部分
weight,_ = np.modf(index)
#根据左右两边的整数,加权计算四分位数的值,权重与距离成反比.
q = x[left]*(1-weight) + x[right]*weight

plt.figure(figsize=(15,4))
plt.xticks(x)
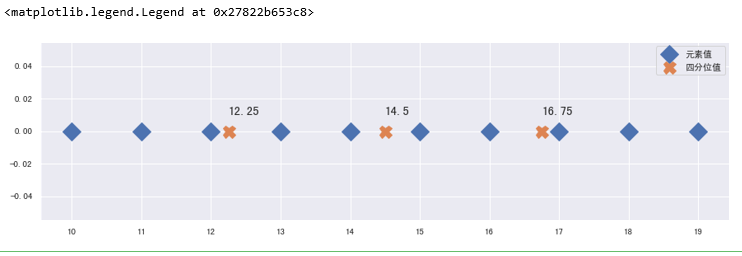
plt.plot(x,np.zeros(len(x)),ls="",marker="D",ms=15,label="元素值")
plt.plot(q,np.zeros(len(q)),ls="",marker="X",ms=15,label="四分位值")
for v in q:
plt.text(v,0.01,s=v,fontsize=15)
plt.legend()

离散程度分析:极差,方差,标准差

极差:极差指一组数据中最大值与最小值的差;

方差:体现的是一组数据中,每个元素与均值偏离的大小.

标准差:标准差为方差的开方

分布形状:偏度,峰度

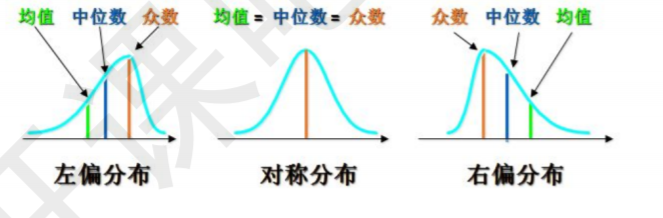
偏度是统计数据分布偏斜方向和程度的度量,是统计数据分布非对称程度的数字特征.

如果数据对称分布(e.g.正态分布),则偏度为0

如果数据左偏分布,则偏度小于0,右偏分布,偏不大于0.

Numpy 构造分布数据

#构造左偏分布数据
t1 = np.random.randint(1,11,size=100)
t2 = np.random.randint(11,21,size=500)
t3 = np.concatenate([t1,t2])
left_skew = pd.Series(t3)
# print(left_skew)
#构造右偏分布数据
t1 = np.random.randint(1,11,size=500)
t2 = np.random.randint(11,21,size=100)
t3 = np.concatenate([t1,t2])
right_skew = pd.Series(t3)
#计算偏度
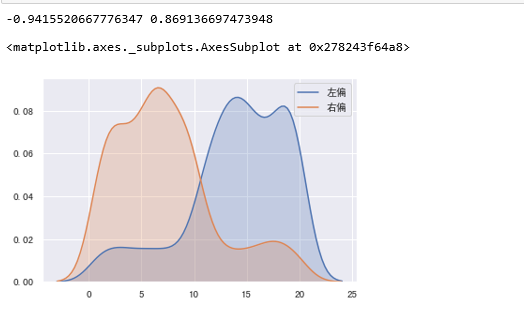
print(left_skew.skew(),right_skew.skew())
#绘制核密度图
sns.kdeplot(left_skew,shade=True,label="左偏")
sns.kdeplot(right_skew,shade=True,label="右偏")

峰度:峰度是描述总体中所有取值分布形态陡缓程度的统计量.可以将峰度理解为数据分布的高矮程度,峰度的比较是相对于标准正态分布的.

对于标准正态分布,峰度为0.

如果峰度大于0,则密度图高于标准正态分布.数据在分布上比标准正态分布密集,方差较小.

如果峰度小于0,则密度图低于标准正态分布,数据在分布上比标准正态分布分散,方差较大.

Numpy 示例峰度

#标椎正态分布
standard_normal = pd.Series(np.random.normal(0,1,size=10000))
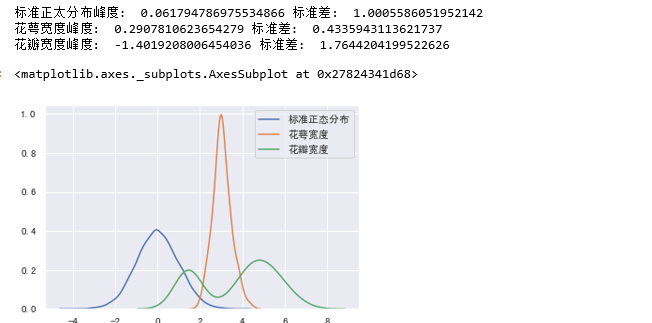
print("标准正太分布峰度: ",standard_normal.kurt(),"标准差: ",standard_normal.std())
print("花萼宽度峰度: ",data["sepal_width"].kurt(),"标准差: ",data["sepal_width"].std())
print("花瓣宽度峰度: ",data["petal_length"].kurt(),"标准差: ",data["petal_length"].std())
sns.kdeplot(standard_normal,label="标准正态分布")
sns.kdeplot(data["sepal_width"],label="花萼宽度")
sns.kdeplot(data["petal_length"],label="花瓣宽度")