1.计算（=信息处理）

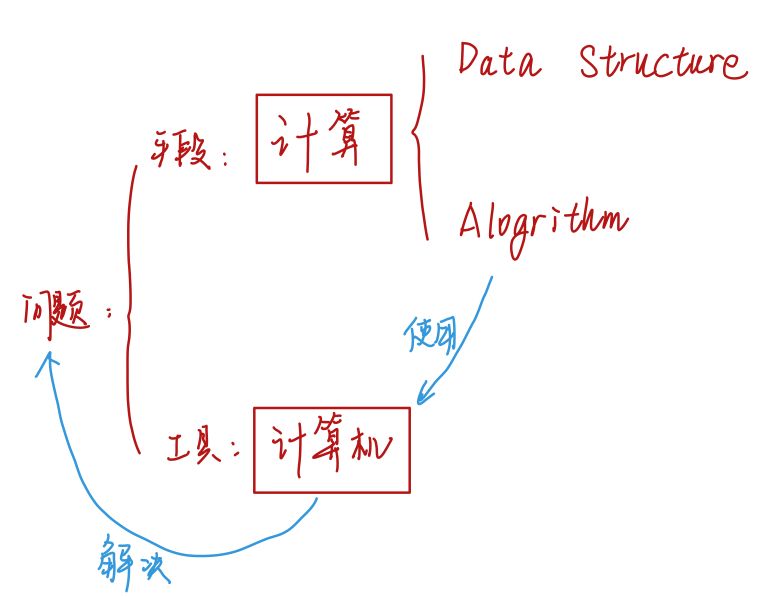
如果我想解决一个问题，那么计算机是我用来解决问题的工具而计算则是我的手段。如我借助工具为我解决问题时，得用一些手段才能使工具发挥作用。

计算的对象：有规律和技巧可循
计算的目标：高效和低耗
计算的构成=Data Structure（数据结构）+Algorithms（算法）

算法:是指在特定的计算模型下，旨在解决特定问题的指令序列。如我有双筷子，我用它吃饭，夹这个动作就是算法。

好算法:正确健壮可读效率

2.计算模型（=计算机=信息处理工具）

2.1 TM

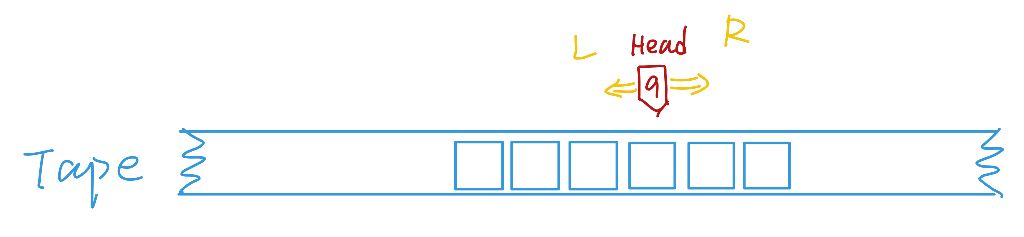
Turing Machine图灵机模型

Transition Function：(q,c;d,L/R,p)

(若状态为q的字符为c，将c改写为d；然后转向左侧/右侧的邻格；转入p状态，一旦p为’h’，则停机

2.2 RAM

Random Access Machine随机存取器模型只支持+ -操作，且不允许对常数进行

寄存器R[i]：总数没有限制

3.大O记号

什么是渐进分析？就是对于问题规模的逐渐增加，对计算成本的分析
T(n):需执行的基本操作次数
S(n):需占用的存储单元（一般可不考虑）

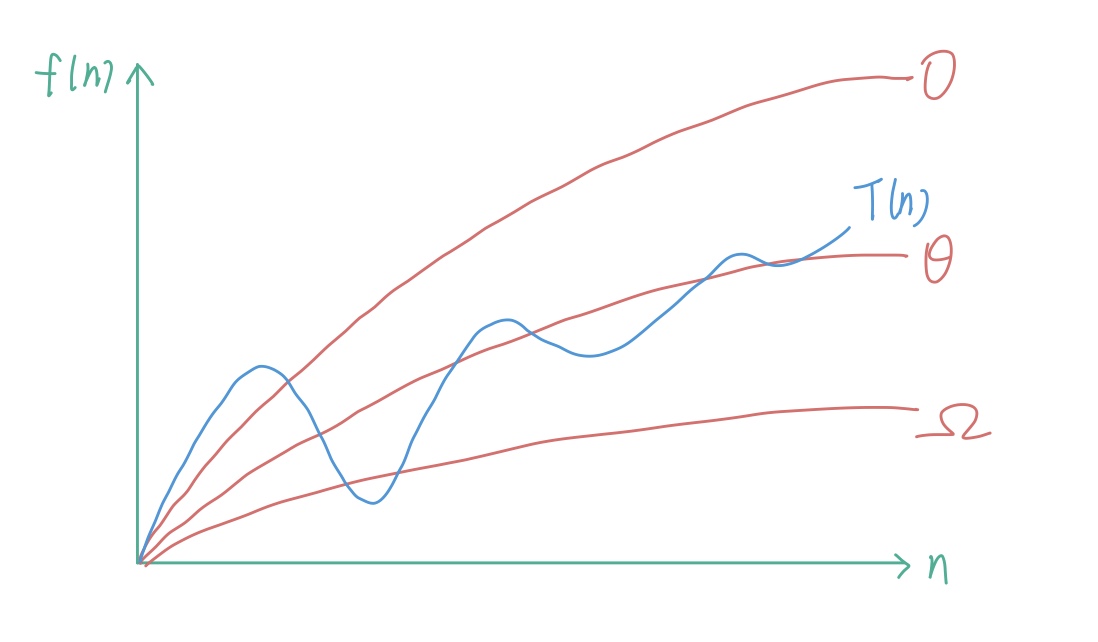
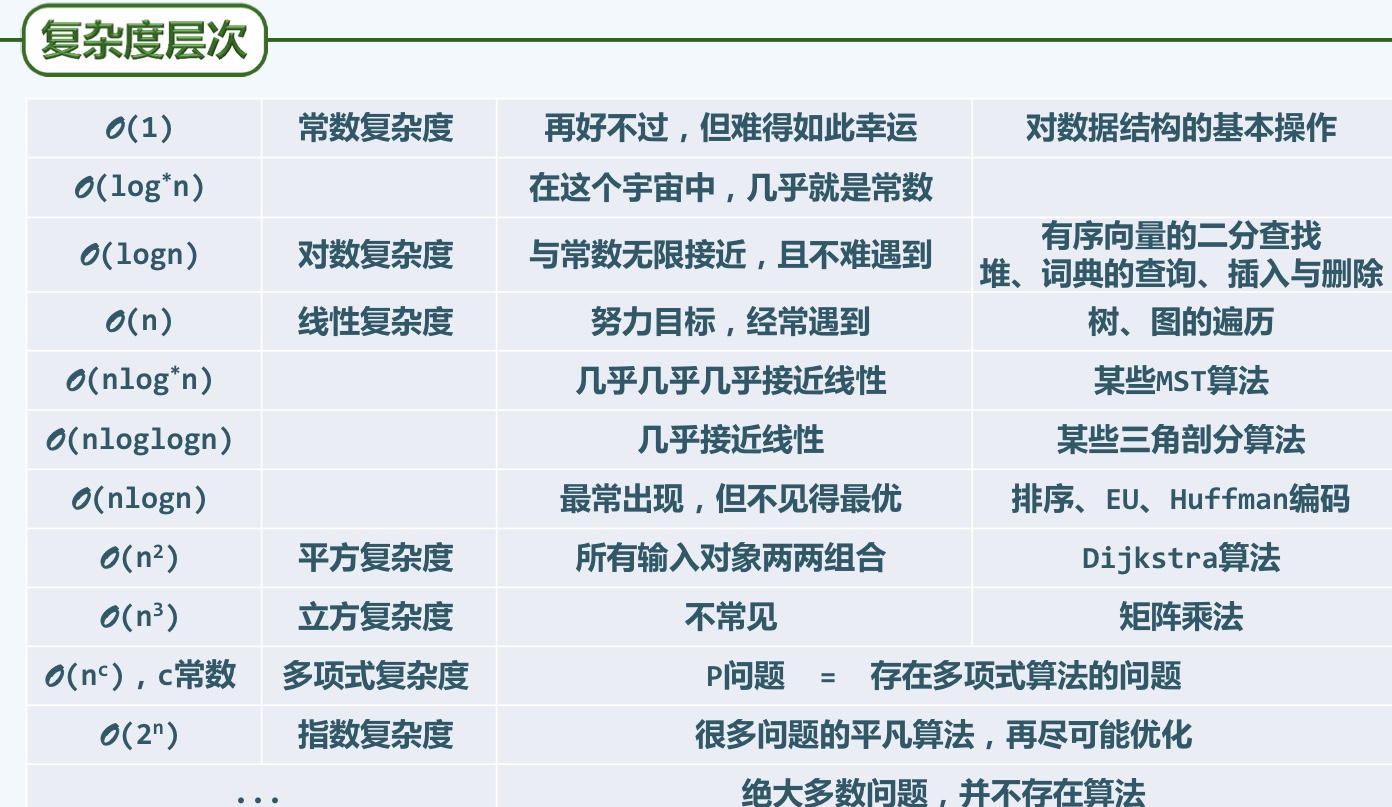
O(f(n))常用的几个刻度

O(1) O(log^cn) O(n^c) O(2ⁿ)

4.算法分析

4.1 正确性

不变性+单调性

以起泡排序为例

void bubblesort(int A[],int n){	
	for(bool sorted=false;sorted=!sorted;n--)//这里很巧妙的用bool标志是否有序
		for(int i=1;i<n;i++)
			if(A[i]<A[i-1]{
				swap(A[i-1],A[i];
				sorted=false;//执行交换说明存在逆序，标志转为false
			}
}

分析：
不变性：经k轮扫描交换，最大的k的元素必然就位
单调性：经k轮扫描交换，问题规模缩减至n-k
正确性：经至多n趟扫描算法必然终止并给出正确解答

4.2 复杂度

（1）迭代：级数求和
算术级数: 与末项平方同阶
幂方级数: 比幂次高出一阶
几何级数: 与末项同阶
收敛级数: O(1)
调和级数: θ(logn)
对数级数: θ(nlogn)

（2）递归：递归跟踪+递推方程
递归跟踪：检查每个递归实例累计所需时间
递推方程：列出递推方程求解

（3）猜测+验证
Back-Of-The-Envelope Calculation封底估算：一天=10⁵sec 三生三世=10¹⁰sec

5.迭代与递归

5.1 数组求和

1.迭代：显然复杂度为O(n)，且θ(n)，Ω(n)

int sum1(int a[],int n){	
 int sum=0;
 for(int i=0;i<n;i++){
  sum+=a[i];
 }
 return sum;
} 

2.线性递归：

减而治之Decrease-and-conquer：把问题分成两个子问题：平凡+规模缩减

这里的平凡是A[n-1]

int sum2(int A[],int n){
 return (n<1)? 0:sum2(A,n-1)+A[n-1];
} 

复杂度分析：
（1）递归跟踪（列出每个实例）：O(n)
（2）递推方程：T(n)=T(n-1)+O(1)=O(n)

3.二分递归：

分而治之Divide-and-conquer:把问题划分成规模大体相当的若干子问题（一般为两个）：子问题+子问题+子问题+…

这里分成了两个字问题，即把一个数组分成两半

int sum3(int a[],int low,int high){
 if(low==high) return a[low];//递归基
 int middle=(low+high)/2;
 return sum3(a,low,middle)+sum3(a,middle+1,high);
}

复杂度分析：
（1）递归跟踪：O(n)

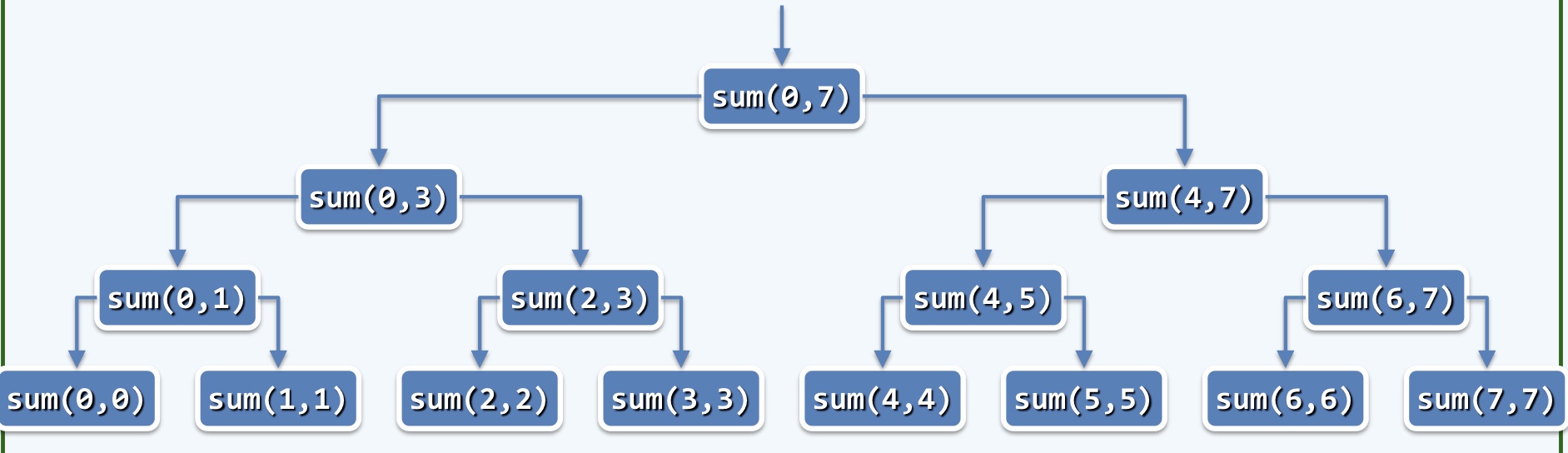
（2）递推方程：T(n)=2*T(n/2)+O(1)=O(n)

5.2 数组倒置

1.迭代
（1）原始版

next:
if(lo<hi){swap(A[lo],A[hi];lo++;hi--;goto next;}

（2）精简版

while(lo<hi) swap(A[lo++],A[hi--];

2.递归
接口：void reverse(int *A,int lo,int hi)

if(lo<hi){swap(A[lo],A[hi]);reverse(A,lo+1,hi-1);}

5.3 找出最大两个整数

1.迭代：O(2n-3)
（1）先找出最大的，再在剩余的元素中找出第二大的

void max2_1(int a[],int low,int high,int &x1,int &x2){//迭代1 
 x1=low;
 for(int i=low+1;i<high;i++)//找出最大值 
  if(a[x1]<a[i]) x1=i;
 x2=low;
 for(int i=low+1;i<x1;i++)//在[low，x1）之间找出次大值 
  if(a[x2]<a[i]) x2=i;
 for(int i=x1+1;i<high;i++)//在（x1+1，high）之间找出次大值 
  if(a[x2]<a[i]) x2=i;
 cout<<"迭代1:"<<"zui: "<<a[x1]<<" ci:"<<a[x2]<<endl;
}

（2）先把数组前两个数的编号分别比较大小后赋值给最大的和次大的，在后面的遍历中每次先与次大的比较，如果比次大的大，则先把编号赋给次大的再与最大的比较，若大于最大的则交换

void max2_2(int a[],int low,int high,int &x1,int &x2){//迭代2 
 if(a[x1=low]<a[x2=low+1]) swap(x1,x2);
 for(int i=low+2;i<high;i++){
  if(a[x2]<a[i])//先与次大的比较
   if(a[x1]<a[x2=i])//如果比次大的大，则先把编号赋给次大的再与最大的比较,若大于最大的
    swap(x1,x2);//则交换
 }  
 cout<<"迭代2:"<<"zui: "<<a[x1]<<" ci:"<<a[x2]<<endl;
}

2.递归+分治
把数组分成两半，分别在其中找出最大值和次大值，然后再从找出来的值中比较

void max2_3(int a[],int low,int high,int &x1,int &x2){//递归+分治 
 if(low+2==high){//两个元素比较 
  if(a[x1=low]<a[x2=high-1]) swap(x1,x2);
  return;    
 }
 if(low+3==high){//三个元素比较 
  int mid=(low+high)/2;
  if(a[low]<a[mid]&&a[high-1]<a[mid]) {
   x1=mid;
   x2=(a[low]<a[high-1])?high-1:low;
  }
  else if(a[low]>a[mid]&&a[low]>a[high-1]){
   x1=low;
   x2=(a[mid]<a[high-1])?high-1:mid;
  }
  else{
   x1=high-1;
   x2=(a[low]<a[mid])?mid:low;
  }
  return;
 }
 int middle=(low+high)/2;
 int x1l,x2l;
 max2_3(a,low,middle,x1l,x2l);
 int x1r,x2r;
 max2_3(a,middle,high,x1r,x2r);
 if(a[x1l]>a[x1r]) {
  x1=x1l;
  x2=(a[x1r<a[x2l]])?x2l:x1r;
 }
 else {
  x1=x1r;
  x2=(a[x1l<a[x2r]])?x2r:x1l; 
 }

测试：

int main(){
 int a[]={3,5,4,2,1,6,9,8,7};
 int x1=0,x2=0;
 max2_1(a,0,9,x1,x2);
 max2_2(a,0,9,x1,x2);
 max2_3(a,0,9,x1,x2);
 return 0;
}

测试结果：

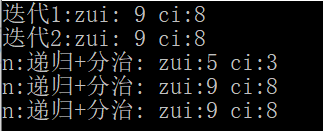
说明：递归加分治结果：第一行是第一次分治的左侧的结果，第二行是第一次分治的右侧的结果

典型的递推方程

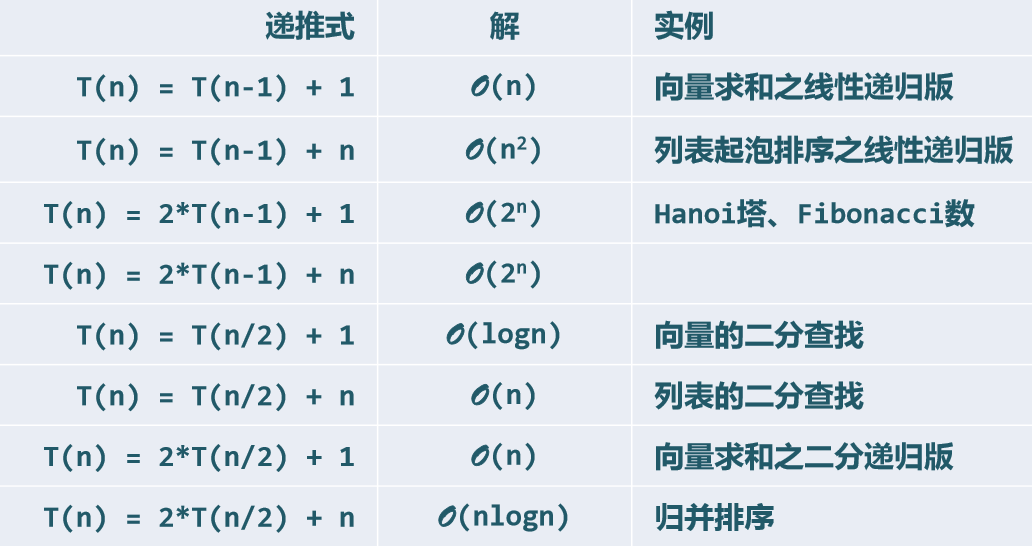
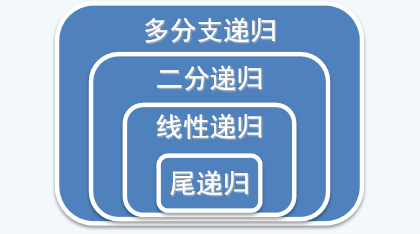
递归关系

尾递归-就是递归在最后一步
线性递归–减而治之
二分递归–分而治之

6.动态规划

6.1 Fibonacci

1.递归：T(n)=O(2ⁿ),S(n)=O(n)

int fib_1(int n){//递归 
return (n<2)?n:fib_1(n-1)+fib_1(n-2); 
}

递归跟踪：可以看出有大量重复，怎么办呢，可以换个角度：自下而上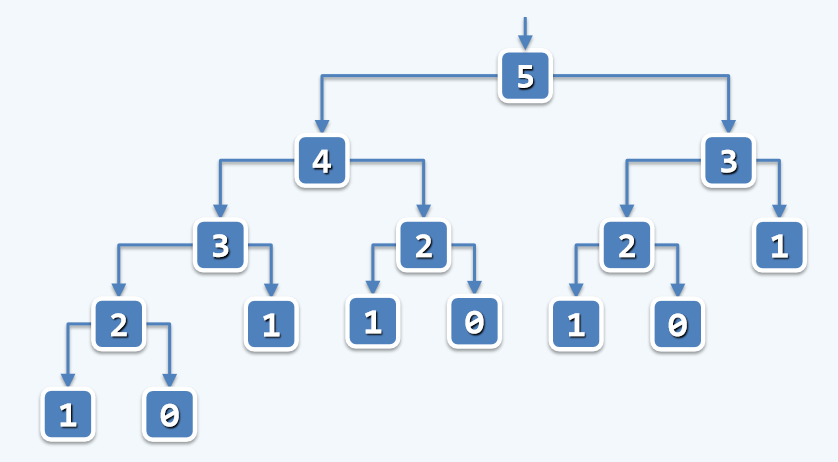
2.迭代:T(n)=O(n),S(n)=O(1)

int fid_2(int n){//迭代  
	int f=0,g=1;  
	if(n==0) return 0;  
	else{   
		while(1<n--){    
			g=g+f;    
			f=g-f;  
		 }   
		 return g;    
	} 
}

6.2 Longest Common Sequence

1.递归：减而治之

inline string max(string a,string b){
 return a.length()<b.length()?b:a;
}
inline int max(int a,int b){
 return a<b?b:a;
}
string LCS_1(string A, string B){//递归 
 cout<<A<<"t"<<B<<endl;
 int len_A = A.length();
 int len_B = B.length();
 cout<<len_A<<"t"<<len_B<<endl;
 //字符串为空时 
 if(len_A==0||len_B==0) 
  return "result:";
 //字符串最后一个字母一样时 
 else if(A.back()==B.back()) 
  return LCS_1(A.substr(0,len_A-1),B.substr(0,len_B-1))+A.back();
 //字符串最后一个字母不一样时 
 else{
  return max(LCS_1(A.substr(0,len_A),B.substr(0,len_B-1)),LCS_1(A.substr(0,len_A-1),B.substr(0,len_B)));
 } 
}

2.迭代：
减而治之：相同时二维数组取左上角单元数加1
分而治之：取上方或左侧更大者

void LCS_2(string A, string B){//迭代 
 int len_A = A.length();
 int len_B = B.length();
 int array[len_A+1][len_B+1];
 //初始化二维数组 
 for(int i=0;i<len_A+1;++i){
  for(int j=0;j<len_B+1;++j){
   array[i][j]=0;
  }
 }
 //记录 
 for(int i=1;i<len_A+1;i++){
  for(int j=1;j<len_B+1;j++){
   if(A[i-1]==B[j-1])
    array[i][j]=array[i-1][j-1]+1;
   else
    array[i][j]=max(array[i-1][j],array[i][j-1]);
  }
 }
 //输出记录表 
 for(int i=0;i<len_A+1;++i){
  for(int j=0;j<len_B+1;++j){
   cout<<array[i][j]<<"t";
  }
 cout<<endl;
 }
 //输出结果 
 for(int i=1;i<len_A+1;i++){
  for(int j=1;j<len_B+1;j++){
   if(A[i-1]==B[j-1])
    //观察二维数组可得
    if(array[i][j-1]<array[i][j+1]&&array[i-1][j]<array[i+1][j]&&array[i][j]!=array[i+1][j-1]) 
     cout<<A[i-1]<<" ";
  }
 }
}

二维数组表图例：

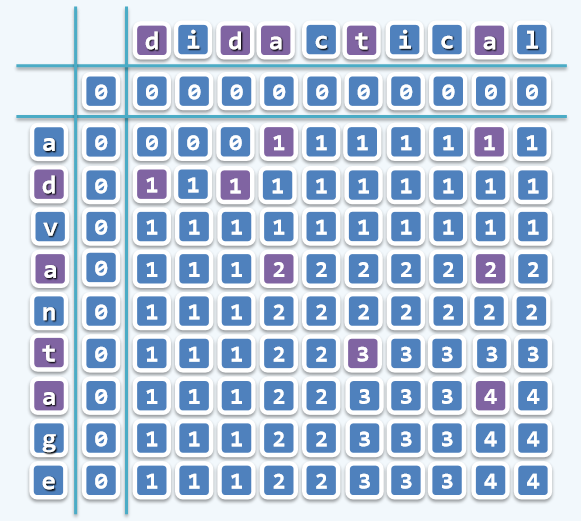
最后

以上就是高贵果汁为你收集整理的《数据结构》学习笔记-第一章 绪论（需反复揣摩）1.计算（=信息处理）2.计算模型（=计算机=信息处理工具）3.大O记号4.算法分析5.迭代与递归6.动态规划的全部内容，希望文章能够帮你解决《数据结构》学习笔记-第一章 绪论（需反复揣摩）1.计算（=信息处理）2.计算模型（=计算机=信息处理工具）3.大O记号4.算法分析5.迭代与递归6.动态规划所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。