机器学习面试题解（1-5）

1、L1正则和L2正则的区别
先放上一个参考博客
https://blog.csdn.net/jinping_shi/article/details/52433975

要点：

1. 线性回归中加入两个不同的正则分别就是两个不同的回归
2. L1和L2正则的定义
   
3. L1和L2正则化的主要作用
   

知道定义和作用基本上可以回到上面的问题了。如果希望有更加深入的理解的，可以点击我们最先放出来的参考链接，查看更加详细地内容。

L2正则化和过拟合
拟合过程中通常都倾向于让权值尽可能小，最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程，若参数很大，那么只要数据偏移一点点，就会对结果造成很大的影响；但如果参数足够小，数据偏移得多一点也不会对结果造成什么影响，专业一点的说法是『抗扰动能力强』。

ps：关于正则化，如果问到更加细致的问题，希望大家能够去认真看一下我放出的参考博客。

2、哪些机器学习不需要归一化
在实际应用中，通过梯度下降法求解的模型一般都是需要归一化的，比如线性回归、logistic回归、KNN、SVM、神经网络等模型。

但树形模型不需要归一化，因为它们不关心变量的值，而是关心变量的分布和变量之间的条件概率，如决策树、随机森林(Random Forest)。

其他如管博士所说，我归一化和标准化主要是为了使计算更方便 比如两个变量的量纲不同 可能一个的数值远大于另一个那么他们同时作为变量的时候 可能会造成数值计算的问题，比如说求矩阵的逆可能很不精确 或者梯度下降法的收敛比较困难，还有如果需要计算欧式距离的话可能 量纲也需要调整 所以我估计lr 和 knn 标准化一下应该有好处。
至于其他的算法 我也觉得如果变量量纲差距很大的话 先标准化一下会有好处。

3、逻辑斯特回归为什么要对特征进行离散化
作者：知乎用户
链接：https://www.zhihu.com/question/31989952/answer/54184582
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

在工业界，很少直接将连续值作为逻辑回归模型的特征输入，而是将连续特征离散化为一系列0、1特征交给逻辑回归模型，这样做的优势有以下几点：0. 离散特征的增加和减少都很容易，易于模型的快速迭代；1. 稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展；2. 离散化后的特征对异常数据有很强的鲁棒性：比如一个特征是年龄>30是1，否则0。如果特征没有离散化，一个异常数据“年龄300岁”会给模型造成很大的干扰；3. 逻辑回归属于广义线性模型，表达能力受限；单变量离散化为N个后，每个变量有单独的权重，相当于为模型引入了非线性，能够提升模型表达能力，加大拟合；4. 离散化后可以进行特征交叉，由M+N个变量变为M*N个变量，进一步引入非线性，提升表达能力；5. 特征离散化后，模型会更稳定，比如如果对用户年龄离散化，20-30作为一个区间，不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反，所以怎么划分区间是门学问；6. 特征离散化以后，起到了简化了逻辑回归模型的作用，降低了模型过拟合的风险。李沐曾经说过：模型是使用离散特征还是连续特征，其实是一个“海量离散特征+简单模型” 同 “少量连续特征+复杂模型”的权衡。既可以离散化用线性模型，也可以用连续特征加深度学习。就看是喜欢折腾特征还是折腾模型了。通常来说，前者容易，而且可以n个人一起并行做，有成功经验；后者目前看很赞，能走多远还须拭目以待。

4、简单介绍一下逻辑回归
参考博客
关于逻辑回归的几个问题

1. LR原理
2. LR的求解数学推导
3. LR的正则化
4. 为什么LR能比线性回归好？
5. LR与MaxEnt的关系
6. 并行化的LR

这边需要记住的几个重点公式
首先是损失函数，逻辑回归的损失函数是似然函数

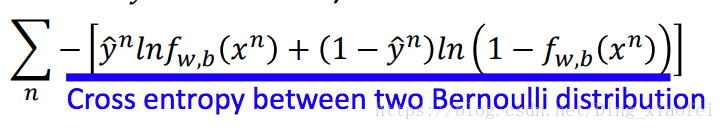
简单地解释一下这个损失函数，原始的似然函数是连成的，每一项就是

记住两个重要的求导公式，也就是我们sigmoid函数的求导公式

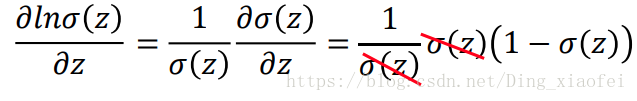
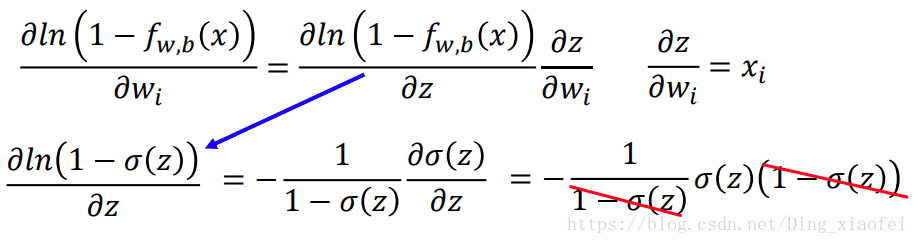
关于逻辑回归和线性回归的损失函数的推导还需要重新推导一下。

5、LR和SVM的联系和区别
参考博客

最后

以上就是饱满保温杯为你收集整理的机器学习面试题解（1-5）的全部内容，希望文章能够帮你解决机器学习面试题解（1-5）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。