常见的机器学习面试题及解答(一)

74 阅读 0 评论 49 点赞

我是靠谱客的博主潇洒书本，最近开发中收集的这篇文章主要介绍常见的机器学习面试题及解答(一)，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1. 线性回归分析中，目标是残差最小化。残差平方和是关于参数的函数，为了求残差极小值，令残差关于参数的偏导数为零，会得到残差和为零，即残差均值为零。

2. m 个元集到n 个元集的映射为n^m个.

3. m 个元集到n 个元集的单射为：当 m=n 时,为 A(m,m)=m! (个) 当 m≠n 时,为0个.

4. m 个元集到n 个元集的满射为：当mn时,情况复杂,需分类讨论 : m=n+1时,为C(m,2)A(n,n)=m(m-1)n!/2(个)

5. 对于一般情况X1+X2+X3+……+Xn=m 的正整数解有 (m-1)C(n-1)
它的非负整数解有 (m+n-1)C(n-1)种

6. 某个神经元输出结果是-0.01，可能使用 Tanh 激活函数
在这里插入图片描述

7. 用梯度下降有参数被训练成为NaN,可能的原因有：

1). 梯度爆炸
2). 计算过程中，出现了被除数为0的情况
3). 学习率或者batchsize设置的太大。因为logits输出太大变成INF，对这个取log就会在求梯度就会变成nan，nan是not a number 的缩写，表示不是一个有理数。所以除了调小学习率这个解决方案，另一个解决方案还可以给loss加正则化项。
4). cost函数中忘记在log的参数中加上一个极小值。
5). 数据中有错误，数据本身就含有了nan的数据，错误的数据导致网络无法收敛。

8. 请你介绍一下，SVM中什么时候用线性核什么时候用高斯核?

当数据的特征提取的较好,所包含的信息量足够大,很多问题是线性可分的那么可以采用线性核。若特征数较少,样本数适中,对于时间不敏感,遇到的问题是线性不可分的时候可以使用高斯核来达到更好的效果。

9. 给你一些数据集，如何进行分类?

提示： 从数据的大小，特征，是否有缺失角度

答：根据数据类型选择不同的模型，如LR或者SVM，决策树。假如特征维数较多，可以选择SVM模型，如果样本数量较大可以选择LR模型，但是LR模型需要进行数据预处理；假如缺失值较多可以选择决策树。选定完模型后，相应的目标函数就确定了。

10. 请你介绍一下矩阵正定性是如何判断的,以及Hessian矩阵正定性在梯度下降中的应用

10.1 矩阵正定性的判断

判断一个矩阵是否正定，可以看此矩阵的所有特征值是否不小于0，如果满足条件，则判定为半正定，若所有特征值都大于0，则判定为正定。

10.2 Hessian矩阵正定性在GD中的应用

在判断优化算法可行性时Hessian 矩阵的正定性起很大的作用。若Hessian 矩阵正定，则函数的2阶偏导恒大于0，函数的变化率处于递增状态，在牛顿法等GD方法中，Hessian 矩阵很容易判断函数是否可收敛到局部或全局最优。

11. 请你简要描述一下k-means算法的流程

(1) 为每个聚类选择一个初始聚类中心
(2) 将样本集按照最小距离原则分配到最邻近聚类
(3) 使用每个聚类的样本均值更新聚类中心
(4) 重复步骤(2)、(3)直到聚类中心不再发生变化
(5) 输出最终的聚类中心和k个簇划分

k-means算法有两个输入参数需要用户指定，一个是簇的个数，另一个是循环次数

K-Means算法知识点

12. 请你简要介绍一下，分层抽样的适用范围是什么

分层抽样利用事先掌握的信息,充分考虑了保持样本结构和总体结构的一致性,当总体由差异明显的几部分组成的时候,适合用分层抽样。

13. 请你谈一谈word2vec、glove和 fasttext 各自的特点和优势

(1). Word2vec

处理文本任务首先要将文字转换成计算机可处理的数学语言，比如向量，Word2vec就是用来将一个个的词变成词向量的工具。word2vec包含两种结构，一种是skip-gram结构，一种是cbow结构，skip-gram结构是利用中间词预测邻近词，cbow模型是利用上下文词预测中间词。

(2). fasttext

fastText简单来说就是将句子中的每个词先通过一个 lookup 层映射成词向量，然后对词向量取平均作为整个句子的句子向量，然后直接用线性分类器进行分类，从而实现文本分类。不同于其他的文本分类方法的地方在于，这个fastText完全是线性的，没有非线性隐藏层，得到的结果和有非线性层的网络差不多，这说明对句子结构比较简单的文本分类任务来说，线性的网络结构完全可以胜任，而线性结构相比于非线性结构的优势在于结构简单，训练的更快。

这是对于句子结构简单的文本来说，但是这种方法显然没有考虑词序信息，对于那些对词序很敏感的句子分类任务来说（比如情感分类）fastText就不如有隐藏层等非线性结构的网络效果好。

fastText是一个文本分类算法，是一个有监督模型，有额外标注的标签CBOW是一个训练词向量的算法，是一个无监督模型，没有额外的标签，其标准是语料本身，无需额外标注。用fastText做文本分类的关键点是极大地提高了训练速度（在要分类的文本类别很多的情况下，比如500类），原因是在输出层采用了层级softmax。

(3). glove

glove也在word2vec上面进行了改进，利用平方损失来替代了交叉熵损失，一个是交叉熵损失计算中的规范化概率依赖于词在分母中的累加项，会带来很大的计算开销，另外一方面生僻词在词典中出现的概率往往很少，所以生僻字的条件概率分布在交叉熵损失中最终的预测往往不够准确。

fastText原理和文本分类实战
word2vec、glove和 fasttext 的比较

14. 请你讲一下，关于监督学习和无监督学习，最大的区别是什么？

根据训练数据是否有标签，学习任务可大致划分为“监督学习”和“无监督学习”。

监督学习方法必须要有训练集与测试样本。利用训练数据集学习一个模型，再用模型对测试样本集进行预测。

无监督学习没有训练集，只有一组数据，在该组数据集内寻找规律。试图使簇内差距最小化，簇间差距最大化。

其中，分类和回归是监督学习的代表，而聚类则是无监督学习的代表。

15. 请你简要描述一下什么是支持向量机,以及SVM与LR的区别?

支持向量机就是尝试找到一个最能够区分数据集的超平面对数据进行分类。

对于LR来说，所得的结果是该数据点的分类概率(0到1之间)

而SVM则是尝试找到一个离两边数据点最远的超平面

相同点：

LR和SVM都是线性分类器。
如果不考虑核函数，LR和SVM都是线性分类算法，即分类决策面都是线性的。
LR和SVM都是监督学习算法。

不同点

损失函数不同，LR是对数损失log loss，SVM是合页损失hinge loss。
LR受所有数据影响，而SVM只考虑局部的边界线附近的点（支持向量）。

支持向量机SVM中常见的面试问题QA

16. 请你简要介绍一下SVM的作用以及基本实现原理

(1). SVM的作用

SVM可以用于解决二分类或者多分类问题，此处以二分类为例。SVM的目标是寻找一个最优化超平面在空间中分割两类数据，这个最优化超平面需要满足的条件是：离其最近的点到其的距离最大化，这些点被称为支持向量。

(2). 基本实现原理

最大间隔原则
对偶表示
KKT条件

[1]. 机器学习笔记6：SVM基本原理
[2]. SVM算法原理与实现

17. 请问如何求m*k矩阵A和n*k矩阵的欧几里得距离?

在做分类时，常常需要估算两个样本间的相似性度量(SimilarityMeasurement)，这时经常就用到两个样本间的"距离"，常用的度量方法是欧式距离

在使用k-NN模型时，需要计算测试集中每一点到训练集中每一点的欧氏距离，即需要求得两矩阵之间的欧氏距离。在实现k-NN算法时通常有三种方案，分别是使用两层循环，使用一层循环和不使用循环。

(1). 使用两层循环

分别对训练集和测试集中的数据进行循环遍历，计算每两个点之间的欧式距离，然后赋值给dist矩阵。此算法没有经过任何优化。

num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in range(num_test):
  for j in range(num_train):
    dists[i][j] = np.sqrt(np.sum(np.square(X[i] - self.X_train[j])))
      
return dists

(2). 使用一层循环

使用矩阵表示训练集的数据，计算测试集中每一点到训练集矩阵的距离，可以对算法优化为只使用一层循环。(分解为点到矩阵之间的距离)

def compute_distances_one_loop(self, X):
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train))
    for i in range(num_test):
      dists[i] = np.sqrt(np.sum(np.square(self.X_train - X[i]), axis = 1))
    return dists

(3). 不使用循环

运算效率最高的算法是将训练集和测试集都使用矩阵表示，然后使用矩阵运算的方法替代之前的循环操作。但此操作需要我们对矩阵的运算规则非常熟悉。接下来着重记录如何计算两个矩阵之间的欧式距离。

记录测试集矩阵P的大小为M*D，训练集矩阵C的大小为N*D（测试集中共有M个点，每个点为D维特征向量。训练集中共有N个点，每个点为D维特征向量）

记 $P_i$ 是 $P$ 的第 $i$ 行，记 $C_j$ 是 $C$ 的第 $j$ 行

$P_{i}=left[begin{array}{ccc}P_{i 1} & P_{i 2} cdots P_{i D}end{array}right] quad C_{j}=left[begin{array}{cc}C_{j 1} C_{j 2} cdots & C_{j D}end{array}right]$

首先计算 $P_i$ 和 $C_j$ j之间的距离 $d i s t (i, j)$

$dleft(P_{i}, C_{j}right)=sqrt{left(P_{i 1}-C_{j 1}right)^{2}+left(P_{i 2}-C_{j 2}right)^{2}+cdots+left(P_{i D}-C_{j D}right)^{2}}$
$=sqrt{left(P_{i 1}^{2}+P_{i 2}^{2}+cdots+P_{i D}^{2}right)+left(C_{j 1}^{2}+C_{j 2}^{2}+cdots+C_{j D}^{2}right)-2}$
$sqrt{timesleft(P_{i 1} C_{j 1}+P_{i 2} C_{j 2}+cdots+P_{i D} C_{i D}right)}$
$=sqrt{left|P_{i}right|^{2}+left|C_{j}right|^{2}-2 times P_{i} C_{j}^{T}}$

我们可以推广到距离矩阵的第 $i$ 行的计算公式

$dist_[i] =sqrt{(left|P_{i}right|^{2} left|P_{i}right|^{2}...left|P_{i}right|^{2})+(left|C_{1}right|^{2}left|C_{2}right|^{2}...left|C_{n}right|^{2})-2 times P_{i} (C_{1}^{T}C_{2}^{T}...C_{n}^{T})}$
$=sqrt{(left|P_{i}right|^{2} left|P_{i}right|^{2}...left|P_{i}right|^{2})+(left|C_{1}right|^{2}left|C_{2}right|^{2}...left|C_{n}right|^{2})-2 times P_{i} C^{T}}$

继续将公式推广为整个距离矩阵
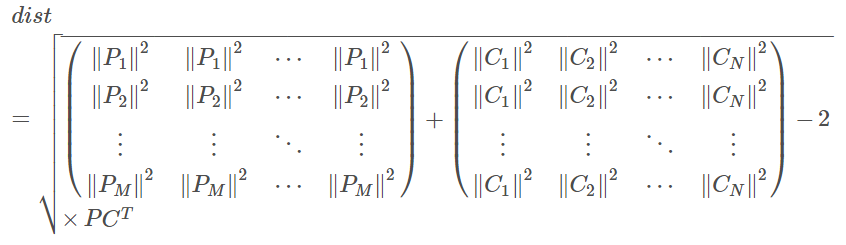
在这里插入图片描述

def compute_distances_no_loops(self, X):
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train)) 
    dists = np.sqrt(-2*np.dot(X, self.X_train.T) + np.sum(np.square(self.X_train), axis = 1) + np.transpose([np.sum(np.square(X), axis = 1)]))
    return dists

计算两个矩阵之间的欧式距离

18. 请你解释一下SVM使用对偶计算的目的是什么，是如何推出来的

目的有两个：一是方便核函数的引入；二是原问题的求解复杂度与特征的维数相关，而转成对偶问题后只与问题的变量个数有关。由于SVM的变量个数为支持向量的个数，相较于特征位数较少，因此转对偶问题。
通过拉格朗日算子使带约束的优化目标转为不带约束的优化函数，使得W和b的偏导数等于零，带入原来的式子，再通过转成对偶问题。

https://www.nowcoder.com/interview/ai/report?roomId=173043

19. 请你简要描述一下LR和线性回归的区别

(1). 区别：

区别	线性回归（liner regression）	LR（logistics regression）
构建方法	最小二乘法	似然函数
解决问题	主要解决回归问题，也可以用来分类，但是鲁棒性差。	解决分类问题
输出	输出实数域上连续值	LR通过Sigmod函数将实数域映射到 [0，1]

(2). 联系：

线性回归和LR都是广义上的线性回归，都是通过一系列输入特征拟合一条曲线来完成未知输入的预测。

LR和线性回归的区别与联系

20. 请你简要讲一下对于改进模型的两种方法AdaBoost和GBDT的区别