全栈工程师开发手册 (作者:栾鹏)
python数据挖掘系列教程
回归评估指标
均方误差(MSE)
MSE (Mean Squared Error)叫做均方误差。看公式
1
m
∑
i
=
1
m
(
y
i
−
f
(
x
i
)
)
2
frac{1}{m}sum_{i=1}^m(y_i-f(x_i))^2
m1i=1∑m(yi−f(xi))2
均方根误差(RMSE)
RMSE(Root Mean Squard Error)均方根误差。
1
m
∑
i
=
1
m
(
y
i
−
f
(
x
i
)
)
2
sqrt{frac{1}{m}sum_{i=1}^m(y_i-f(x_i))^2}
m1i=1∑m(yi−f(xi))2
这是MSE开个根号,其实实质是一样的。只不过用于数据更好的描述。
MAE
MAE(平均绝对误差)
1 m ∑ i = 1 m ∣ y i − f ( x i ) ∣ frac{1}{m}sum_{i=1}^m|y_i-f(x_i)| m1i=1∑m∣yi−f(xi)∣
分类评估
1.1、 混淆矩阵
混淆矩阵用在分类器中,是对每一类样本的统计,包括正确分类和错误分类的个数。对于m类样本,可能的错误种类有 m 2 − m m^2−m m2−m个。
用正元组P(Positive)表示我们感兴趣的分类。
用负元素N(Negative)表示我们不感兴趣的分类
用True表示样本被正确分类
用False表示样本被错误分类。
则
FN:False Negative,被错误判定为负样本,但事实上是正样本。
FP:False Positive,被错误判定为正样本,但事实上是负样本。
TN:True Negative,被正确判定为负样本,事实上也是负样本。
TP:True Positive,被正确判定为正样本,事实上也是正样本。
1.2、 准确率及误差率的度量
| 度量 | 公式 | 描述 |
|---|---|---|
| 准确率、识别率 | T P + T N P + N frac{TP+TN}{P+N} P+NTP+TN | 正确分类的样本数与检测样本总数的比值 |
| 错误率、误分类率 | F P + F N P + N frac{FP+FN}{P+N} P+NFP+FN | 错误分类的样本数与检测样本总数的比值 |
| 敏感度、真正例率、召回率 | T P P frac{TP}{P} PTP | 正元组中被准确预测的比例 |
| 特效率、真负例率 | T N N frac{TN}{N} NTN | 负元组中被准确预测的比例 |
| 错误正例、假正率 | F N F N + T N frac{FN}{FN+TN} FN+TNFN | 正元组被预测成负元组的样本数占预测结果为负元组样本数的比例 |
| 错误负例、假负率 | F P F P + T P frac{FP}{FP+TP} FP+TPFP | 负元组被错误当成正元组的样本数占预测结果为正元组样本数的比例 |
| 精度 | T P T P + F P frac{TP}{TP+FP} TP+FPTP | 在预测结果的正元组的集合里真实正元组的比例 |
| F、 F 1 F_1 F1、F分数精度和召回率的调和均值 | 2 ∗ 精 度 ∗ 召 回 率 精 度 + 召 回 率 frac{2*精度*召回率}{精度+召回率} 精度+召回率2∗精度∗召回率 | |
| F β F_β Fβ | ( 1 + β 2 ) ∗ 精 度 ∗ 召 回 率 β 2 ∗ 精 度 + 召 回 率 frac{(1+β^2)*精度*召回率}{β^2∗精度+召回率} β2∗精度+召回率(1+β2)∗精度∗召回率 | β=1退化为 F 1 F_1 F1;β>1召回率有更大影响;β<1精度有更大影响。 |
宏平均(macro-average):一般用在文本分类器,是先对每一个类统计指标值,然后在对所有类求算术平均值。宏平均指标相对微平均指标而言受小类别的影响更大。
微平均(micro-average):一般用在文本分类器,是对数据集中的每一个实例不分类别进行统计建立全局混淆矩阵,然后计算相应指标。
**平均准确率(Average Per-class Accuracy)????*为了应对每个类别下样本的个数不一样的情况,计算每个类别下的准确率,然后再计算它们的平均值。
**对数损失函数(Log-loss)????*在分类输出中,若输出不再是0-1,而是实数值,即属于每个类别的概率,那么可以使用Log-loss对分类结果进行评价。这个输出概率表示该记录所属的其对应的类别的置信度。比如如果样本本属于类别0,但是分类器则输出其属于类别1的概率为0.51,那么这种情况认为分类器出错了。该概率接近了分类器的分类的边界概率0.5。Log-loss是一个软的分类准确率度量方法,使用概率来表示其所属的类别的置信度。
1.3、 评价模型成本的可视化工具
1.3.1、 lift图
lift叫提升指数,也就是运用模型比不运用模型精度的提升倍数。
$lift=frac{TP}{TP+FP} /frac{TP+FN}{P+N} $
也可以表示为
$lift=frac{累计预测精度}{平均精度} $
结论是:lift提升指数越高,模型的准确率越高。
用在数据挖掘模型里也是一样,利用模型能对准确率提升越多,单方面来讲模型效果就越好。
1.3.2、ROC曲线
ROC曲线是利用真正率(正元组中被准确预测的比例)为纵轴,假正率(预测结果为负元组的样本中实际为正元组的比例)为横轴画出的曲线,用来评估模型预测准确率。很明显,当真正率大越近1,假正率越接近0是模型越好。
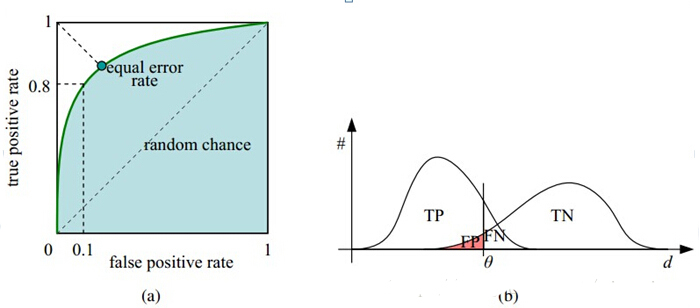
对于给定的一组样本,我们只能得到一个真正率和一个假正率(对应图上的一个点),那如何画ROC曲线呢?
通过设置不同的阈值,比如逻辑回归中可以设定概率>0.5的点为正例,在此阈值下可以得到ROC曲线上的一个点;更改阈值,如概率>0.6的点为正例,同样可以得到ROC曲线上的一个点;不同的阈值可以得到一组点,即得到了ROC曲线;
真正率大越近1,假正率越接近0是模型越好,在图上的表现就是ROC曲线越靠近(0,1)点,越远离45o对角线;
为什么要使用ROC曲线呢?
因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变换的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现样本类不平衡,即正负样本比例差距较大,而且测试数据中的正负样本也可能随着时间变化。
1.3.3、AUC
AUC(area under curve):即ROC曲线下的面积。
若一个学习器的ROC曲线被另一个包住,后者的性能能优于前者;若交叉,判断ROC曲线下的面积,即AUC。
下面给出AUC的一个计算方法。
假设有m+n个样本,其中m个正样本,n个负样本。
模型对(m+n)个样本进行概率预测,得到的每个样本属于正样本的概率,并对这些样本的概率值由大到小进行排序。为
p
1
,
p
2
,
p
3
.
.
.
.
p
m
+
n
p_1,p_2,p_3....p_{m+n}
p1,p2,p3....pm+n
那么我们从样本随意取两个样本的预测概率 p i , p j p_i,p_j pi,pj,其中 p i > p j p_i>p_j pi>pj,如果样本i为正样本,样本j为负样本,则这种组合为正面组合。
a u c = 所 有 正 面 组 合 数 m ∗ n auc=frac{所有正面组合数}{m*n} auc=m∗n所有正面组合数
分母好理解,就是真实情况下,正负样本的组合数目。分子为正类样本的score大于负类样本的score的所有组合数目。
关于所有正面组合数的计算可以通过:
首先对score从大到小排序,然后令最大score对应的sample 的rank为n,第二大score对应sample的rank为n-1,以此类推。然后把所有的正类样本的rank相加,再减去M-1种两个正样本组合的情况。得到的就是所有的样本中有多少对正类样本的score大于负类样本的score
所以
A U C = ∑ 正 样 本 r a n k i − M ( M + 1 ) 2 M ∗ N AUC=frac{sum_{正样本}rank_i-frac{M(M+1)}{2}}{M*N} AUC=M∗N∑正样本ranki−2M(M+1)
也就是说,如果模型预测的概率,所有正样本的预测概率都比所有负样本的预测概率大,则auc输出为1。
也就是说auc评估的是样本概率的排序能力。
1.4、 评估分类器的准确率
上面讲的评价模型的指标或曲线都是在测试集中进行的,也就是我们需要将数据集分为训练集和测试集,训练集用于训练模型参数,测试集用于检验模型在数据中的预测效果。这就是我们评估分类器大的方法。下面介绍将数据划分为训练集和测试集的方法。
1.4.1、 再替换方法
所有的数据即用于训练模型也用于检验模型
1.4.2、 保持方法和随机子抽样
保持方法(hold out):按一定比例随机地从数据集中抽取一部分样本作训练集,剩下的样本为测试集,通长训练集在 2 3 frac{2}{3} 32~ 4 5 frac{4}{5} 54之间;
随机子抽样(random subsampling):抽取一定比例样本做为训练集,剩下的样本为测试集;然后在第1次的训练集重复该操作;重复n次,评论指标的平均值作为最终的评价值;这是一种无放回抽样;
1.4.3、 交叉验证法
K折交叉验证(K-fold cross-validation):将样本分成K份,每份数量大致相等,然后用其中的某一份作为测试,其他样本作为训练集,得到一个模型和一组预测值及模型评估值;循环这个过程K次,得到K组模型评估值,对其取平均值即得到最终的评估结果;
留一(leave-one-out):是K-fold cross-validation的特征形式,每次只取一个样本作为测试样本,其余样本作为训练样本,重复该过程K次(假如样本总数为K)。
1.4.4、 自助法
自助法(bootstrap method):在数据集中采用有放回的方式抽样,产生训练集和测试集;重复该过程n次。
2、 基于统计检验的标准
2.1、 统计模型之间的距离
距离是典型的相似性指标。
欧氏距离
熵距离
卡方距离
0-1距离
我并不认为用距离评估模型的效果是一种好的做法,只有不同类样本在样本内扎堆,类间分离的时候这种检测才是一致的。
2.2、 统计模型的离差
离差即误差的统称:如标准差,方差都为这一类
欧氏离差即为平均误差和。
3、 基于记分函数的标准
4、 贝叶斯标准
5、计算标准
5.1、 交叉检验(CV)标准
交叉验证(Cross Validation)是用来验证分类器的性能一种统计分析方法,基本思想是把在某种意义下将原始数据(dataset)进行分组,一部分做为训练集 (training set),另一部分做为验证集(validation set),首先用训练集对分类器进行训练,在利用验证集来测试训练得到的模型(model),以此来做为评价分类器的性能指标。常见的交叉验证方法如下:
1、Hold-Out Method
将原始数据随机分为两组,一组做为训练集,一组做为验证集,利用训练集训练分类器,然后利用验证集验证模型,记录最后的分类准确率为此分类器的性能指标。 此种方法的好处的处理简单,只需随机把原始数据分为两组即可,其实严格意义来说Hold-Out Method并不能算是CV,因为这种方法没有达到交叉的思想,由于是随机的将原始数据分组,所以最后验证集分类准确率的高低与原始数据的分组有很大的关 系,所以这种方法得到的结果其实并不具有说服性。
2、Double Cross Validation(2-fold Cross Validation,记为2-CV)
做法是将数据集分成两个相等大小的子集,进行两回合的分类器训练。在第一回合中,一个子集作为训练集,另一个便作为测试机;在第二回合中,则将训练集与测试集对换后,再次训练分类器,而其中我们比较关心的是两次测试集的辨识率。不过在实务上2-CV并不常用,主要原因是训练集样本数太少,通常不足以代表母体样本的分布,导致测试阶段辨识率容易出现明显落差。此外,2-CV中分子集的变异度大,往往无法达到“实验过程必须可以被复制”的要求。
3、K-fold Cross Validation(K-折交叉验证,记为K-CV,也叫S折交叉验证)
将原始数据分成K组(一般是均分),将每个子集数据分别做一次测试集,其余的K-1组子集数据作为训练集,这样会得到K个模型,用这K个模型最终的测试集的分类准确率的平均数作为此K-CV下分类器的性能指标。K一般大于等于2,实际操作时一般从3开始取,只有在原始数据集合数据量小的时候才会尝试取 2。K-CV可以有效的避免过学习以及欠学习状态的发生,最后得到的结果也比较具有说服性。如果作为模型选择,最后选出K次评测中测试误差最小的模型。
4、Leave-One-Out Cross Validation(记为LOO-CV,也叫做留一交叉验证)
如果设原始数据有N个样本,那么LOO-CV就是N-CV,即每个样本单独作为测试集,其余的N-1个样本作为训练集,所以LOO-CV会得到N个模型测试集的分类准确率的平均数作为此下LOO-CV分类器的性能指标。相比于前面的K-CV,LOO-CV有两个明显的优点:
(1)每一回合中几乎所有的样本皆用于训练模型,因此最接近原始样本的分布,这样评估所得的结果比较可靠。
(2)实验过程中没有随机因素会影响实验数据,确保实验过程是可以被复制的。
但LOO-CV的缺点则是计算成本高,因为需要建立的模型数量与原始数据样本数量相同,当原始数据样本数量相当多时,LOO-CV在实作上便有困难几乎就是不显示,除非每次训练分类器得到模型的速度很快,或是可以用并行化计算减少计算所需的时间。
5.2、 自展标准
5.3、 遗传算法
6、其他评价指标
计算速度:分类器训练和预测需要的时间;
鲁棒性:处理缺失值和异常值的能力;
可扩展性:处理大数据集的能力;
可解释性:分类器的预测标准的可理解性,像决策树产生的规则就是很容易理解的,而神经网络的一堆参数就不好理解,我们只好把它看成一个黑盒子。
7、回归模型评估指标
RMSE(root mean square error,平方根误差):其又被称为RMSD(root mean square deviation),RMSE对异常点(outliers)较敏感,如果回归器对某个点的回归值很不理性,那么它的误差则较大,从而会对RMSE的值有较大影响,即平均值是非鲁棒的。其定义如下:
Quantiles of Errors: 为了改进RMSE的缺点,提高评价指标的鲁棒性,使用误差的分位数来代替,如中位数来代替平均数。假设100个数,最大的数再怎么改变,中位数也不会变,因此其对异常点具有鲁棒性。
聚类模型评估
1.1 Adjusted Rand index 调整兰德系数

1.2 Mutual Information based scores 互信息

1.3 Homogeneity, completeness and V-measure
同质性homogeneity:每个群集只包含单个类的成员。
完整性completeness:给定类的所有成员都分配给同一个群集。
两者的调和平均V-measure。
1.4 Fowlkes-Mallows scores

1.5 Silhouette Coefficient 轮廓系数

1.6 Calinski-Harabaz Index
这个计算简单直接,得到的Calinski-Harabasz分数值ss越大则聚类效果越好。Calinski-Harabasz分数值ss的数学计算公式是:

也就是说,类别内部数据的协方差越小越好,类别之间的协方差越大越好,这样的Calinski-Harabasz分数会高。
在scikit-learn中, Calinski-Harabasz Index对应的方法是metrics.calinski_harabaz_score.
在真实的分群label不知道的情况下,可以作为评估模型的一个指标。
同时,数值越小可以理解为:组间协方差很小,组与组之间界限不明显。
与轮廓系数的对比,笔者觉得最大的优势:快!相差几百倍!毫秒级
最后
以上就是明亮鲜花最近收集整理的关于python机器学习案例系列教程——模型评估总结的全部内容,更多相关python机器学习案例系列教程——模型评估总结内容请搜索靠谱客的其他文章。








发表评论 取消回复