FCOS目标检测论文各种细节解读

83 阅读 0 评论 55 点赞

我是靠谱客的博主长情小海豚，最近开发中收集的这篇文章主要介绍FCOS目标检测论文各种细节解读，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

写在博客的最最最前面，我不得不说，本来我是不想写FCOS的，因为确实网上很多博客都有在讲，而且论文整体据说比较好理解，但是我发现我看了很多篇博客都一模一样，而且吧，他们还不讲细节，就比如为啥引入FPN之后模糊样本就少了？为什么引入 $s_{i}$ （详细见章节7）？还有就是他们一直在说FCOS共享了head，论文原文证据（原文也只说了共享head）和代码都没有。。。然后你看FCOS论文的模型图你可能还想象不到P3~P7用的是同一个head，只不过 $s_{i}$ 不一样。对于“神”来说，可能一点就通，但我是凡人啊！所以啊，我是真的没办法。。只能看看代码，看看论文写了这篇博客。愁人。。。零零散散用时1周，如果这篇博客有什么不对，请你们一定指出来，我们一起讨论下！还有这篇博客有什么没讲到你想知道的评论区见吧，因为我写博客本来就奔着细节去的，那种大体一看就懂的一般不会写。

FCOS（Fully Convolutional One-Stage Object Detection ）

论文地址：https://arxiv.org/abs/1904.01355 代码地址：https://github.com/tianzhi0549/FCOS/

1. Anchor-based 方法的缺点

2. FCOS模型结构

3. 论文中一些比较重要的定义

4. FPN结构及作用

5. Center-ness layer

6. 损失函数

7. 补充一些细节

8. 实验结果与个人的一点心得

先要明确的知道，FCOS是一个基于FCN（全卷积网络用于目标检测）、一阶段（one stage）、anchor free、proposal free、参考语义分割思想实现的逐像素目标检测的模型。

简要介绍下FCOS几个核心点：

（1）FCOS方法借鉴了FCN的思想，对 feature map 上每个特征点做回归操作，预测四个值 $(l, r, t, d)$ ，分别代表特征点到Ground Truth Bounding box上、下、左、右边界的距离。

（2）特征点映射会原图后对应多个GT Bounding box，无法准确判断原图像素所属类别，因此模型引入 FPN 结构，利用不同的层来处理不同尺寸的目标框。

（3）远离目标中心点可能会产生劣质预测结果，为了增强中心点选取的准确性，模型引入了Center-ness layer。

（4）损失函数由三个部分构成：分类损失focal loss；回归损失iou loss；center-ness损失 BCE。

1. Anchor-based 方法的缺点

在前些时候主流的目标检测论文研究大多都是anchor-base，我们熟知的就有SSD、YOLOV2、YOLOV3、Faster-R-CNN、Mask-R-CNN（啥都能做。。），而且准确率最高的大多都是这类anchor-base的模型。

但是anchor-base也有不少缺陷：

anchor-base模型的检测性能一定程度上依赖于anchor的设计，anchor的基础尺寸、长宽比、以及每一个特征点对应的anchor数目等。比如Faster提出的基准anchor大小16，3种倍数[8, 16, 32] 以及三种比例，共9种anchor。
设定好anchor了只能说是匹配到大部分目标，对于那些形变较大的目标检测起来还是比较困难，尤其是小目标（小目标识别已经是一个研究方向了）。同时这也一定程度上限制了模型的泛化能力。
为了取得较好的召回率（将负例识别为正例的概率越小，Recall越大），那就需要为每个特征点安排更密集的anchor，假如我们为了性能同时考虑形如FPN这样的多尺度结构，在前向推演以及NMS等操作时，显存以及CPU消耗很大。
在这些放置的更密集的anchor中，大多数anchor属于负样本，这样也造成了正负样本之间的不均衡。（Faster好像各选128 positive / negtive 作为训练anchor，不过肯定不是随机挑选的）。

这里讲一些我在实际论文和项目中的感觉啊，基于anchor-base的模型就单说准确率来说已经很高了，但是相对的FPS会低一些，可是！！现实中的项目包括各种制造厂、车载设备、道路设备最终都是需要集成到板端的，现在你搞了密集anchor，在前向推演以及NMS等操作耗时太长，必然不能满足需求。从研究论文角度来讲，anchor-base的门槛已经很高了。。所以大家都开始转战anchor-free，而且还取得了不错的成效，有些想法很棒。

2. FCOS模型结构

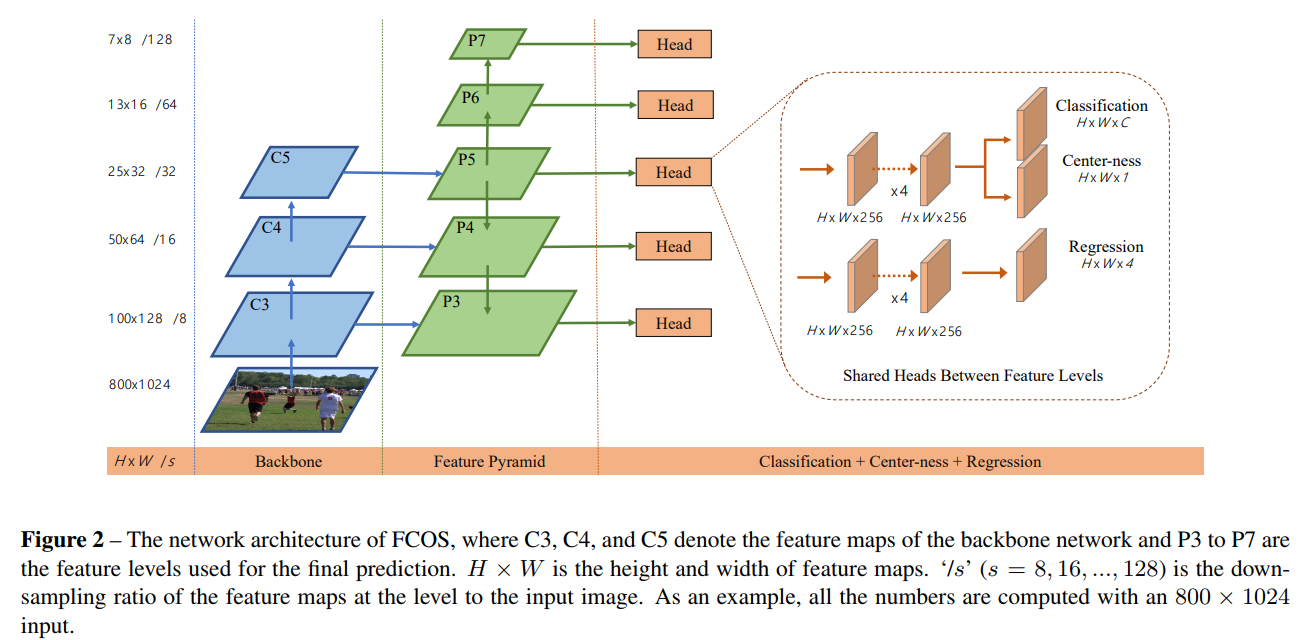
上图就是FCOS的模型结构图，可以看到整体还是很传统的Backbone + Feature Pyramid Net + head (包括分类分支、center-ness分支、回归分支（回归预测距离）)。

3. 论文中一些比较重要的定义

（1）第 i 个 GT Bounding box定义为： $B_{i} = ({x_{0}}^{(i)}, {y_{0}}^{(i)}, {x_{1}}^{(i)}, {y_{1}}^{(i)}}, c^{(i)}})$ ，其中 $({x_{0}}^{(i)}, {y_{0}}^{(i)})$ ， $({x_{1}}^{(i)}, {y_{1}}^{(i)})$ 表示当前Bounding box 左上角以及右下角的坐标。

（2）模型回归分支预测的是当前点 $(x, y)$ 到GT Bounding box边界的距离 $(l, r, t, d)$ ，在计算损失函数时候与之对应的真实标签定义为： $(l^{*}, r^{*}, t^{*}, d^{*})$ ，值如下计算：

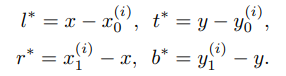
（3）每一个feature map上的特征点都是一个样本，但是在回归之前要映射回原图进行正负样本的判断，映射回原图后的点如果在某一个GT Bounding box内，则对应的特征点是正样本，类别就是Bounding box内目标的类别；否则，负样本。

（4）将feature map上的特征点映射回原图：需要按照 s（下采样总倍数，因为用了FPN，每一个特征图下采样倍数不一样）将特征点映射回原图，现在假定特征图上点 $(x, y)$ ，对应原图位置 $(x^{'}, y^{'})$ ，其中 $(x^{'}, y^{'}) = (floor(frac{s}{2}) + xs, floor(frac{s}{2}) + ys)$ ，floor表示下取整。

4. FPN结构及作用

本文将 feature map 上每一个特征点作为样本，当 $(x^{'}, y^{'})$ 落在多个GT Bounding box内，论文称这样的特征点为 "模糊样本"（ambiguous sample），那么模糊样本应该回归的边界框对应哪个GT Bounding box？

本文是这样抉择的：（1）引入FPN结构实现多级预测（2）在多级预测筛选后如果某一个特征点还是匹配多个GT Bounding box，这种情况简单的选择面积更小的GT Bounding box作为该特征点的回归目标。

当然模糊样本的出现，还是会干扰当前像素属于哪一类的判断。

If a location falls into multiple bounding boxes, it is considered as an ambiguous sample. We simply choose the bounding box with minimal area as its regression target.

本文通过多层级feature map的预测（引入FPN，{P3，P4，P5，P6，P7}）来解决模糊样本的问题，说实话这一块其实不是很好懂，我最开始就很疑惑引入了多层级feature map，再把每一级feature map的特征点映射回原图，最后回归岂不是增加了冲突的次数以及计算量？

但是后来仔细看了论文以及查看了很多博客之后，发现FCOS其实是使用不同层级的 feature map 检测不同尺寸的目标（如果是anchor-base的话，这一块难道不就是不同层级的feature map设置不同大小的anchor尺寸吗？），为了实现这样的需求就需要引入一个阈值，该阈值限制不同层级特征回归预测一定范围内尺寸的目标。

Following FPN [14], we detect different sizes of objects on different levels of feature maps.

不同于anchor-base的模型，在不同层级的 feature map上应用不同尺寸的anchor，FCOS选择设置阈值限制每一层feature map的回归范围。具体操作：首先计算出不同层级feature map上每个特征点对应的回归目标 $(l^{*}, r^{*}, t^{*}, d^{*})$ （距离是基于原图计算的），

如果特征点满足 ${color{Red} max(l^{*}, r^{*}, t^{*}, d^{*}) > m_{i}}$ 或者 ${color{Red} max(l^{*}, r^{*}, t^{*}, d^{*}) < m_{i-1}}$ ，则将特征点认定为负样本，没有回归的意义，其中 $m_{i}$ 表示第 i 层 feature map 需要回归的最大距离（本文设置 $m_{2}, m_{3}, m_{4}, m_{5}, m_{6}, m_{7} = 0, 64, 128, 256, 512, infty$ ），因为具有不同大小的对象被分配到不同的特征级别，而大多数重叠发生在大小差异较为明显的对象之间。补充一下：P3回归的范围就是[0, 64]，P4回归的范围就是[64, 128]。一定要注意：判定某一层级特征点是正样本还是负样本，本质上是依靠的是特征点映射回原图后的像素点距离所述GT Bounding box边框的真实距离。

Since objects with different sizes are assigned to different feature levels and most overlapping happens between objects with considerably different sizes # 大多数重叠发生在大小差异较为明显的对象之间

补充：看到这里应该还有很多小伙伴不明白为啥FPN就能减少模糊样本了，我也是刚想明白，其实是这样的，以P3举例，P3里面所有的特征点映射回原图后，原图上对应点可能对应很多个GT Bounding box，但是我们现在加了限制，要求这些个点的归属只能是那些距离点小于64像素的Bounding box。

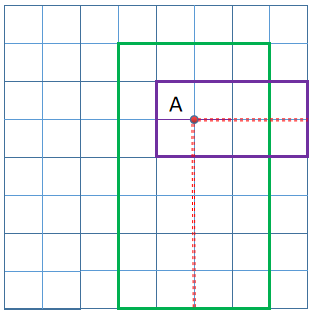
看图，加入P3上的某一个特征点映射回了原图（红色点A），A在两个GT Bounding box里面，这里就分两种情况了：

（1）假定原图（下图）一个格子表示16px，A距离紫色Bounding box边界的最大距离为48（3 * 16）px，A距离绿色Bounding box边界的最大距离为 90（5 * 16）px，那么根据阈值，我们认为A属于紫色Bounding box，回归对应的GT是紫色框；当然如果没有紫色框，那么A将归于负样本，因为没有GT Bounding box收留他（满足 ${color{Red} max(l^{*}, r^{*}, t^{*}, d^{*}) > m_{i}}$ ${color{Red} max(l^{*}, r^{*}, t^{*}, d^{*}) < m_{i-1}}$ 就归于负样本）

（2）如果原图（下图）一个格子表示8px，那么A距离紫色Bounding box边界的最大距离为24px，A距离绿色Bounding box边界的最大距离为40px，此时A距离不同box的最大距离都符合要求（0~64px），那么只能选择面积更小的紫色GT Bounding box作为A的回归目标

5. Center-ness layer

在引入FPN结构实现多层级feature map预测后，在性能方面 FCOS 仍与 anchor-base 的模型存在一定差距。这是由于距离目标中心较远的位置预测出大量低质量的Bounding box造成的，简单点说就是某一个层级的特征点映射到原图上的点位于真实GT Bounding box的边缘或者位于距离box目标中心较远的位置，因此模型在学习和预测的时候可能认为这个点不属于它本该对应的目标，但这样造成的结果就是本该回归目标是某一个GT Bounding box的特征点预测出了一个新的box，而这个box没有特别大的意义（并不完全正确，也可以这么理解，本该归类为某一个目标的特征点错误预测成了其它类）。

解决这个问题，核心在于让模型学习到“中心度”，也可以理解成哪些点才是目标最可能的中心点（反向告诉某些特征点，它不是中心点，预测的box没有特别大的意义，这样就抑制了低质量box的产生）。

原文是这么说的：The center-ness depicts the normalized distance from the location to the center of the object that the location is responsible for

中心度描绘从该位置到该位置负责的目标的真实中心的标准化（量化）距离。

那么现在的问题变成了如何量化/标准化当前点到负责它的目标的中心的距离：

很容易想到目标中心点对应的值应该 = 1，距离中心点越远，对应center-ness的值想当然应该越来越小并趋近于0。并且既然还是“学习”，那就必定有真实值标签（GT），该真实值标签计算方法如下：

当 feature map上的特征点映射回原图后，根据章节4中的判断得到对应的GT Bounding box以及距离该box边界的距离 $(l^{*}, r^{*}, t^{*}, d^{*})$ ，直接计算就能得到该特征点对应的centerness值。

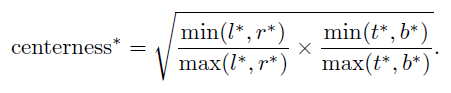
这部分使用BCE损失（二值交叉熵）。

注意：我个人认为这个部分核心作用还是在推理（测试）这个部分，对于FPN网络结构的每一层特征最终输出 3 部分内容：Classification、Regression 和 Center-ness。

模型最终的目的是输出一组置信度高的box和类别，因此后续使用NMS进行筛选，我们知道NMS是需要一组置信度得分的，那么这个置信度得分如何计算那？是的。。就是模型的输出的 Final置信度 = （类别概率）* （对应的center-ness），根据公式我们可以发现 center-ness 可以看做是一个注意力机制（加权），让模型更加关注那些距离真实目标中心点近的预测box，即使距离中心点远的的点类别概率得分很高，因为center-ness的存在也能抑制该点的置信度，仍会被NMS筛除。

6. 损失函数

这部分比较好理解，很传统，根据上上上上网络结构图可知，针对某一个层级的 feature map，head的输出有三个部分：classification（H * W * C）、regression（H * W * 4）、center-ness(H * W * 1)，其中C是类别总数，H * W是特征图尺寸。

先上图和公式：

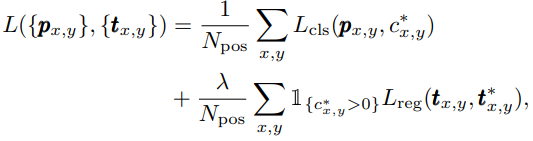
虽然很传统但是还是有所区别：

分类损失：舍弃了softmax，改为对head输出的classification（H * W * C）每一个通道（每一个通道代表一种类别）分别使用sigmoid函数，然后使用 Focal loss。这样做的好处，在我的理解中是为了保留类别之间的关联特性。

回归损失：IOU Loss，仅对那些有意义的特征点进行回归计算。有意义是什么意思那？其实就是先将特征点映射回原图，看看原图上对应的点在不在某一个GT Bounding box里面，不在就是负样本，也就是 $c_{x, y}^{*} = 0$ ；如果在一个或多个box里面，则根据FPN不同层级feature map 能够回归的范围阈值筛除不符合条件的box，然后继续重复上述步骤判断该特征点是否有意义（ $c_{x, y}^{*} > 0$ ）。

center-ness的损失：BCE损失（二值交叉熵），我很奇怪，这部分并没有体现在上面那个公式里面，不过肯定是有的。

7. 补充一些细节

在引入FPN的同时还引入一些改变，仔细看看下一段英文引用，我简单翻译下，根据论文[14]、[15]（FPN、Focal loss），FCOS在不同的特征层级之间共享head（共享的是结构/权重共享，代码中详看 cls_tower和bbox_tower ）。但是不同的特征层级需要回归不同的大小范围（例如，P3的大小范围是[0，64]，P4的大小范围是[64，128]，因此对于不同的特征层级使用相同的head是不合理的。因此，论文中不再使用标准的exp(x)，而是使用exp( $s_{i}$ * x)，其中可训练标量 $s_{i}$ 被用来自动调整不同层级特征的指数函数的基数，从而稍微提高了检测性能（在下面代码中si首次出现在__init__()函数的最后）。推荐你们仔细看看下面的代码和注释，注释主题来自于这篇FCOS代码解析，其中部分是我补充和修改的。

Finally, following [14, 15], we share the heads between different feature levels, not only making the detector parameter-efficient but also improving the detection performance. However, we observe that different feature levels are required to regress different size range (e.g., the size range is [0, 64] for P3 and [64, 128] for P4), and therefore it is not reasonable to make use of identical heads for different feature levels. As a result, instead of using the standard exp(x), we make use of exp(six) with a trainable scalar si to automatically adjust the base of the exponential function for feature level Pi , which slightly improves the detection performance.

class FCOSHead(torch.nn.Module):
    def __init__(self, cfg, in_channels):
        """
        Arguments:
            in_channels (int): number of channels of the input feature
            fpn每层的输出通道数，这里也许真的是为了共享权重所以输出通道数目都一样，如256
        """
        super(FCOSHead, self).__init__()
        # TODO: Implement the sigmoid version first.
        num_classes = cfg.MODEL.FCOS.NUM_CLASSES - 1              # eg:80
        self.fpn_strides = cfg.MODEL.FCOS.FPN_STRIDES             # eg:[8, 16, 32, 64, 128]
        self.norm_reg_targets = cfg.MODEL.FCOS.NORM_REG_TARGETS   # eg:False 直接回归还是归一化后回归
        self.centerness_on_reg = cfg.MODEL.FCOS.CENTERNESS_ON_REG # eg:False centerness和哪个分支共用特征
        self.use_dcn_in_tower = cfg.MODEL.FCOS.USE_DCN_IN_TOWER   # eg:False 可形变卷积

        cls_tower = []
        bbox_tower = []
        # eg: cfg.MODEL.FCOS.NUM_CONVS=4头部共享特征时(也称作tower)有4层卷积层
        for i in range(cfg.MODEL.FCOS.NUM_CONVS):
            if self.use_dcn_in_tower and 
                    i == cfg.MODEL.FCOS.NUM_CONVS - 1:
                conv_func = DFConv2d
            else:
                conv_func = nn.Conv2d

            # cls_tower和bbox_tower都是4层的256通道的3×3的卷积层，后加一些GN和Relu
            # ！注意这里也是共享的部分，对应forward看，FPN输出的每一层级特征都经过同样的cls_tower和bbox_tower
            cls_tower.append(
                conv_func(
                    in_channels,
                    in_channels,
                    kernel_size=3,
                    stride=1,
                    padding=1,
                    bias=True
                )
            )
            cls_tower.append(nn.GroupNorm(32, in_channels))
            cls_tower.append(nn.ReLU())
            bbox_tower.append(
                conv_func(
                    in_channels,
                    in_channels,
                    kernel_size=3,
                    stride=1,
                    padding=1,
                    bias=True
                )
            )
            bbox_tower.append(nn.GroupNorm(32, in_channels))
            bbox_tower.append(nn.ReLU())

        self.add_module('cls_tower', nn.Sequential(*cls_tower))
        self.add_module('bbox_tower', nn.Sequential(*bbox_tower))
        
        # 下面连续 3 个部分也就是head的输出，结果分析和3,4章节分析的一样
        # cls_logits就是网络的直接分类输出结果，shape:[H×W×C]
        self.cls_logits = nn.Conv2d(
            in_channels, num_classes, kernel_size=3, stride=1,
            padding=1
        )
        # bbox_pred就是网络的回归分支输出结果，shape:[H×W×4]
        self.bbox_pred = nn.Conv2d(
            in_channels, 4, kernel_size=3, stride=1,
            padding=1
        )
        # centerness就是网络抑制低质量框的分支，shape:[H×W×1]
        self.centerness = nn.Conv2d(
            in_channels, 1, kernel_size=3, stride=1,
            padding=1
        )

        # initialization 这些层里面的卷积参数都进行初始化
        for modules in [self.cls_tower, self.bbox_tower,
                        self.cls_logits, self.bbox_pred,
                        self.centerness]:
            for l in modules.modules():
                if isinstance(l, nn.Conv2d):
                    torch.nn.init.normal_(l.weight, std=0.01)
                    torch.nn.init.constant_(l.bias, 0)

        # initialize the bias for focal loss 我只知道分类是用focal loss，可能是一种经验trick?
        prior_prob = cfg.MODEL.FCOS.PRIOR_PROB
        bias_value = -math.log((1 - prior_prob) / prior_prob)
        torch.nn.init.constant_(self.cls_logits.bias, bias_value)

        # P3-P7共有5层特征FPN，缩放因子，对回归结果进行缩放
        # ！！这一部分就算是我们在本章节说的si
        self.scales = nn.ModuleList([Scale(init_value=1.0) for _ in range(5)])  

    def forward(self, x):
        logits = []
        bbox_reg = []
        centerness = []
        # x是fpn输出的各层级特征，你会发现每一层级的特征使用同一个cls_tower和bbox_tower，这可能就是论文中说的head共享参数，提升性能吧？
        for l, feature in enumerate(x):
            # 要注意，不图层经过tower之后的特征图大小是不一样的
            cls_tower = self.cls_tower(feature)
            box_tower = self.bbox_tower(feature)

            logits.append(self.cls_logits(cls_tower))
            # 根据centerness_on_reg选择对应的tower特征
            if self.centerness_on_reg:
                centerness.append(self.centerness(box_tower))
            else:
                centerness.append(self.centerness(cls_tower))

            # 通过bbox_pred(box_tower)得到H * W * 4的特征结果，然后再缩放，最终结果是要输入到回归步骤中来预测(l, r, t, d).
            bbox_pred = self.scales[l](self.bbox_pred(box_tower))  # 得到缩放后的bbox_pred
            # 默认False，如果是True，先归一化然后回归
            if self.norm_reg_targets:
                bbox_pred = F.relu(bbox_pred)
                if self.training:
                    bbox_reg.append(bbox_pred)
                else:
                    bbox_reg.append(bbox_pred * self.fpn_strides[l])
            else:
                # ????有个exp()，很玄学，下面继续讲
                bbox_reg.append(torch.exp(bbox_pred))
        return logits, bbox_reg, centerness

[14] Tsung-Yi Lin, Piotr Dollar, Ross Girshick, Kaiming He, ´ Bharath Hariharan, and Serge Belongie. Feature pyramid networks for object detection. In Proc. IEEE Conf. Comp. Vis. Patt. Recogn., pages 2117–2125, 2017.

[15] Tsung-Yi Lin, Priya Goyal, Ross Girshick, Kaiming He, and Piotr Dollar. Focal loss for dense object detection. In ´ Proc. IEEE Conf. Comp. Vis. Patt. Recogn., pages 2980–2988, 2017.

提一下两个点：

（1）引入 $s_{i}$ ：我看了下大佬的解释，anchor-base的模型预设置了不同尺寸和宽高比的anchor去适应训练集以及测试集中目标的尺寸，所以能够消除尺度不变性的影响，而anchor-free的模型没有设置anchor这一步必然存在尺度不变性问题，因此为了提高性能，模型引入 $s_{i}$ 达到尺度不变性的目标。

（2）承接代码段落最后那一块，为啥回归部分bbox_reg存在一个exp()函数（其实我也很懵。。），解释在下面。

Moreover, since the regression targets are always positive, we employ exp(x) to map any real number to (0, + $infty$ ) on the top of the regression branch

8. 实验结果与个人的一点心得

简单的看下就得了。。，红色部分展示了同样的backbone，FCOS确实有更好的效果，但是啊，为了进一步提升FCOS的性能，作者引入了更复杂的Backbone，以及各种各样的trick（比如GIOU）还有将center-ness分支并入回归分支这一类的实验，感觉相对于从传统one-stage目标检测模型在速度性能上可能差一些。

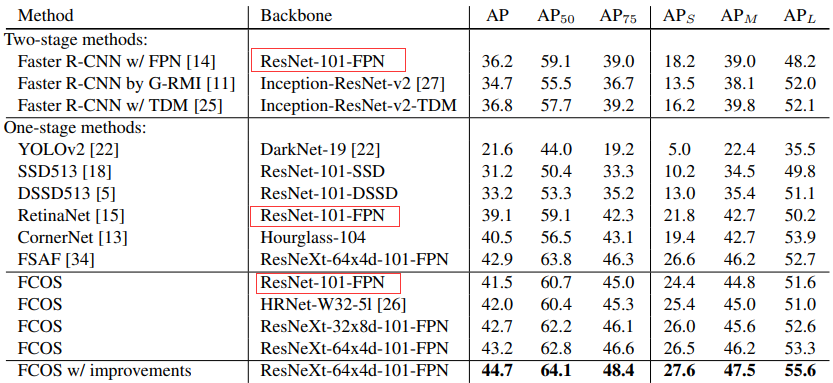
下图就是各种提升AP的trick，但总感觉速度回慢不少。

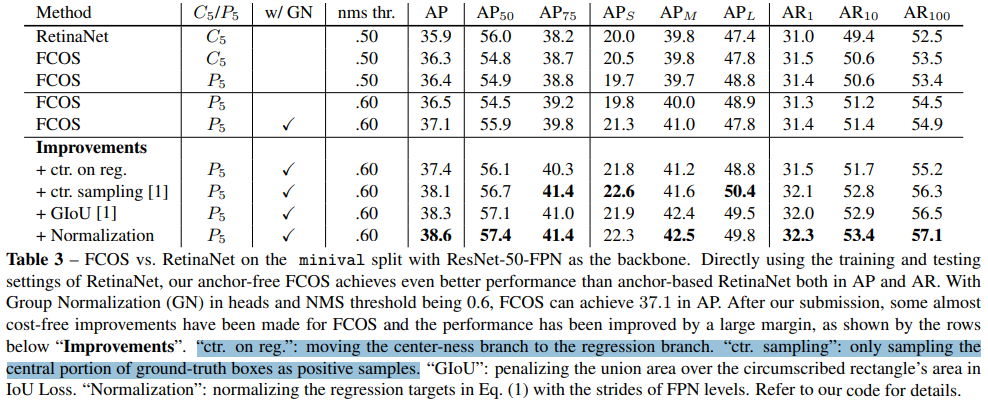
下图实验证明了，为传统classification_score加权求center-ness，并将两者相乘作为特征点的新的置信度是有意义的。简单解释一下，如右图所示，新置信度越高，它对应预测出来的box和GT Bounding box的IOU越高，这说明筛选后的预测box质量可以！可以发现新置信度和IOU成正比关系。

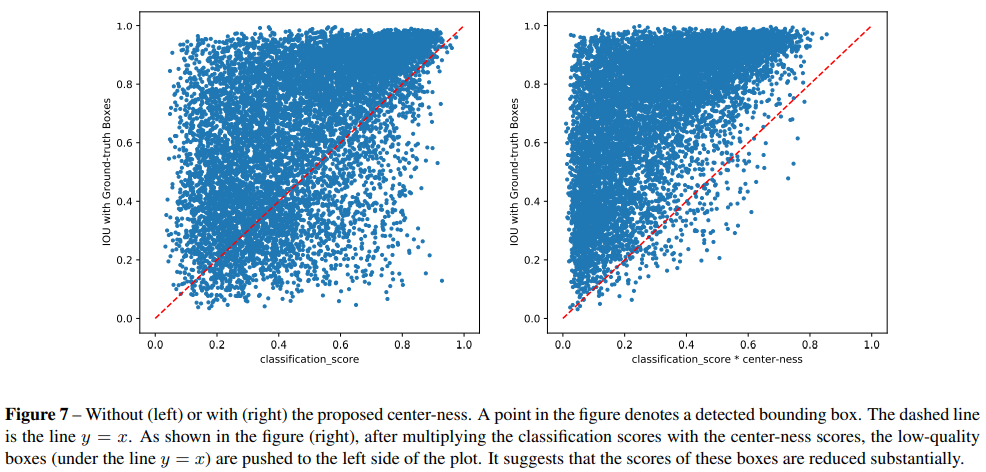
总的来说：

FCOS与许多基于FCN的思想是统一的，因此可以轻松引入那些提升性能的trick，例如FPN、GN、可形变卷积等等。
FCOS通过设置了很多巧妙的技巧（FPN，center-ness，各层特征点回归的尺度限制等）实现了proposal free和anchor free，避免了复杂的IOU计算以及训练期间 anchor 和GT Bounding box之间的匹配，但是这些设置可能更适应于某一特定类型的数据，笔者经过试验证明，如果使用一些和COCO或者ImageNet特征分布有差异的数据集来训练，FCOS的普适性就不是很好了。
FCOS可以替代传统 two-stage 模型中的RPN网络，其性能明显优于基于锚点的RPN算法（这一点挺好的。。虽然我没试验过，不过two-stage已经有点慢了，加上FCOS可能都不能在实际场景中应用）。
FCOS可以经过最小的修改便可扩展到其他的视觉任务，包括实例分割、关键点检测。