决策树最大的优点是它的过程完全符合人的思考习惯：分门别类，逐步深入。

1 决策树的历史

决策树很有意思，基本上到了家喻户晓的程度，但是其起源、发展的脉络却一直没有一个很清晰的路径，我搜集了一些资料，整理如下：

• 1 关键人物：他们基本上代表了目前决策树发展（应用）的几大派系，值得注意的是，有两个华人也可以被列进来，骄傲一下。
  
• 2 发展的历史顺序
  • 1 1966年，CLS学习系统中就已经提出决策树算法的概念。
  • 2 1979年，J.R Quinlan 给出ID3算法原型。
    • 信息增益，主要针对离散型属性数据
  • 3 1984年，L.Breiman,J.Friedman,R.Olshen和C.Stone于提出CART树。
    • Gini系数避免了信息增益产生的问题，过拟合问题，非常好的泛化能力，有很好的推广能力
  • 4 1993年，Quinlan发展了ID3算法，提出C4.5算法。
    • 信息增益率，增加对连续属性的离散化，避免ID3算法过度配适
  • 5 1993年，Quinlan发展了C4.5算法，提出C5.0算法。
    • 适用于处理大数据集，采用Boosting方式提高模型准确率，又称为BoostingTrees，在软件上计算速度比较快，占用的内存资源较少。
  • 6 1995年，L.Breiman,Adele Cutler提出随机森林，并注册商标。
  • 7 1999年，Friedman于提出GBDT，弱分类器为CART树。
  • 8 2008年，周志华提出孤立森林，适用于连续数据的无监督异常检测。
  • 9 2016年，陈天奇提出XGBOOST，优化了GBDT的效果
  • 10 2017年，微软提出LightGBM，改进XGBOOST的效率

从决策树算法（或者称树族算法）的发展来看非常有意思。第一，它的发展历史非常悠久，就算从1980年开始算起到现在也有超过40年的历史了。第二，有几个关键人物一直贯穿着始终（两个man, friedman, breiman)。第三，树的发展有“横向的”（随机森林）和“纵向的”（梯度提升）两个大方向，目前看来是纵向的树算法占了上风。

2 决策树的原理

关于决策树的原理，已经有很多不错的文章进行了介绍，我也就不再赘复；从技能角度上看，我觉得从代码的实现上会有更好的理解。
这里没有数学公式，只是简单做个小总结：

• 1 决策树从根节点出发，每次选取一个变量进行分叉
• 2 如果分叉的枝超过两个，就是多叉树（例如ID3）；如果只有两个枝那么就是二叉树(CART)
• 3 从某种程度上，用二叉树就够了，因为其形式更简单，效果上也可以和多叉树等效（想想二进制表达任何数字）
• 4 决策树根本原始就是通过不断的分叉（生长）把一个复杂问题分的比较细，从而帮助我们做出决策
• 5 生长的过程需要通过gini（或者mse)这样的指标来进行衡量，从而选出最好的分叉方式（这也是算法的核心问题）
• 6 如果是分类问题，一般使用gini；如果是回归问题，一般用mse

3 泰坦尼克号数据分析

上面已经把理论铺的差不多了，下面接着看泰坦尼克号的数据，再来张图撑场子

上一篇文章已经完成了数据的清洗，接下来可以对数据做一些分析。先看看变量间的关联：

colormap = plt.cm.viridis
plt.figure(figsize=(12,12))
plt.title('Pearson Correlation of Features', y=1.05, size=15)
sns.heatmap(train.astype(float).corr(),linewidths=0.1,vmax=1.0, square=True, cmap=colormap, linecolor='white', annot=True)

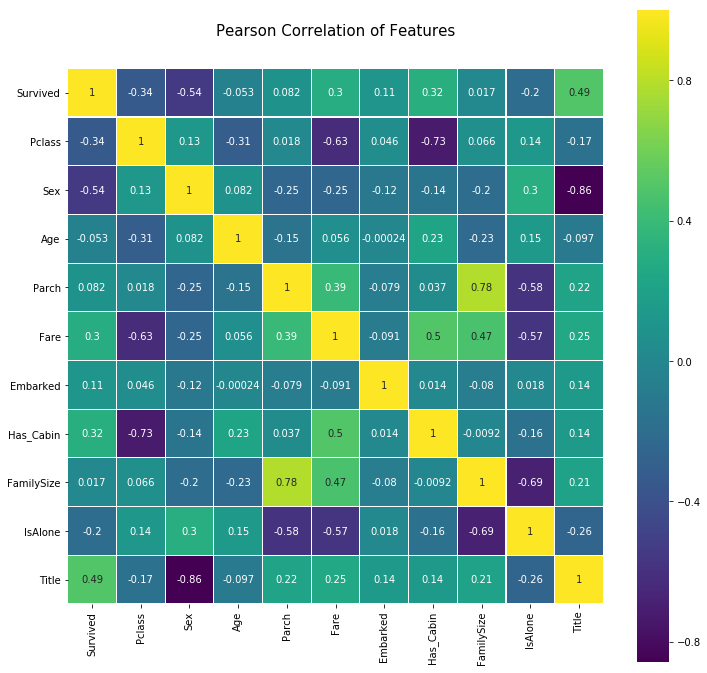
从相关分析来看（第一行），Sex和Title和与Survived(是否生存)的关联较强（-0.54， 0.49）

• Title & Survived

train[['Title', 'Survived']].groupby(['Title'], as_index=False).agg(['mean', 'count', 'sum'])
# Since "Survived" is a binary class (0 or 1), these metrics grouped by the Title feature represent:
    # MEAN: survival rate
    # COUNT: total observations
    # SUM: people survived
# title_mapping = {"Mr": 1, "Miss": 2, "Mrs": 3, "Master": 4, "Rare": 5} 

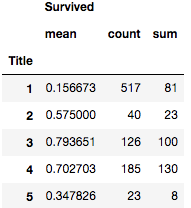
看起来Title为3(Mrs)，4(Master)两类的生存率比较高（但别忘记，Title是我们衍生出来的），我们再看看性别。

• Sex & Survived

train[['Sex', 'Survived']].groupby(['Sex'], as_index=False).agg(['mean', 'count', 'sum'])
# Since Survived is a binary feature, this metrics grouped by the Sex feature represent:
    # MEAN: survival rate
    # COUNT: total observations
    # SUM: people survived
    
# sex_mapping = {{'female': 0, 'male': 1}} 

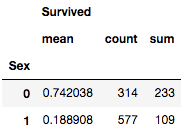
两个小结论：

• Mr（15.7%） 比 male(18.9%)要低
• Title似乎比Sex要更强一些，这是因为Title包含了Sex信息

我们从原始数据来分析一下Title和Sex的关系：

# Let's use our 'original_train' dataframe to check the sex distribution for each title.
# We use copy() again to prevent modifications in out original_train dataset
title_and_sex = df.copy()[['Name', 'Sex']]

# Create 'Title' feature
title_and_sex['Title'] = title_and_sex['Name'].apply(get_title)

# Map 'Sex' as binary feature
title_and_sex['Sex'] = title_and_sex['Sex'].map( {'female': 0, 'male': 1} ).astype(int)

# Table with 'Sex' distribution grouped by 'Title'
title_and_sex[['Title', 'Sex']].groupby(['Title'], as_index=False).agg(['mean', 'count', 'sum'])

# Since Sex is a binary feature, this metrics grouped by the Title feature represent:
    # MEAN: percentage of men
    # COUNT: total observations
    # SUM: number of men

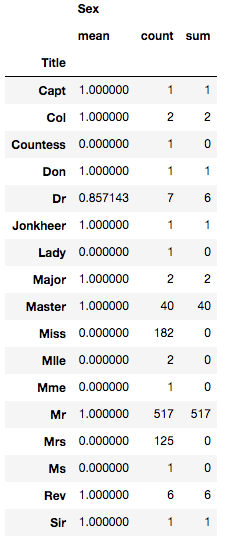
因为Sex是使用0， 1表示的，所以看均值，如果是为0或者为1，那么这个Title就是和性别完全挂钩的。
我们发现，除了一个例外（女博士 Dr，是罗斯吗？）,其他的Title都是纯性别的。从信息的角度上，Title由于Sex。

4 开始决策树

从上面的分析我们有了一些感觉，现在怎么利用这些分析结果呢？或者说怎样和决策树挂上钩呢？
我们先来看决策树的一个关键指标（gini不纯度）。

基尼不纯度：将来自集合中的某种结果随机应用于集合中某一数据项的预期误差率。

IG = Σ????????(1−????????)=Σ????????−Σ????2????=1−∑????2????
IG = ????0×(1−????0)+????1×(1−????1)=????0+????1−????20−????21=1−(????20+????21)
简言之，将对错概率交叉相乘
原版的函数如下：

# 原版的Gini不纯度计算
def get_gini_impurity(survived_count, total_count):
    survival_prob = survived_count / total_count
    not_survival_prob = 1 - survival_prob

    random_observation_survived_prob = survival_prob 
    random_observation_not_surviced_prob = 1 - random_observation_survived_prob

    mislabelling_survived_prob = not_survival_prob * random_observation_survived_prob
    mislabelling_not_survived_prob = survival_prob * random_observation_not_surviced_prob

    gini_impurity = mislabelling_survived_prob + mislabelling_not_survived_prob

    return gini_impurity

我觉得印度小哥的表达有点绕了，所以做如下改动（后面会验证是等效的）：

# 我的Gini不纯度计算
def get_gini_impurity_simple(target_count, total_count):
    p1 = target_count /  total_count
    p0 =  1 - p1 
    return 1 - p1**2 - p0**2

接下来先从第一个分叉节点开始（第一步的决策），先计算当前数据集的初始Gini不纯度

train.Survived.value_counts()

先对目标变量计算，得到死亡和幸存的人数。

# Gini Impurity of starting node
gini_impurity_starting_node = get_gini_impurity(342, 891)
gini_impurity_starting_node
# 结果 0.47301295786144265

# 测试一下自定义的gini
get_gini_impurity_simple(342, 891)
# 0.47301295786144276

OK， 结果是等效的，不过看起来我的函数简单多了对不？
接下来我们要进行决策了，使用哪个变量呢？
如果使用Sex进行决策：

train.groupby(['Sex', 'Survived']).size().unstack()

# 男性
# Gini Impurity decrease of node for 'male' observations
gini_impurity_men = get_gini_impurity(109, 577)
gini_impurity_men
# 0.3064437162277843

# 女性
# Gini Impurity decrease if node splited for 'female' observations
gini_impurity_women = get_gini_impurity(233, 314)
gini_impurity_women
# 0.3828350034484158

分别计算了性别的gini不纯度后，需要进行加权。

# 性别加权的情况
# Gini Impurity decrease if node splited by Sex
men_weight = 577/891
women_weight = 314/891
weighted_gini_impurity_sex_split = (gini_impurity_men * men_weight) + (gini_impurity_women * women_weight)
weighted_gini_impurity_sex_split
# 0.3333650003885905

既然说是“不纯度”，这个指标当然是越小越好了。我们看看如果用性别区分后，这个指标的改善程度。

# 使用性别划分达到的基尼增益
sex_gini_decrease = weighted_gini_impurity_sex_split - gini_impurity_starting_node
sex_gini_decrease
# -0.13964795747285214

改进了大约0.14。我们前面分析过，Title的信息比Sex更多，那么使用Title应该会更好，我们试一试

train.groupby(['Title', 'Survived']).size().unstack()

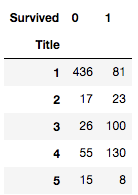
一般来说，能分的更细的变量一般信息量都更大；但是也会造成不稳定，所以要再变量的分割粒度上取一个平衡。（少于10类的一般问题都不大）

# 因为类别不均衡，使用1或非1计算
# Gini Impurity decrease of node for observations with Title == 1 == Mr
gini_impurity_title_1 = get_gini_impurity(81, 517)
gini_impurity_title_1
# 0.26425329886377663
# Gini Impurity decrease if node splited for observations with Title != 1 != Mr
gini_impurity_title_others = get_gini_impurity(261, 374)
gini_impurity_title_others
# 0.42170207898424317
# Title的加权平均
# Gini Impurity decrease if node splited for observations with Title == 1 == Mr
title_1_weight = 517/891
title_others_weight = 374/891
weighted_gini_impurity_title_split = (gini_impurity_title_1 * title_1_weight) + (gini_impurity_title_others * title_others_weight)
weighted_gini_impurity_title_split
# 0.3303429102723675

title_gini_decrease = weighted_gini_impurity_title_split - gini_impurity_starting_node
title_gini_decrease
# -0.14267004758907514

计算Title的步骤和Sex是一样的，可以看到其改进程度大于Sex（0.142 > 0.139),所以使用Title分割（或者做决策）是一个更好的选择。

下面一段代码用于暴力测试，看看决策树生长到第几层比较好。

cv = KFold(n_splits=10)            # Desired number of Cross Validation folds
accuracies = list()
max_attributes = len(list(train))
depth_range = range(1, max_attributes + 1)

# Testing max_depths from 1 to max attributes
# Uncomment prints for details about each Cross Validation pass
for depth in depth_range:
    fold_accuracy = []
    tree_model = tree.DecisionTreeClassifier(max_depth = depth)
    # print("Current max depth: ", depth, "n")
    for train_fold, valid_fold in cv.split(train):
        f_train = train.loc[train_fold] # Extract train data with cv indices
        f_valid = train.loc[valid_fold] # Extract valid data with cv indices

        model = tree_model.fit(X = f_train.drop(['Survived'], axis=1), 
                               y = f_train["Survived"]) # We fit the model with the fold train data
        valid_acc = model.score(X = f_valid.drop(['Survived'], axis=1), 
                                y = f_valid["Survived"])# We calculate accuracy with the fold validation data
        fold_accuracy.append(valid_acc)

    avg = sum(fold_accuracy)/len(fold_accuracy)
    accuracies.append(avg)
    # print("Accuracy per fold: ", fold_accuracy, "n")
    # print("Average accuracy: ", avg)
    # print("n")
    
# Just to show results conveniently
res_df = pd.DataFrame({"Max Depth": depth_range, "Average Accuracy": accuracies})
res_df = res_df[["Max Depth", "Average Accuracy"]]
print(res_df.to_string(index=False))

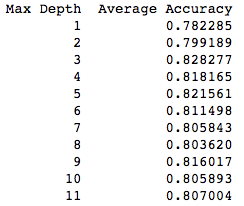
通过Kfold测试，知道树的深度为3是最好的。而给到太多的层数可能导致了过拟合
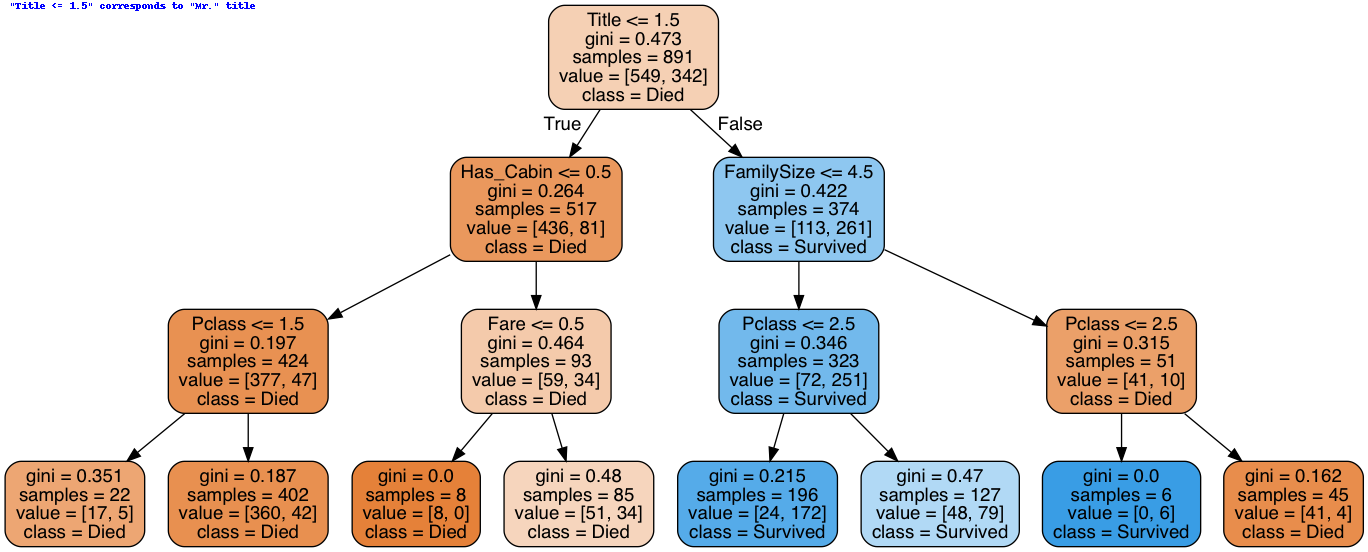
最后我们使用Sklearn生成最终的决策树，并生成树状图。

y_train = train['Survived']
x_train = train.drop(['Survived'], axis=1).values 


# Create Decision Tree with max_depth = 3
decision_tree = tree.DecisionTreeClassifier(max_depth = 3)
decision_tree.fit(x_train, y_train)


from sklearn import tree
# Export our trained model as a .dot file
with open("tree1.dot", 'w') as f:
     f = tree.export_graphviz(decision_tree,
                              out_file=f,
                              max_depth = 3,
                              impurity = True,
                              feature_names = list(train.drop(['Survived'], axis=1)),
                              class_names = ['Died', 'Survived'],
                              rounded = True,
                              filled= True )
                              
from subprocess import check_call
#Convert .dot to .png to allow display in web notebook
check_call(['dot','-Tpng','tree1.dot','-o','tree1.png'])

# Annotating chart with PIL
img = Image.open("tree1.png")
draw = ImageDraw.Draw(img)

draw.text((10, 0), # Drawing offset (position)
          '"Title <= 1.5" corresponds to "Mr." title', # Text to draw
          (0,0,255) # RGB desired color
          ) # ImageFont object with desired font
img.save('sample-out.png')
PImage("sample-out.png")

# Code to check available fonts and respective paths
# import matplotlib.font_manager
# matplotlib.font_manager.findSystemFonts(fontpaths=None, fontext='ttf')

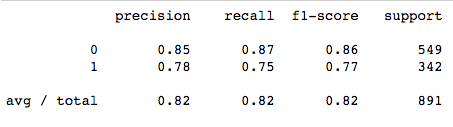
计算一下指标，后续和我自己做的树可以比较一下：

acc_decision_tree = round(decision_tree.score(x_train, y_train) * 100, 2)
acc_decision_tree
# 82.38

from sklearn.metrics import classification_report
print(classification_report(y_train,decision_tree.predict(x_train)))

到这里决策树就建完了，没什么算法的感觉，就是套了一下公式。
下一篇我会介绍我建的决策树类，先看整体的结构，运行方式。在这之后我会继续把里面用到的每一个函数都拆解开来说。

最后

以上就是花痴皮卡丘为你收集整理的Python实现决策树（系列文章3）-- 从数据分析到决策树1 决策树的历史2 决策树的原理3 泰坦尼克号数据分析4 开始决策树的全部内容，希望文章能够帮你解决Python实现决策树（系列文章3）-- 从数据分析到决策树1 决策树的历史2 决策树的原理3 泰坦尼克号数据分析4 开始决策树所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。