递归与分治算法求集合划分问题

56 阅读 0 评论 37 点赞

我是靠谱客的博主文静大地，最近开发中收集的这篇文章主要介绍递归与分治算法求集合划分问题，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

二分搜索问题：

设：a[0:n-1]是一个已排好序的数组。请改写二分搜索算法，使得当搜索元素x不在数组中时，返回小于x的最大元素的位置I和大于x的最小元素位置J。当搜索元素在数组中时，I和J相同，均为x在数组中的位置。

参考函数原型：bool BinarySearch(int a[], int n, int x, int& i, int& j);

#include<iostream>
using namespace std;
#include<stdio.h>

bool BinarySearch(int a[], int n, int x, int& i, int& j) {
	int left = 0, mid, right = n - 1;
	while (left <= right) {
		mid = (left + right) / 2;
		if (x == a[mid]) {
			i = j = mid;
			return true;
		}
		if (x > a[mid])
			left = mid + 1;
		else
			right = mid - 1;
	}
	i = right;
	j = left;

	return false;
}

int main() {
	int x, i, j;
	int a[] = { 1,3,5,7,10,14,16,18,21,23,28 };
	cout << "原始数据为：" << endl;
	for (int i = 0; i < 11; i++) {
		cout << a[i] << " ";
	}
	cout << endl << "请输入待查数据：";
	cin >> x;
	if (BinarySearch(a, 11, x, i, j))
	{
		cout << "find the value at:" << i ;
	}
	else
	{
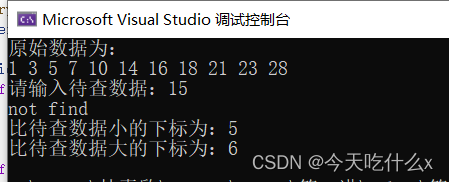
		cout << "not find" << endl;
		cout << "比待查数据小的下标为：" << i << endl;
		cout << "比待查数据大的下标为：" << j << endl;
	}
}

集合划分问题：

问题描述

n个元素的集合{1, 2, …, n}可以划分为若干个非空子集。例如，当n=4 时，集合{1，2，3，4}可以划分为15 个不同的非空子集如下：

{{1}，{2}，{3}，{4}}，{{1，2}，{3}，{4}}，{{1，3}，{2}，{4}}，

{{1，4}，{2}，{3}}，{{2，3}，{1}，{4}}，{{2，4}，{1}，{3}}，

{{3，4}，{1}，{2}}，{{1，2}，{3，4}}，{{1，3}，{2，4}}，

{{1，4}，{2，3}}，{{1，2，3}，{4}}，{{1，2，4}，{3}}，

{{1，3，4}，{2}}，{{2，3，4}，{1}}，{{1，2，3，4}}

其中，集合{{1，2，3，4}}由1 个子集组成；集合{{1，2}，{3，4}}，{{1，3}，{2，4}}，{{1，4}，{2，3}}，{{1，2，3}，{4}}，{{1，2，4}，{3}}，{{1，3，4}，{2}}，{{2，3，4}，{1}}由2 个子集组成；集合{{1，2}，{3}，{4}}，{{1，3}，{2}，{4}}，{{1，4}，{2}，{3}}，{{2，3}，{1}，{4}}，{{2，4}，{1}，{3}}，{{3，4}，{1}，{2}}由3 个子集组成；集合{{1}，{2}，{3}，{4}}由4 个子集组成。

你的任务：给定正整数n 和m，计算出n 个元素的集合{1, 2, …, n}可以划分为多少个不同的由m个非空子集组成的集合。

输入

有若干行，每行2个整数n、m，分别是元素个数和非空子集数，n£100。

输出

对每一行输入数据n、m，输出集合{1, 2, …, n}的不同的由m个非空子集组成的集合数。

输入样例

4 3

7 4

输出样例

6

350

#include <iostream>
#include<stdio.h>
using namespace std;

int f(int n, int m) {
	if (m == 1 || m == n) {
		return 1;
	}
	else {
		return f(n - 1, m - 1) + m * f(n - 1, m);
	}
}

int main() {
	int n;
	int count = 0;
	while (true) {
		cout << "请输入集合的元素个数：" << endl;
		cin >> n;
		if (n < 0) {
			break;
		}
		else {
			for (int i = 1; i <= n; i++) {
				int item = f(n, i);
				cout << "f(n," << i << ")=" << item << endl;
				count += item;
			}
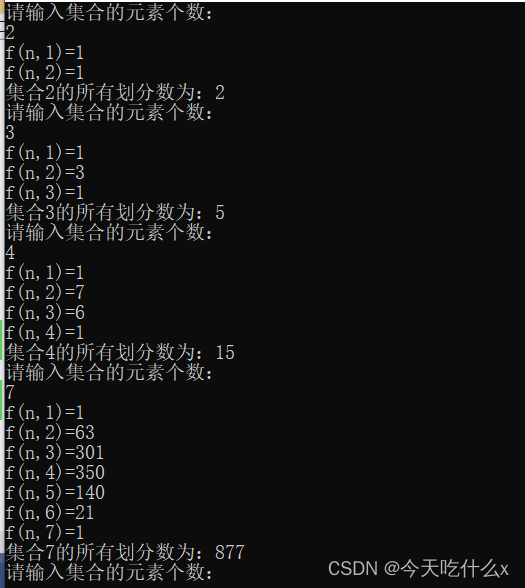
			cout << "集合" << n << "的所有划分数为：" << count;
          	count = 0;
		}
	}
	return 0;
}