前言

本文主要提到的是闭环形式状态观测器中的全维状态观测器，建议有时间可以阅读上一篇开环形式的状态观测器(篇幅不长)以理解状态观测器。

一、全维状态观测器

　　全维状态观测器是闭环状态观测器的一种。还是从非常常见的公式开始：

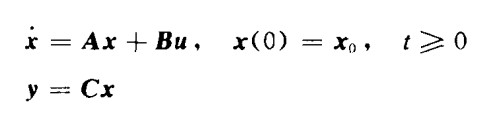
　　所谓全维状态观测器，就是以y和u为输出，且其状态变量与原系统状态变量满足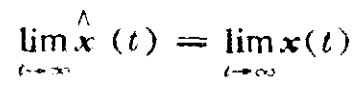
　　这很容易理解，就是我的模拟系统的输出最终与原系统的输出是一样的，这样模拟系统就完成了任务。
　　可以看到，全维状态观测器有两个输入，与开环形式的相比多了一个原系统的输出y,那这个y是干啥的，就是来构成闭环反馈的，也就是有了这个y的作用，我们可以修改系统矩阵的特征值，解决在开环状态反馈中解决不了的问题。
　　但在全维状态观测器中，作用到反馈回路中的不仅仅原系统的输出y，实际上，作为反馈量的是原系统与模拟系统的差值，经增益矩阵L反馈到模拟系统的积分器输入端构成一个闭环系统。
　　因此，这个时候，模拟系统被重构了，公式变成了
　　　　　$\dot{\hat{x}}=A\hat{x}+Bu+L(y-\hat{y})$
由于　　　　　　　$\hat{y}=C\hat{x}$
上式进一步变成
　　　　$\dot{\hat{x}}=(A-LC)\hat{x}+Bu+Ly$　　　（1）
其中待确定的系数矩阵只有L。
　　而且，在这个方程中$u$和$y$是输入，$(A-LC)$是系统矩阵，跟之前所说的全维观测器的定义相符。
　　言归正传，我们设计全维观测器的目的是为了观测状态变量，观测状态变量的方法是创建了一个跟原系统一样维度的观测器来模拟那些状态变量，模拟的最终目的就是要原系统的状态变量与模拟系统的状态变量的差值为0，即　　　　　　　$\dot{\tilde{x}}=(\dot{x}-\dot{\hat{x}})$
可得方程
　　　　　　$\dot{\tilde{x}}=(A-LC)\tilde{x}$　　　　（2）
　　这个方程表明，不管初始的误差${\tilde{x}}_0$有多大，只要让$(A-LC)$的特征值均具有负的实部，就可以让误差值最终变为0。
　　因为L是未确定的矩阵，因此可以将(A-LC)配置到合适的极点位置上，这就是极点配置的问题了。这里还有一个可任意配置极点的条件，其中只要{A，C}是能观测的，就能够证明得到可以任意配置极点。
总之，全维状态观测器的设计相对也比较简单：
（1） 要清楚反馈，是谁反馈回来，就能写出反馈后的状态方程即公式（1）；
（2） 要明确是要让谁最终趋于0，用原系统的状态方程减去模拟系统的状态方程就可以得到公式（2）；
（3）得到公式（2）就知道要对谁的极点进行配置，配置完成之后得到的就是矩阵L；
（4）得到矩阵L之后代入方程(1)就得到了全维状态观测器的状态方程。

参考书籍 线性控制理论 阙志宏

最后

以上就是灵巧月光为你收集整理的【状态观测器】全维状态观测器前言一、全维状态观测器的全部内容，希望文章能够帮你解决【状态观测器】全维状态观测器前言一、全维状态观测器所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。