1 前言

  前面已经讲解了滑膜观测器的原理，推导以及搭建，接下来再来介绍另外一个极具代表性的观测器，那就是传说中的扩展卡尔曼滤波观测器，即EKF观测器。顾名思义，是个内藏扩展卡尔曼滤波器的状态观测器。

  首先单看扩展卡尔曼滤波器，众所周知，卡尔曼滤波器是一个及其常用的滤波器，而这里叫扩展卡尔曼滤波，这里的“扩展”体现在哪里呢?

  据说是因为卡尔曼滤波是给线性系统使用的，而扩展卡尔曼则是作了升级，让其也能适用于非线性系统，而电机系统是个巨复杂，非线性，强耦合的系统，那自然就得用适用于非线性系统的扩展卡尔曼滤波。扩展卡尔曼滤波相比较于卡尔曼滤波，其实只是多了一个使用泰勒展开的方式让系统传递函数线性化的过程。

  而扩展卡尔曼滤波观测器既然内置扩展卡尔曼滤波器，那就说明了这个观测器自带滤波功能。除此之外，扩展卡尔曼自带自我调节属性，是个自适应系统，性能优异。总之，相比较SMO的简单粗暴，EKF观测器则温柔细致，我愿称之为观测器中的开挂王。

  注：因为卡尔曼滤波以及扩展卡尔曼滤波牵扯到了很复杂很复杂的概念，没有非常好的数学基础理解起来那是非常非常吃力的，所以在这篇文章里我只会用尽可能通俗易懂的方式告诉大家扩展卡尔曼滤波是一个怎样的一个过程或者它到底在干什么，而不会一步一步的推导卡尔曼，只会让大家怎样去用它而不是教大家怎样把卡尔曼给证明，不然的话就是写它个几千字可能都讲不清楚。想学理论推导的同学可以去参考网上其他的一些优质文章或者视频教学。

2 卡尔曼滤波的原理

2.1 卡尔曼滤波的思想

  先给大家讲个小故事：
————————————————————————————————
  一辆配备高级雷达的自动驾驶的小车车正在以速度v=1m/s的速度朝着一堵墙快速前进，而它距离墙的距离10m。 经过5s的紧张行驶后，不出意外的话，小车车自己可以通过计算（10m-1m/s*5s）估算出那个时候的距离为5m，但是这个时候它开始怀疑自己，非要使用高级雷达测一下自己离墙还有多久，这一测，卧槽，测出来还有7m，我了嘞个嚓，一个5m，一个7m，怎么办，该信谁，如果选错了，刹车晚了，自己就车毁车亡了。

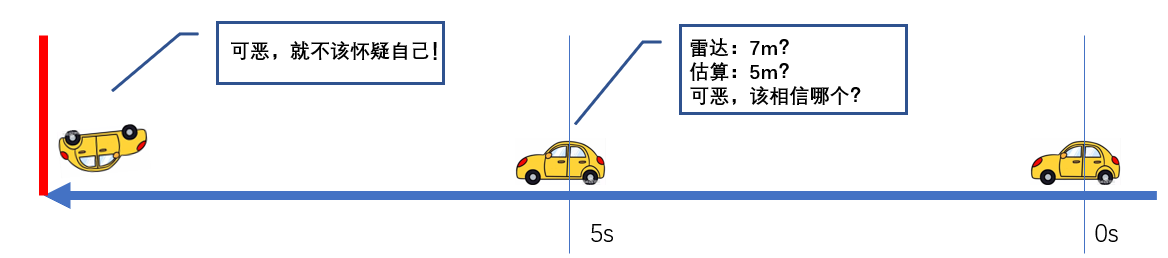
  小车车此时很纠结，内心开始纠结：
  相信自己吧，卧槽假如自己的速度没有5m/s，假如我的方向盘歪了，那可是高级雷达，嗯，得相信雷达，卧槽，假如雷达坏了，不准了。。。。。。

  这个时候有个人，姑且就叫他龙贝格吧（我乱起的啊），站了出来。

  龙贝格：“不管是估算的，还是测量的，肯定都有误差，你各自取一半不就好了，两者都相信，万无一失，所以就是(5 * 0.5 + 7 * 0.5)m。”
  小车车：“那如果雷达那边的误差更大一点怎么办？”
  龙贝格：“那就雷达取两成，自己估算的取8成，就是(5 * 0.8 + 7 * 0.2)m。”
  小车车：“那如果雷达准一点呢？”
  龙贝格：“你**有完没完，滚蛋。”

  这个时候又有一个人站了出来，姑且就叫他卡尔曼吧。

  卡尔曼：“你前面不是开了4s吗，那么你估算的值和雷达的观测值的数据记录都在吧，你可以根据前面的数据和结合误差参数做一些分析，最后决定在这个时候该信谁多一点就好了。”
  小车车：“咋分析？”
  卡尔曼：“秘密，不告诉你”。
  小车车：“狗贼，拿命来，可敢留下姓名。”
  卡尔曼：“天不生我卡尔曼，电控万古如长夜。”

  小车车最后还是没了。
—————————————————————————————————

  从这个故事中，我们可以了解到很多东西。如果站在雷达的角度上看，卡尔曼的思想就是为了让雷达的采样结果更加平滑，那就结合预估曲线来中和采样结果，实现滤波的作用；如果站在小车车的角度上看，卡尔曼的思想就是为了让小车车最终的预估结果更加准确，就结合雷达的观测结果来修正自己的预估值。另外卡尔曼还需要拥有一种可以随时调节预估值和观测值之间权重比的方法，而这权重比被称为卡尔曼增益。

  以上就是卡尔曼滤波的思想以及卡尔曼滤波要做的事情。

2.2 卡尔曼滤波的过程

  从上面小车车的故事中很显然的可以了解到，卡尔曼滤波的过程有三个步骤，第一预估，第二计算卡尔曼增益，第三结合观测值修正预估值。废话不多说，啪，直接贴出卡尔曼的这三步所用的公式：

  可能有些小伙伴就要开始暴躁起来了，卧槽，前一秒还是1+1，下一秒就是*******，不要着急，先混个脸熟，后面会讲怎么用这五个公式。

  又有人问了，这又是x，又是P的，这些字母代表的都是啥意思？不要着急，别管它代表啥意思，混个脸熟，后面会慢慢拨开它的嘴脸。

  说好的三步，怎么有5个式子？其中第1，3，4步很好理解，对应着卡尔曼的基本三步走内容，但是第2，5步在做什么？因为卡尔曼滤波法在计算卡尔曼增益的时候是利用了误差的正太分布以及协方差的特性，所以在这里需要计算一下误差协方差矩阵P，以此来计算出卡尔曼增益。

  这里可以提稍微一下为啥卡尔曼可以利用误差的协方差来计算卡尔曼增益（权重）或者说卡尔曼增益（权重）和误差的联系。再次回到小车车的故事，故事中，小车车最后估算结果不准确主要来源于方向盘不正，小车速度有偏差，这种来自于小车本身的因素被称为系统误差，而雷达测量的结果误差则来源于雷达本身，这种导致测量结果不准确的因素被称为观测误差，如果系统误差小，观测误差大，那估算值的权重自然就大一点，观测值的权重就小一点，反之类推，这是两者联系的本质原因。至于为啥要利用误差的协方差呢，这就牵扯到一个数学上的概率问题了，太深入的东西不讲，但是不可以不学哟。

  这就是卡尔曼滤波的全部过程了。

3 卡尔曼滤波和观测器的联系

  上面讲解了一下卡尔曼滤波的思想，那么它又是怎么和观测器结合在一起的呢？接下来，就要讲讲卡尔曼滤波与观测器之间的联系了。

3.1 观测器的引入

  首先列出观测器的示意图：

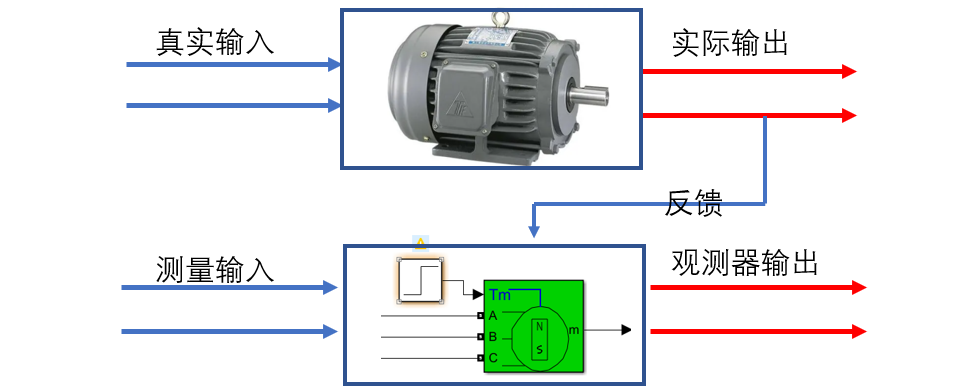
  这幅图大家很熟悉了，然后根据上图的模型，稍微加一下细节，直接摇身一变：

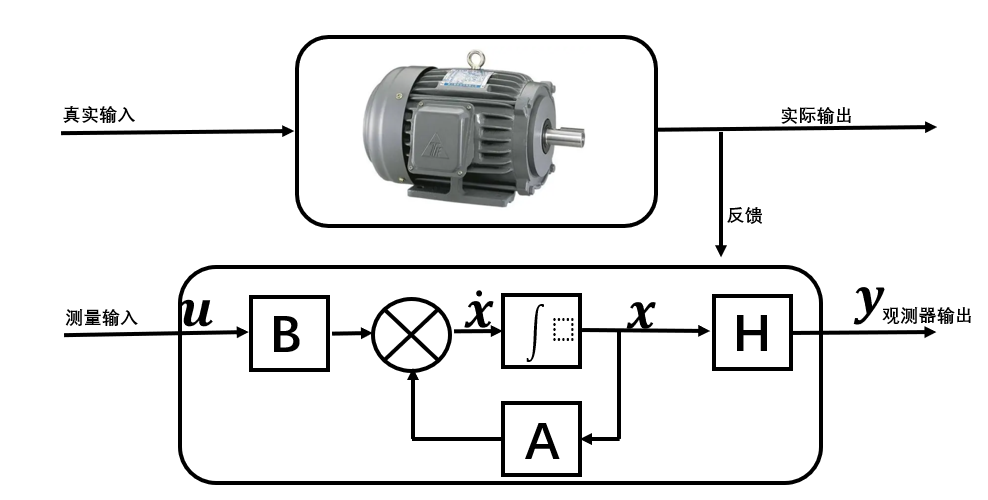
  可能有人开始卧槽了，这是个啥？这到底是个啥？我又是谁？不要着急，下面这个观测器的框架其实是在一门叫做《自动控制原理》的领域里提出来的，之前在讲SMO的时候，为啥没有引出这个观测器拓扑呢，是因为SMO的模型太简单了，不是特别依赖这个模型，而卡尔曼不行，必须完完全全依托这个模型。有人可能会提出，这个拓扑结构为啥要做成这样，这个东西只能意会不能言传，等你的深度累计到达一定程度的时候，自然而然就明白了。

  根据上图，可以非常清晰的列出一个线性系统的状态观测器模型的两个函数：

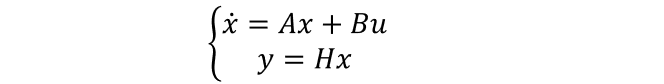
  其中$\dot{x}$为状态变量，$u$为输入，$y$为输出。 在这里就不给大家补习自控知识了，只要知道可以用这两个式子来代表一个线性系统的模型就好了。再回过头来看卡尔曼滤波的五个式子:

  可以发现，只要我们确定了系统的状态方程后，卡尔曼滤波的5个式子中，$z$是系统实际输出的观测值，除次之外，还有三个量无法确定，分别是F，Q，R，那么这三个量怎样去确定呢。首先Q代表的是系统误差，R代表的是观测误差，这个是由系统以及观测条件硬性决定的，所以是个常数，很好确定。

  另外再看F，可以看到卡尔曼滤波计算预估值的时候是使用上一个状态$x_{k-1}$来预估下一个状态$x_k$，而在观测器中的微分$\dot{x}$，在离散化系统中其定义为$\dot{x}=\frac{x_k-x_{k-1}}{\Delta t}$，所以有：

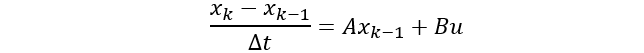
  化简得：

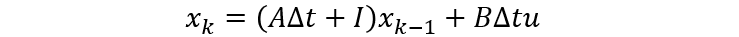
  现在这个形式是不是就跟卡尔曼滤波过程中的计算预估值形式一样了，F也可以确定了，即$F=(A\Delta t+I)$。

  立即推：只要将一个线性系统的状态方程搭建出来，就可以完整得走一遭卡尔曼滤波器的流程了。

3.2 卡尔曼滤波在观测器的体现

  东凑西凑终于可以将卡尔曼滤波器的流程完整的走一遭了，但是这个流程跟我观测器有什么关系呢？咱们观测器可是通过建立数学模型模拟真实系统，然后结合反馈修正模型，最后让观测器模型更加完美，你这个顶多就是花里胡哨走一波，感觉啥也没干。非也非也。

  再回到小车车的故事里，由于小车车怀疑自己的计算结果，此为预估值，后来它结合了雷达的测量结果，此为观测值，修正了一下自己的计算结果然后输出最终的结果。如果将小车车比作一个系统，小车车预估值就相当于观测器的输出，而雷达观测值即为真实系统的输出反馈，利用反馈来修正观测器，这难道不正好满足状态观测器的定义吗？

  下面再来看卡尔曼滤波流程中核心的一步，如下：

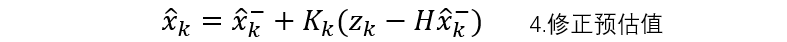
  其中$y=Hx$,为状态观测器的输出，$z$为系统实际输出的观测值，则$z-y$即为反馈error，而$K$为卡尔曼增益，再加上观测误差和系统误差，卡尔曼观测器的框图就变成了：

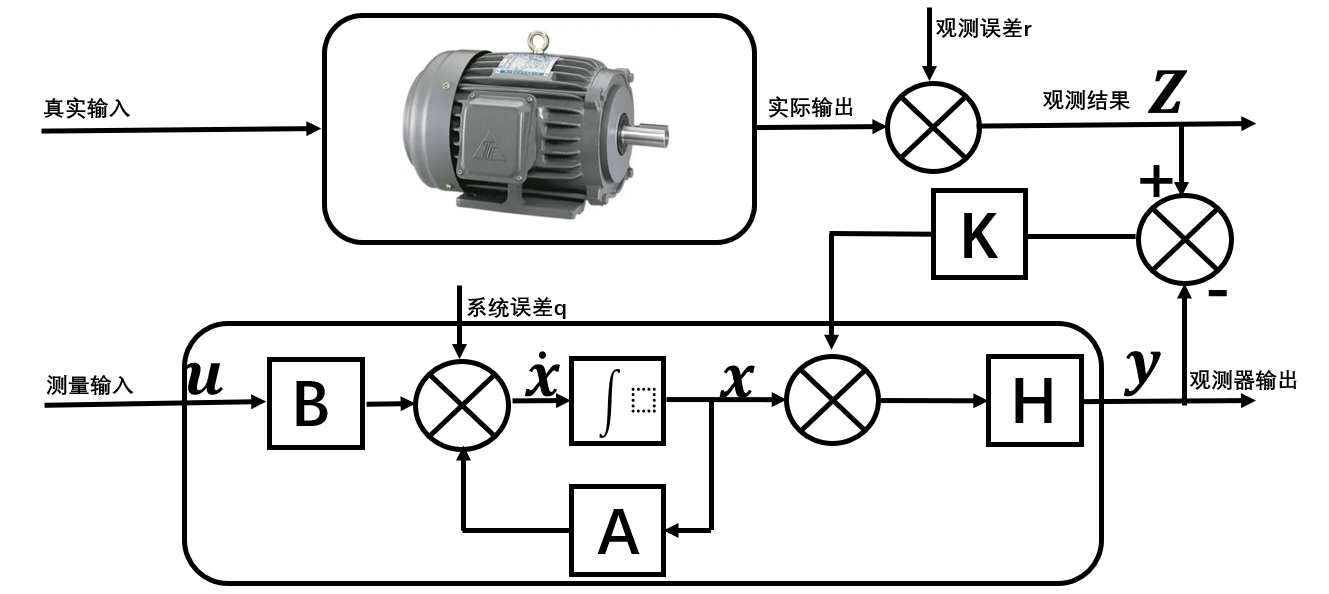
  现在就非常清楚卡尔曼在观测器中充当了什么样的角色，这样来看的话，就变得非常非常简单了，观测器和卡尔曼完美的结合在了一起。最后即可得出，卡尔曼观测器的工作原理就是通过观测器的输出和系统的实际输出之差再乘上一个卡尔曼增益K作为观测器的修正值，来修正状态观测器的状态量。同时还根据误差协方差自适应调节卡尔曼增益K。

4 扩展卡尔曼观测器的诞生

  下面再来讨论最后一个问题，前面花里胡哨一大堆，都有一个非常致命的缺陷，上面所有的理论都建立在这个系统必须是一个线性系统，但是对于大部分的系统，都是一个非线性系统，比如我们的目标电机系统，那该怎么办，所以扩展卡尔曼就站出来了，扩展卡尔曼有一个非常重要的过程，那就是线性化，让一个非线性系统同样适用卡尔曼滤波的过程，那么怎样线性化？

  这就得引出数学界最伟大的公式，泰勒公式。它是一个用函数在某点的信息描述其附近取值的公式。如果函数满足一定的条件，泰勒公式可以用函数在某一点的各阶导数值做系数构建一个多项式来近似表达这个函数。泰勒展开就是扩展卡尔曼线性化的凭证。

  至此，扩展卡尔曼观测器的解析就介绍完毕了。

END

最后

以上就是妩媚板栗为你收集整理的小猫爪：PMSM之FOC控制12-扩展卡尔曼滤波状态观测器解析1 前言2 卡尔曼滤波的原理3 卡尔曼滤波和观测器的联系4 扩展卡尔曼观测器的诞生END的全部内容，希望文章能够帮你解决小猫爪：PMSM之FOC控制12-扩展卡尔曼滤波状态观测器解析1 前言2 卡尔曼滤波的原理3 卡尔曼滤波和观测器的联系4 扩展卡尔曼观测器的诞生END所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。